2019-05-09 16:57:58 +08:00
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# 杨辉三角
|
|
|
|
|
|
|
2019-11-14 11:00:28 +08:00
|
|
|
|

|
2019-05-09 16:57:58 +08:00
|
|
|
|
|
|
|
|
|
|
> 本文首发于公众号「五分钟学算法」,是[图解 LeetCode](https://github.com/MisterBooo/LeetCodeAnimation) 系列文章之一。
|
|
|
|
|
|
>
|
|
|
|
|
|
> 个人网站:[https://www.cxyxiaowu.com](https://www.cxyxiaowu.com)
|
|
|
|
|
|
>
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
杨辉三角应该是大家很早就接触到的一个数学知识,它有很多有趣的性质:
|
|
|
|
|
|
|
|
|
|
|
|
- 每个数字等于上一行的左右两个数字之和,即 *C(n+1,i) = C(n,i) + C(n,i-1)*
|
|
|
|
|
|
- 每行数字左右对称,由 1 开始逐渐变大
|
|
|
|
|
|
- 第 n 行的数字有 n 项
|
|
|
|
|
|
- 第 n 行的第 m 个数和第 n - m + 1 个数相等 ,为[组合数](https://baike.baidu.com/item/%E7%BB%84%E5%90%88%E6%95%B0)性质之一
|
|
|
|
|
|
- ( a + b )<sup>n</sup>的展开式中的各项[系数](https://baike.baidu.com/item/%E7%B3%BB%E6%95%B0)依次对应杨辉三角的第 ( n + 1 ) 行中的每一项
|
|
|
|
|
|
- 。。。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
## 杨辉三角
|
|
|
|
|
|
|
|
|
|
|
|
题目来源于 LeetCode 上第 118 号问题:杨辉三角。题目难度为 Easy,目前通过率为 61.8% 。
|
|
|
|
|
|
|
|
|
|
|
|
### 题目描述
|
|
|
|
|
|
|
|
|
|
|
|
给定一个非负整数 *numRows,*生成杨辉三角的前 *numRows* 行。
|
|
|
|
|
|
|
2019-11-14 11:00:28 +08:00
|
|
|
|
|
2019-05-09 16:57:58 +08:00
|
|
|
|
|
|
|
|
|
|
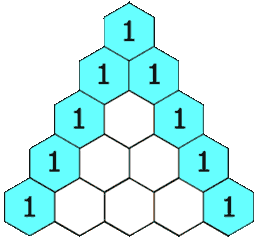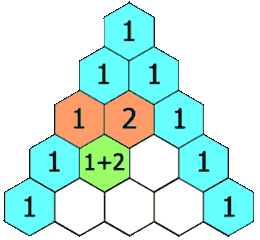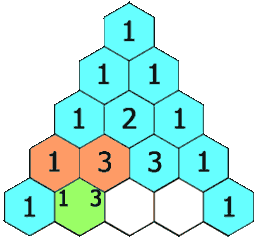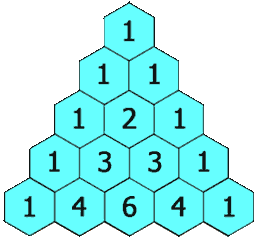
在杨辉三角中,每个数是它左上方和右上方的数的和。
|
|
|
|
|
|
|
|
|
|
|
|
**示例:**
|
|
|
|
|
|
|
|
|
|
|
|
```
|
|
|
|
|
|
输入: 5
|
|
|
|
|
|
输出:
|
|
|
|
|
|
[
|
|
|
|
|
|
[1],
|
|
|
|
|
|
[1,1],
|
|
|
|
|
|
[1,2,1],
|
|
|
|
|
|
[1,3,3,1],
|
|
|
|
|
|
[1,4,6,4,1]
|
|
|
|
|
|
]
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
### 题目解析
|
|
|
|
|
|
|
|
|
|
|
|
> 这道题目在各大高校的习题中经常出现。
|
|
|
|
|
|
|
|
|
|
|
|
对于本题而言,利用性质 1 :每一行的首个和结尾一个数字都是 1,从第三行开始,中间的每个数字都是上一行的左右两个数字之和。
|
|
|
|
|
|
|
|
|
|
|
|
### 代码实现
|
|
|
|
|
|
|
|
|
|
|
|
```java
|
|
|
|
|
|
class Solution {
|
|
|
|
|
|
public List<List<Integer>> generate(int numRows) {
|
|
|
|
|
|
|
|
|
|
|
|
List<List<Integer>> result = new ArrayList<>();
|
|
|
|
|
|
if (numRows < 1) return result;
|
|
|
|
|
|
|
|
|
|
|
|
for (int i = 0; i < numRows; ++i) {
|
|
|
|
|
|
//扩容
|
|
|
|
|
|
List<Integer> list = Arrays.asList(new Integer[i+1]);
|
|
|
|
|
|
list.set(0, 1); list.set(i, 1);
|
|
|
|
|
|
for (int j = 1; j < i; ++j) {
|
|
|
|
|
|
//等于上一行的左右两个数字之和
|
|
|
|
|
|
list.set(j, result.get(i-1).get(j-1) + result.get(i-1).get(j));
|
|
|
|
|
|
}
|
|
|
|
|
|
result.add(list);
|
|
|
|
|
|
}
|
|
|
|
|
|
return result;
|
|
|
|
|
|
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
## 杨辉三角II
|
|
|
|
|
|
|
|
|
|
|
|
题目来源于 LeetCode 上第 119 号问题:杨辉三角II。题目难度为 Easy,目前通过率为 55.5% 。
|
|
|
|
|
|
|
|
|
|
|
|
### 题目描述
|
|
|
|
|
|
|
|
|
|
|
|
给定一个非负索引 *k*,其中 *k* ≤ 33,返回杨辉三角的第 *k* 行。
|
|
|
|
|
|
|
2019-11-14 11:00:28 +08:00
|
|
|
|

|
2019-05-09 16:57:58 +08:00
|
|
|
|
|
|
|
|
|
|
在杨辉三角中,每个数是它左上方和右上方的数的和。
|
|
|
|
|
|
|
|
|
|
|
|
**示例:**
|
|
|
|
|
|
|
|
|
|
|
|
```
|
|
|
|
|
|
输入: 3
|
|
|
|
|
|
输出: [1,3,3,1]
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
**进阶:**
|
|
|
|
|
|
|
|
|
|
|
|
你可以优化你的算法到 *O*(*k*) 空间复杂度吗?
|
|
|
|
|
|
|
|
|
|
|
|
### 题目解析
|
|
|
|
|
|
|
|
|
|
|
|
这道题目的难点与思考点在于题目有额外限制条件,程序只能使用 O(k) 的额外空间,因此无法通过累加的方式将每一行都输出打印。
|
|
|
|
|
|
|
|
|
|
|
|
这里依旧使用杨辉三角的规律,很隐藏的规律:对于杨辉三角的同一行,第 ( i + 1) 项是第 i 项的` ( k - i ) /( i + 1 )` 倍。
|
|
|
|
|
|
|
|
|
|
|
|
比如:
|
|
|
|
|
|
|
|
|
|
|
|
- 第 k 索引行的第 0 项:1
|
|
|
|
|
|
- 第 k 索引行的第 1 项:1 * k
|
|
|
|
|
|
- 第 k 索引行的第 2 项:1 * k * ( k - 1) / 2
|
|
|
|
|
|
- 第 k 索引行的第 3 项:[1 * k * ( k - 1) / 2 ] * ( k - 2 ) / 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
### 代码实现
|
|
|
|
|
|
|
|
|
|
|
|
```java
|
|
|
|
|
|
class Solution {
|
|
|
|
|
|
public List<Integer> getRow(int rowIndex) {
|
|
|
|
|
|
List<Integer> res = new ArrayList<>(rowIndex + 1);
|
|
|
|
|
|
long index = 1;
|
|
|
|
|
|
for (int i = 0; i <= rowIndex; i++) {
|
|
|
|
|
|
res.add((int) index);
|
|
|
|
|
|
index = index * ( rowIndex - i ) / ( i + 1 );
|
|
|
|
|
|
}
|
|
|
|
|
|
return res;
|
|
|
|
|
|
}
|
|
|
|
|
|
}
|
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
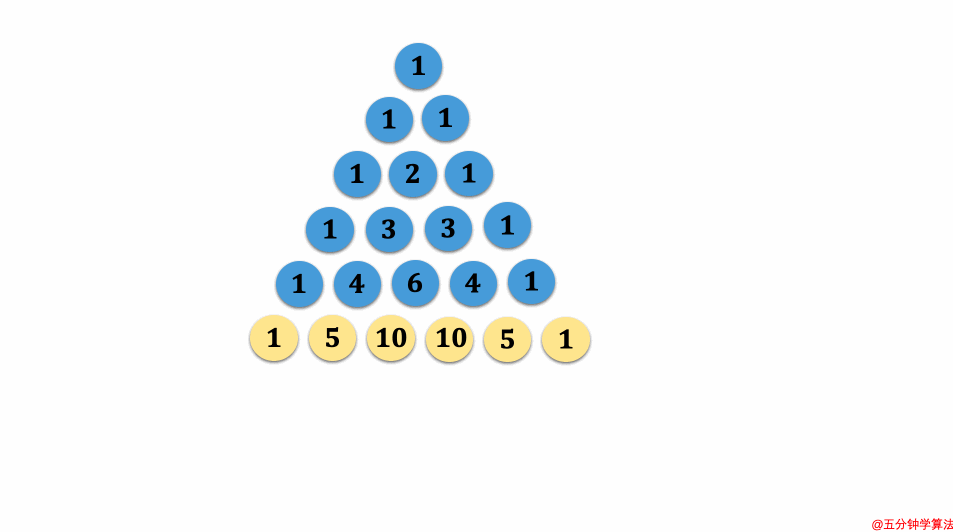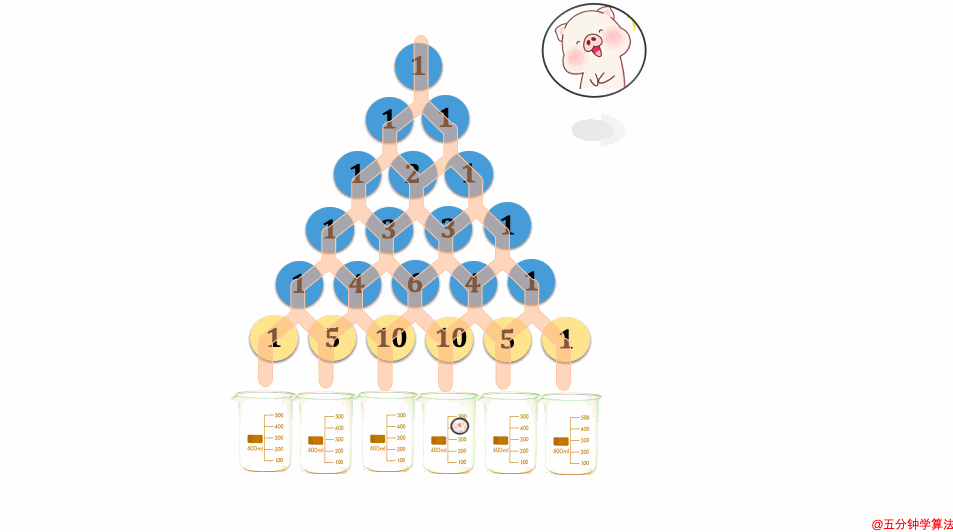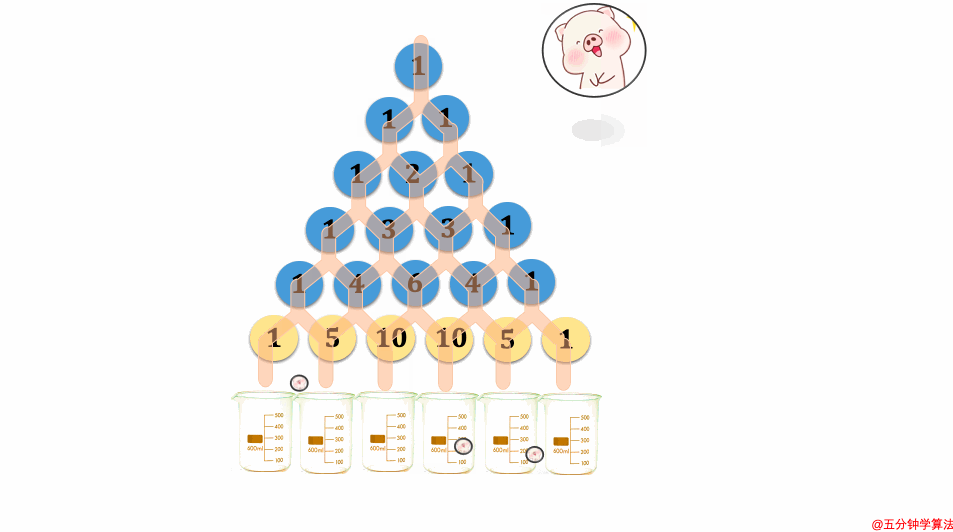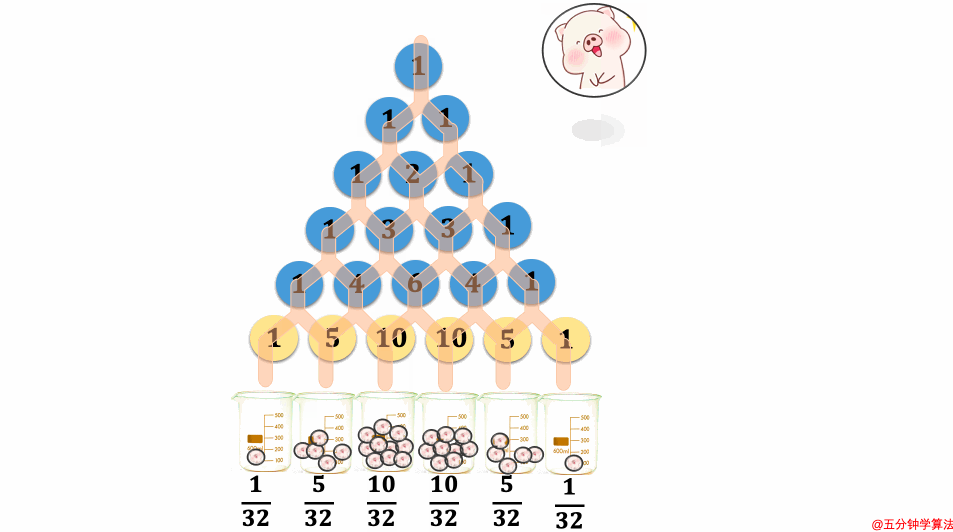
## 一个有趣的结论
|
|
|
|
|
|
|
|
|
|
|
|
感兴趣小伙伴的可以搜索一下李永乐讲得抽奖概率相关的视频,里面提及到了很多杨辉三角的神奇特点。
|
2019-11-14 11:00:28 +08:00
|
|
|
|
|
2019-05-09 16:57:58 +08:00
|
|
|
|
|
|
|
|
|
|
|
2019-11-14 11:00:28 +08:00
|
|
|
|

|