mirror of
https://gitee.com/TheAlgorithms/LeetCodeAnimation.git
synced 2024-12-06 15:19:44 +08:00
98 lines
3.0 KiB
Markdown
98 lines
3.0 KiB
Markdown
|
|
# LeetCode 第 209 号问题:长度最小的子数组
|
|||
|
|
|
|||
|
|
> 本文首发于公众号「五分钟学算法」,是[图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>)系列文章之一。
|
|||
|
|
>
|
|||
|
|
> 个人网站:[https://www.cxyxiaowu.com](https://www.cxyxiaowu.com)
|
|||
|
|
|
|||
|
|
题目来源于 LeetCode 上第 209 号问题:长度最小的子数组。题目难度为 Medium,目前通过率为 25.8% 。
|
|||
|
|
|
|||
|
|
### 题目描述
|
|||
|
|
|
|||
|
|
给定一个含有 **n** 个正整数的数组和一个正整数 **s ,**找出该数组中满足其和 **≥ s** 的长度最小的连续子数组**。**如果不存在符合条件的连续子数组,返回 0。
|
|||
|
|
|
|||
|
|
**示例:**
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
输入: s = 7, nums = [2,3,1,2,4,3]
|
|||
|
|
输出: 2
|
|||
|
|
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
**进阶:**
|
|||
|
|
|
|||
|
|
如果你已经完成了*O*(*n*) 时间复杂度的解法, 请尝试 *O*(*n* log *n*) 时间复杂度的解法。
|
|||
|
|
|
|||
|
|
### 题目解析
|
|||
|
|
|
|||
|
|
定义两个指针 left 和 right ,分别记录子数组的左右的边界位置。
|
|||
|
|
|
|||
|
|
|
|||
|
|
* (1)让 right 向右移,直到子数组和大于等于给定值或者 right 达到数组末尾;
|
|||
|
|
|
|||
|
|
* (2)更新最短距离,将 left 像右移一位,sum 减去移去的值;
|
|||
|
|
|
|||
|
|
* (3)重复(1)(2)步骤,直到 right 到达末尾,且 left 到达临界位置
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
### 动画描述
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
设置滑动窗口的长度为 0 ,位于数轴的最左端。
|
|||
|
|
|
|||
|
|
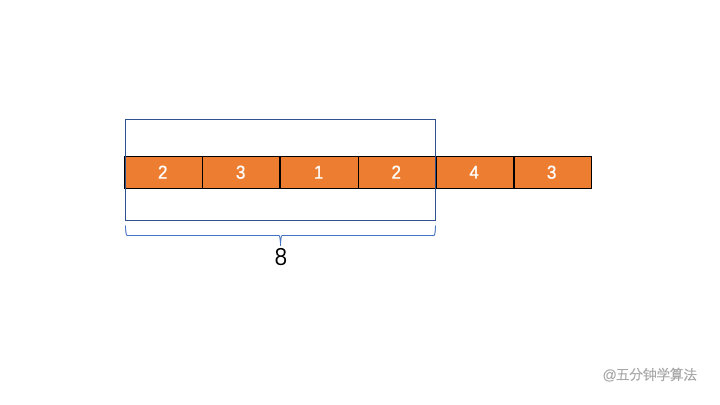
##### 1 .滑动窗口右端 R 开始移动,直到区间满足给定的条件,也就是和大于 7 ,此时停止于第三个元素 2,当前的最优长度为 4
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
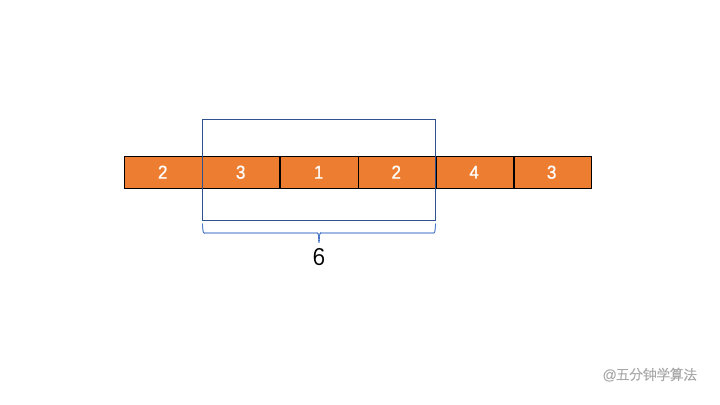
##### 2. 滑动窗口左端 L 开始移动,缩小滑动窗口的大小,停止于第一个元素 3,此时区间和为 6,使得区间和不满足给定的条件(此时不大于 7)
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
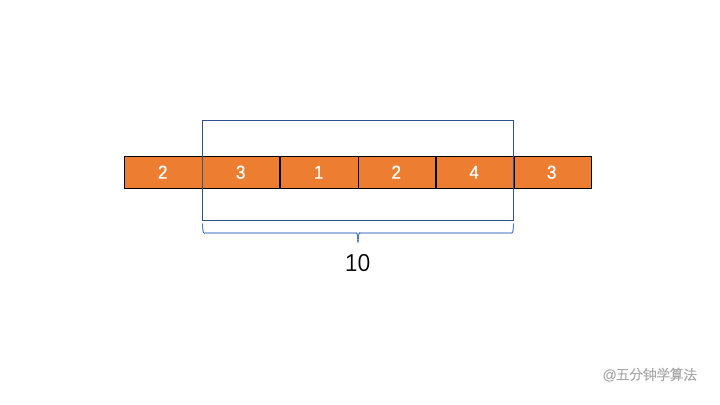
#### 3. 滑动窗口右端 R 继续移动,停止于第四个元素 4,此时和位 10 ,但最优长度仍然为 4
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
### 代码实现
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
// 滑动窗口的思路
|
|||
|
|
// 时间复杂度: O(n)
|
|||
|
|
// 空间复杂度: O(1)
|
|||
|
|
class Solution {
|
|||
|
|
public int minSubArrayLen(int s, int[] nums) {
|
|||
|
|
int l= 0,r = -1; // nums[l...r]为我们的滑动窗口
|
|||
|
|
int sum = 0;
|
|||
|
|
int result = nums.length + 1;
|
|||
|
|
while (l < nums.length){ // 窗口的左边界在数组范围内,则循环继续
|
|||
|
|
|
|||
|
|
if( r+1 <nums.length && sum < s){
|
|||
|
|
r++;
|
|||
|
|
sum += nums[r];
|
|||
|
|
}else { // r已经到头 或者 sum >= s
|
|||
|
|
sum -= nums[l];
|
|||
|
|
l++;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
if(sum >= s){
|
|||
|
|
result = (r-l+1) < result ? (r-l+1) : result ;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
if(result==nums.length+1){
|
|||
|
|
return 0;
|
|||
|
|
}
|
|||
|
|
return result;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|

|