Merge branch 'master' of github.com:wangzheng0822/algo

.gitignore

@@ -18,6 +18,7 @@
 *.zip
 *.tar.gz
 *.rar
+*.DS_Store
 
 # virtual machine crash logs, see http://www.java.com/en/download/help/error_hotspot.xml
 hs_err_pid*

c-cpp/18_hashtable/hash_map.cc

@@ -0,0 +1,98 @@
+/**
+ * Created by Liam Huang (Liam0205) on 2018/08/14.
+ * This is an old test file for hash_map, created by Liam.
+ * Just for showing the inner logic for hash_map class template.
+ * Original posted on:
+ *   https://github.com/Liam0205/leetcode/tree/master/met/hash_map.cc
+ */
+
+#include <iostream>
+#include <utility>
+#include <vector>
+#include <functional>
+#include <memory>
+
+template <typename Key, typename T, typename Hash = std::hash<Key>>
+class hash_map {
+  public:
+    using key_type = Key;
+    using mapped_type = T;
+    using value_type = std::pair<const key_type, mapped_type>;
+    using size_type = size_t;
+    using hasher = std::hash<Key>;
+
+  private:  // helper
+    using wrapper = std::shared_ptr<value_type>;
+
+  public:  // constructor
+    hash_map() {
+        container_.resize(primes_[size_level_]);
+    }
+
+  public:  // capacity
+    bool empty() const { return empty_; }
+    size_type size() const { return size_; }
+    size_type max_size() const { return primes_[size_level_]; }
+
+  public:  // find and modify
+    mapped_type& operator[](const key_type& key) {
+        auto hashed = find_hash(key);
+        if (not(container_[hashed]) and construct_new_on_position(hashed, key) and
+                load_factor() > max_load_factor()) {
+            expand();
+        }
+        return container_[hashed]->second;
+    }
+
+  public:  // hash policy
+    double load_factor() const { return static_cast<double>(size()) / max_size(); }
+    double max_load_factor() const { return max_load_factor_; }
+    void expand() const {
+        ++size_level_;
+        std::vector<wrapper> temp;
+        temp.resize(primes_[size_level_]);
+        for (auto w : container_) {
+            if (nullptr != w) {
+                auto hashed = find_hash(w->first);
+                temp[hashed] = w;
+            }
+        }
+        container_ = std::move(temp);
+    }
+
+  private:  // helper functions
+    size_type find_hash(const key_type& key) const {
+        const size_t csz = container_.size();
+        size_t count = 0;
+        size_t hashed = hasher_(key) % csz;
+        while (nullptr != container_[hashed] and container_[hashed]->first != key) {
+            hashed = (hashed + ++count) % csz;
+        }
+        return hashed;
+    }
+    bool construct_new_on_position(const size_type pos, const key_type& key) {
+        empty_ = false;
+        ++size_;
+        container_[pos] = std::make_shared<value_type>(std::make_pair(key, mapped_type()));
+        return true;
+    }
+
+  private:
+    const hasher hasher_ = hasher();
+    mutable size_t size_level_ = 0;
+    mutable std::vector<wrapper> container_;
+    static const size_t primes_[];
+    bool empty_ = true;
+    size_type size_ = 0;
+    double max_load_factor_ = 0.75;
+};
+template <typename Key, typename T, typename Hash>
+const size_t hash_map<Key, T, Hash>::primes_[] = {7, 17, 29, 53, 101, 211, 401, 809, 1601, 3203};  // ...
+
+int main() {
+    hash_map<int, int> test;
+    test[1];
+    test[2] = 2;
+    std::cout << test[1] << ' ' << test[2] << std::endl;
+    return 0;
+}

java/06_linkedlist/LRUBaseLinkedList.java

@@ -0,0 +1,176 @@
+package linked.singlelist;
+
+
+import java.util.Scanner;
+
+/**
+ * 基于单链表LRU算法（java）
+ *
+ * @author hoda
+ * @create 2018-12-17
+ */
+public class LRUBaseLinkedList<T> {
+
+    /**
+     * 默认链表容量
+     */
+    private final static Integer DEFAULT_CAPACITY = 10;
+
+    /**
+     * 头结点
+     */
+    private SNode<T> headNode;
+
+    /**
+     * 链表长度
+     */
+    private Integer length;
+
+    /**
+     * 链表容量
+     */
+    private Integer capacity;
+
+    public LRUBaseLinkedList() {
+        this.headNode = new SNode<>();
+        this.capacity = DEFAULT_CAPACITY;
+        this.length = 0;
+    }
+
+    public LRUBaseLinkedList(Integer capacity) {
+        this.headNode = new SNode<>();
+        this.capacity = capacity;
+        this.length = 0;
+    }
+
+    public void add(T data) {
+        SNode preNode = findPreNode(data);
+
+        // 链表中存在，删除原数据，再插入到链表的头部
+        if (preNode != null) {
+            deleteElemOptim(preNode);
+            intsertElemAtBegin(data);
+        } else {
+            if (length >= this.capacity) {
+                //删除尾结点
+                deleteElemAtEnd();
+            }
+            intsertElemAtBegin(data);
+        }
+    }
+
+    /**
+     * 删除preNode结点下一个元素
+     *
+     * @param preNode
+     */
+    private void deleteElemOptim(SNode preNode) {
+        SNode temp = preNode.getNext();
+        preNode.setNext(temp.getNext());
+        temp = null;
+        length--;
+    }
+
+    /**
+     * 链表头部插入节点
+     *
+     * @param data
+     */
+    private void intsertElemAtBegin(T data) {
+        SNode next = headNode.getNext();
+        headNode.setNext(new SNode(data, next));
+        length++;
+    }
+
+    /**
+     * 获取查找到元素的前一个结点
+     *
+     * @param data
+     * @return
+     */
+    private SNode findPreNode(T data) {
+        SNode node = headNode;
+        while (node.getNext() != null) {
+            if (data.equals(node.getNext().getElement())) {
+                return node;
+            }
+            node = node.getNext();
+        }
+        return null;
+    }
+
+    /**
+     * 删除尾结点
+     */
+    private void deleteElemAtEnd() {
+        SNode ptr = headNode;
+        // 空链表直接返回
+        if (ptr.getNext() == null) {
+            return;
+        }
+
+        // 倒数第二个结点
+        while (ptr.getNext().getNext() != null) {
+            ptr = ptr.getNext();
+        }
+
+        SNode tmp = ptr.getNext();
+        ptr.setNext(null);
+        tmp = null;
+        length--;
+    }
+
+    private void printAll() {
+        SNode node = headNode.getNext();
+        while (node != null) {
+            System.out.print(node.getElement() + ",");
+            node = node.getNext();
+        }
+        System.out.println();
+    }
+
+    public class SNode<T> {
+
+        private T element;
+
+        private SNode next;
+
+        public SNode(T element) {
+            this.element = element;
+        }
+
+        public SNode(T element, SNode next) {
+            this.element = element;
+            this.next = next;
+        }
+
+        public SNode() {
+            this.next = null;
+        }
+
+        public T getElement() {
+            return element;
+        }
+
+        public void setElement(T element) {
+            this.element = element;
+        }
+
+        public SNode getNext() {
+            return next;
+        }
+
+        public void setNext(SNode next) {
+            this.next = next;
+        }
+    }
+
+    public static void main(String[] args) {
+        LRUBaseLinkedList list = new LRUBaseLinkedList();
+        Scanner sc = new Scanner(System.in);
+        while (true) {
+            list.add(sc.nextInt());
+            list.printAll();
+        }
+    }
+}

notes/18_hashtable/readme.md

@@ -1,69 +1,69 @@
-# 散列表
-
-散列表是数组的一种扩展，利用数组下标的随机访问特性。
-
-## 散列思想
-
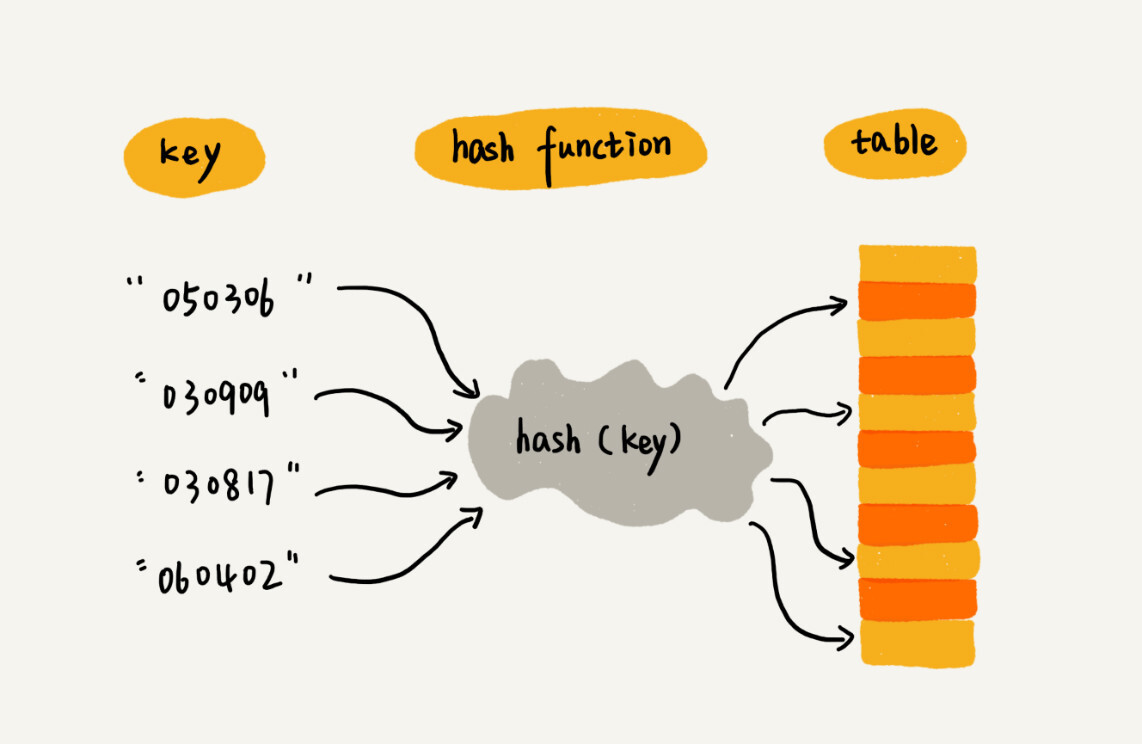
-* 键/关键字/Key：用来标识一个数据
-* 散列函数/哈希函数/Hash：将 Key 映射到数组下标的函数
-* 散列值/哈希值：Key 经过散列函数得到的数值
-
-![](https://static001.geekbang.org/resource/image/92/73/92c89a57e21f49d2f14f4424343a2773.jpg)
-
-本质：利用散列函数将关键字映射到数组下标，而后利用数组随机访问时间复杂度为 $\Theta(1)$ 的特性快速访问。
-
-## 散列函数
-
-* 形式：`hash(key)`
-* 基本要求
-  1. 散列值是非负整数
-  1. 如果 `key1 == key2`，那么 `hash(key1) == hash(key2)`
-  1. 如果 `key1 != key2`，那么 `hash(key1) != hash(key2)`
-
-第 3 个要求，实际上不可能对任意的 `key1` 和 `key2` 都成立。因为通常散列函数的输出范围有限而输入范围无限。
-
-## 散列冲突¡
-
-* 散列冲突：`key1 != key2` 但 `hash(key1) == hash(key2)`
-
-散列冲突会导致不同键值映射到散列表的同一个位置。为此，我们需要解决散列冲突带来的问题。
-
-### 开放寻址法
-
-如果遇到冲突，那就继续寻找下一个空闲的槽位。
-
-#### 线性探测
-
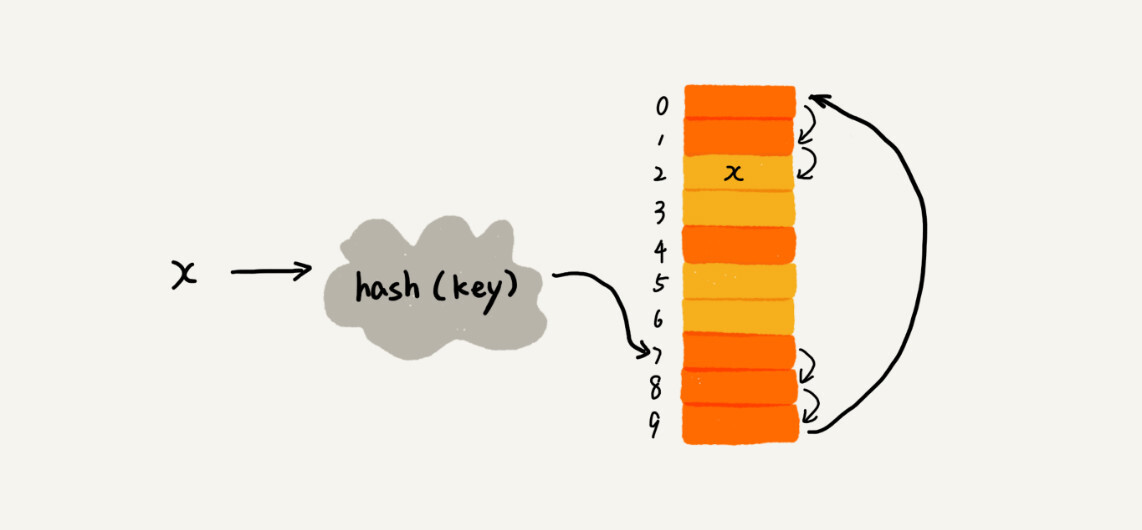
-插入时，如果遇到冲突，那就依次往下寻找下一个空闲的槽位。（橙色表示已被占用的槽位，黄色表示空闲槽位）
-
-![](https://static001.geekbang.org/resource/image/5c/d5/5c31a3127cbc00f0c63409bbe1fbd0d5.jpg)
-
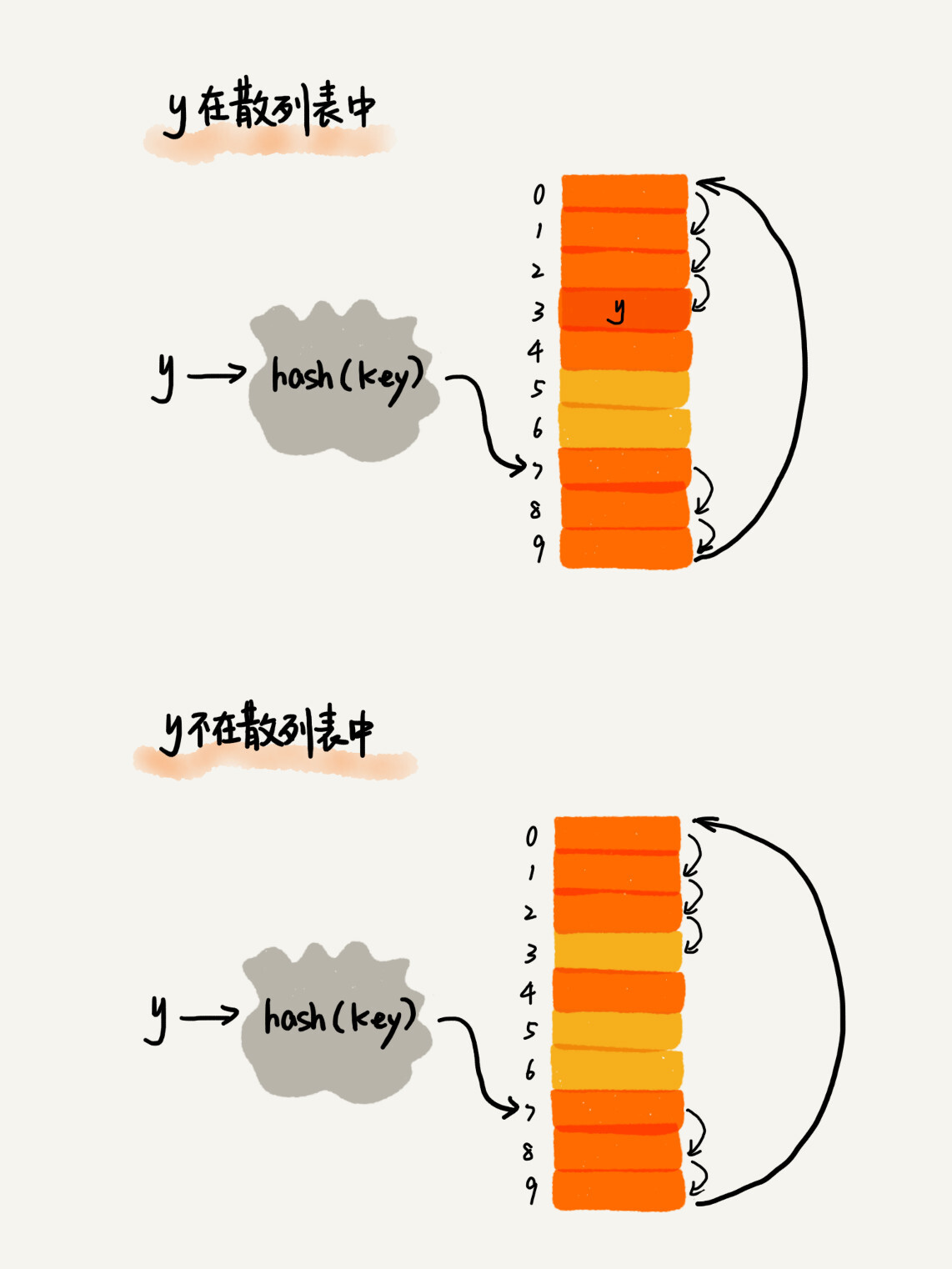
-查找时，如果目标槽位上不是目标数据，则依次往下寻找；直至遇见目标数据或空槽位。
-
-![](https://static001.geekbang.org/resource/image/91/ff/9126b0d33476777e7371b96e676e90ff.jpg)
-
-删除时，标记为 `deleted`，而不是直接删除。
-
-#### 平方探测（Quadratic probing）
-
-插入时，如果遇到冲突，那就往后寻找下一个空闲的槽位，其步长为 $1^2$, $2^2$, $3^2$, $\ldots$。
-
-查找时，如果目标槽位上不是目标数据，则依次往下寻找，其步长为 $1^2$, $2^2$, $3^2$, $\ldots$；直至遇见目标数据或空槽位。
-
-删除时，标记为 `deleted`，而不是直接删除。
-
-#### 装载因子（load factor）
-
-$\text{load factor} = \frac{size()}{capacity()}$
-
-### 链表法
-
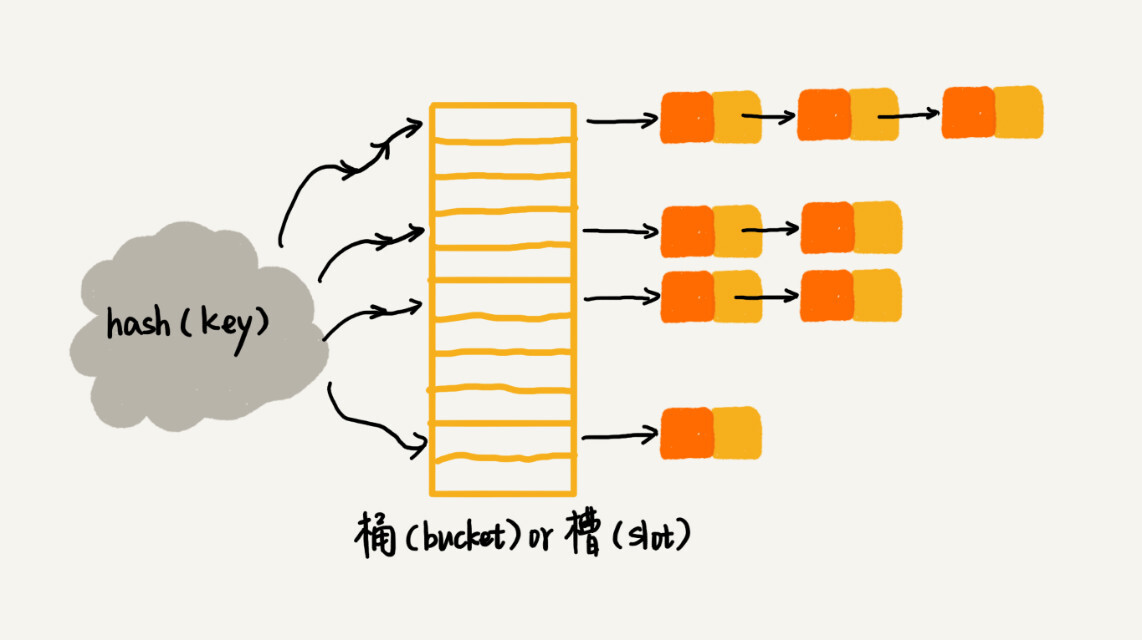
-所有散列值相同的 key 以链表的形式存储在同一个槽位中。
-
-![](https://static001.geekbang.org/resource/image/a4/7f/a4b77d593e4cb76acb2b0689294ec17f.jpg)
-
-插入时，不论是否有冲突，直接插入目标位置的链表。
-
-查找时，遍历目标位置的链表来查询。
-
-删除时，遍历目标位置的链表来删除。
+# 散列表
+
+散列表是数组的一种扩展，利用数组下标的随机访问特性。
+
+## 散列思想
+
+* 键/关键字/Key：用来标识一个数据
+* 散列函数/哈希函数/Hash：将 Key 映射到数组下标的函数
+* 散列值/哈希值：Key 经过散列函数得到的数值
+
+![](https://static001.geekbang.org/resource/image/92/73/92c89a57e21f49d2f14f4424343a2773.jpg)
+
+本质：利用散列函数将关键字映射到数组下标，而后利用数组随机访问时间复杂度为 $\Theta(1)$ 的特性快速访问。
+
+## 散列函数
+
+* 形式：`hash(key)`
+* 基本要求
+  1. 散列值是非负整数
+  1. 如果 `key1 == key2`，那么 `hash(key1) == hash(key2)`
+  1. 如果 `key1 != key2`，那么 `hash(key1) != hash(key2)`
+
+第 3 个要求，实际上不可能对任意的 `key1` 和 `key2` 都成立。因为通常散列函数的输出范围有限而输入范围无限。
+
+## 散列冲突
+
+* 散列冲突：`key1 != key2` 但 `hash(key1) == hash(key2)`
+
+散列冲突会导致不同键值映射到散列表的同一个位置。为此，我们需要解决散列冲突带来的问题。
+
+### 开放寻址法
+
+如果遇到冲突，那就继续寻找下一个空闲的槽位。
+
+#### 线性探测
+
+插入时，如果遇到冲突，那就依次往下寻找下一个空闲的槽位。（橙色表示已被占用的槽位，黄色表示空闲槽位）
+
+![](https://static001.geekbang.org/resource/image/5c/d5/5c31a3127cbc00f0c63409bbe1fbd0d5.jpg)
+
+查找时，如果目标槽位上不是目标数据，则依次往下寻找；直至遇见目标数据或空槽位。
+
+![](https://static001.geekbang.org/resource/image/91/ff/9126b0d33476777e7371b96e676e90ff.jpg)
+
+删除时，标记为 `deleted`，而不是直接删除。
+
+#### 平方探测（Quadratic probing）
+
+插入时，如果遇到冲突，那就往后寻找下一个空闲的槽位，其步长为 $1^2$, $2^2$, $3^2$, $\ldots$。
+
+查找时，如果目标槽位上不是目标数据，则依次往下寻找，其步长为 $1^2$, $2^2$, $3^2$, $\ldots$；直至遇见目标数据或空槽位。
+
+删除时，标记为 `deleted`，而不是直接删除。
+
+#### 装载因子（load factor）
+
+$\text{load factor} = \frac{size()}{capacity()}$
+
+### 链表法
+
+所有散列值相同的 key 以链表的形式存储在同一个槽位中。
+
+![](https://static001.geekbang.org/resource/image/a4/7f/a4b77d593e4cb76acb2b0689294ec17f.jpg)
+
+插入时，不论是否有冲突，直接插入目标位置的链表。
+
+查找时，遍历目标位置的链表来查询。
+
+删除时，遍历目标位置的链表来删除。

notes/19_hashtable/readme.md

@@ -1,59 +1,59 @@
-# 散列表
-
-核心：散列表的效率并不总是 $O(1)$，仅仅是在理论上能达到 $O(1)$。实际情况中，恶意攻击者可以通过精心构造数据，使得散列表的性能急剧下降。
-
-如何设计一个工业级的散列表？
-
-## 散列函数
-
-* 不能过于复杂——避免散列过程耗时
-* 散列函数的结果要尽可能均匀——最小化散列冲突
-
-## 装载因子过大怎么办
-
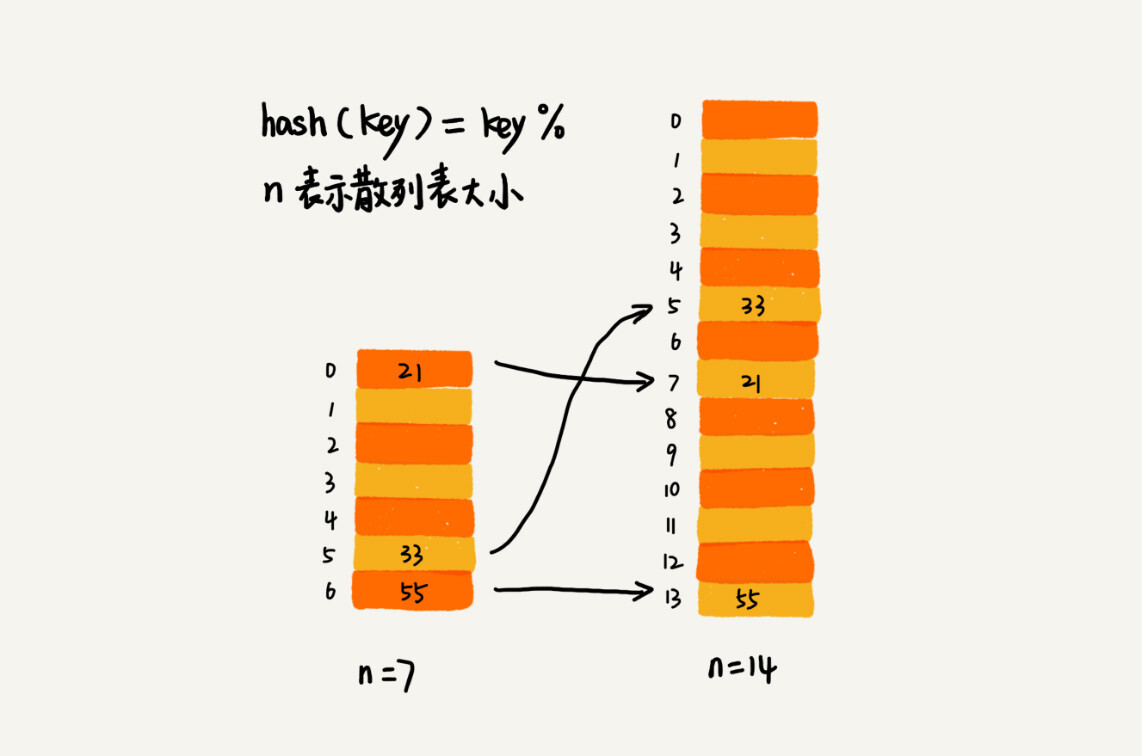
-动态扩容。涉及到 rehash，效率可能很低。
-
-![](https://static001.geekbang.org/resource/image/67/43/67d12e07a7d673a9c1d14354ad029443.jpg)
-
-如何避免低效扩容？
-
-——将 rehash 的步骤，均摊到每一次插入中去：
-
-* 申请新的空间
-* 不立即使用
-* 每次来了新的数据，往新表插入数据
-* 同时，取出旧表的一个数据，插入新表
-
-![](https://static001.geekbang.org/resource/image/6d/cb/6d6736f986ec4b75dabc5472965fb9cb.jpg)
-
-## 解决冲突
-
-开放寻址法，优点：
-
-* 不需要额外空间
-* 有效利用 CPU 缓存
-* 方便序列化
-
-开放寻址法，缺点：
-
-* 查找、删除数据时，涉及到 `delete` 标志，相对麻烦
-* 冲突的代价更高
-* 对装载因子敏感
-
-链表法，优点：
-
-* 内存利用率较高——链表的优点
-* 对装载因子不敏感
-
-链表法，缺点：
-
-* 需要额外的空间（保存指针）
-* 对 CPU 缓存不友好
-
-——将链表改造成更高效的数据结构，例如跳表、红黑树
-
-## 举个栗子（JAVA 中的 HashMap）
-
-* 初始大小：16
-* 装载因子：超过 0.75 时动态扩容
-* 散列冲突：优化版的链表法（当槽位冲突元素超过 8 时使用红黑树，否则使用链表）
+# 散列表
+
+核心：散列表的效率并不总是 $O(1)$，仅仅是在理论上能达到 $O(1)$。实际情况中，恶意攻击者可以通过精心构造数据，使得散列表的性能急剧下降。
+
+如何设计一个工业级的散列表？
+
+## 散列函数
+
+* 不能过于复杂——避免散列过程耗时
+* 散列函数的结果要尽可能均匀——最小化散列冲突
+
+## 装载因子过大怎么办
+
+动态扩容。涉及到 rehash，效率可能很低。
+
+![](https://static001.geekbang.org/resource/image/67/43/67d12e07a7d673a9c1d14354ad029443.jpg)
+
+如何避免低效扩容？
+
+——将 rehash 的步骤，均摊到每一次插入中去：
+
+* 申请新的空间
+* 不立即使用
+* 每次来了新的数据，往新表插入数据
+* 同时，取出旧表的一个数据，插入新表
+
+![](https://static001.geekbang.org/resource/image/6d/cb/6d6736f986ec4b75dabc5472965fb9cb.jpg)
+
+## 解决冲突
+
+开放寻址法，优点：
+
+* 不需要额外空间
+* 有效利用 CPU 缓存
+* 方便序列化
+
+开放寻址法，缺点：
+
+* 查找、删除数据时，涉及到 `delete` 标志，相对麻烦
+* 冲突的代价更高
+* 对装载因子敏感
+
+链表法，优点：
+
+* 内存利用率较高——链表的优点
+* 对装载因子不敏感
+
+链表法，缺点：
+
+* 需要额外的空间（保存指针）
+* 对 CPU 缓存不友好
+
+——将链表改造成更高效的数据结构，例如跳表、红黑树
+
+## 举个栗子（JAVA 中的 HashMap）
+
+* 初始大小：16
+* 装载因子：超过 0.75 时动态扩容
+* 散列冲突：优化版的链表法（当槽位冲突元素超过 8 时使用红黑树，否则使用链表）

notes/20_hashtable/readme.md

@@ -0,0 +1,35 @@
+# 散列表
+
+散列表和链表的组合？为什么呢？
+
+* 链表：涉及查找的操作慢，不连续存储；
+* 顺序表：支持随机访问，连续存储。
+
+散列表 + 链表：结合优点、规避缺点。
+
+## 结合散列表的 LRU 缓存淘汰算法
+
+缓存的操作接口：
+
+* 向缓存添加数据
+* 从缓存删除数据
+* 在缓存中查找数据
+
+然而——不管是添加还是删除，都涉及到查找数据。因此，单纯的链表效率低下。
+
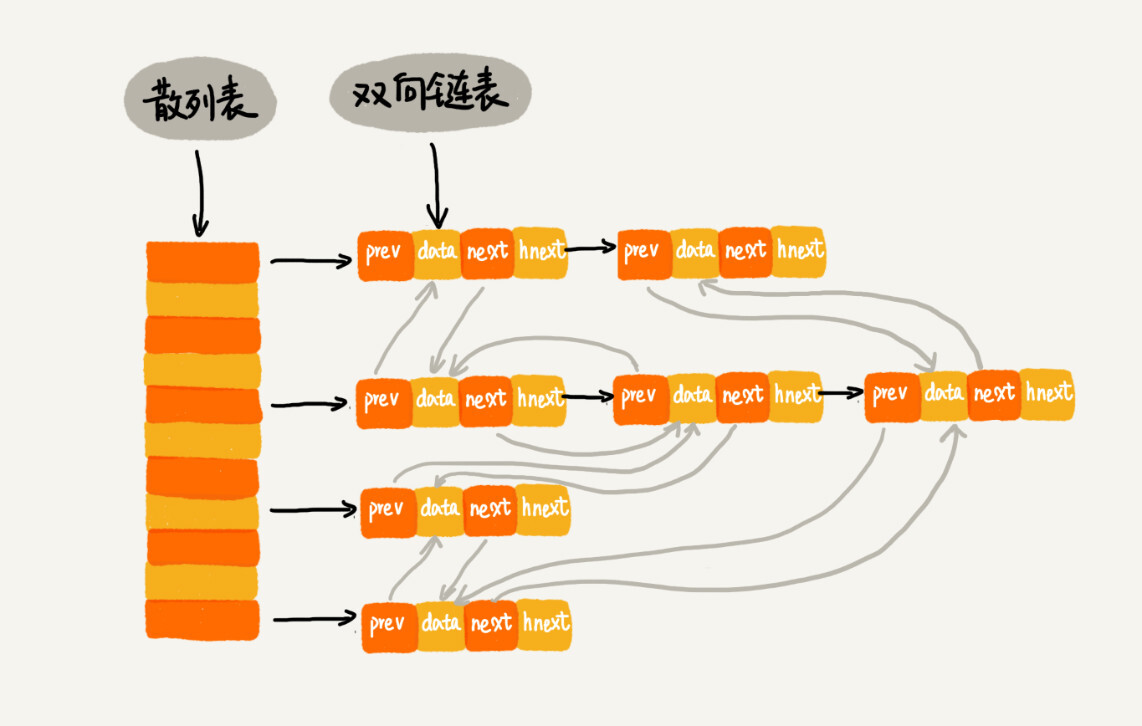
+魔改一把！
+
+![](https://static001.geekbang.org/resource/image/ea/6e/eaefd5f4028cc7d4cfbb56b24ce8ae6e.jpg)
+
+* `prev` 和 `next`：双向链表——LRU 的链表
+* `hnext`：单向链表——解决散列冲突的链表
+
+操作：
+
+* 在缓存中查找数据：利用散列表
+* 从缓存中删除数据：先利用散列表寻找数据，然后删除——改链表就好了，效率很高
+* 向缓存中添加数据：先利用散列表寻找数据，如果找到了，LRU 更新；如果没找到，直接添加在 LRU 链表尾部
+
+## Java: LinkedHashMap
+
+遍历时，按照访问顺序遍历。实现结构，与上述 LRU 的结构完全相同——只不过它不是缓存，不限制容量大小。

object-c/11_Sort/Sort.h

@@ -0,0 +1,24 @@
+//
+//  Sort.h
+//  test1231231
+//
+//  Created by Scarlett Che on 2018/12/12.
+//  Copyright © 2018 Scarlett Che. All rights reserved.
+//
+
+#import <Foundation/Foundation.h>
+
+NS_ASSUME_NONNULL_BEGIN
+
+@interface Sort : NSObject
+//  冒泡排序
++ (NSArray *)bubbleSortWithArray:(NSArray *)array;
+
+//  插入排序
++ (NSArray *)insertionSortWithArray:(NSArray *)array;
+
+//  选择排序
++ (NSArray *)selectionSortWithArray:(NSArray *)array;
+@end
+
+NS_ASSUME_NONNULL_END

object-c/11_Sort/Sort.m

@@ -0,0 +1,86 @@
+//
+//  Sort.m
+//  test1231231
+//
+//  Created by Scarlett Che on 2018/12/12.
+//  Copyright © 2018 Scarlett Che. All rights reserved.
+//
+
+#import "Sort.h"
+
+@implementation Sort
+//  冒泡排序
++ (NSArray *)bubbleSortWithArray:(NSArray *)array {
+    if (array.count <= 1) {
+        return array;
+    }
+    
+    NSMutableArray *aryM = array.mutableCopy;
+    
+    for (int i = 0; i < aryM.count - 1; i++) {
+        BOOL flag = NO; //  提前结束标记
+        for (int j = 0; j < aryM.count - i - 1; j++) {
+            NSInteger value1 = [aryM[j] integerValue];
+            NSInteger value2 = [aryM[j + 1] integerValue];
+            
+            if (value1 > value2) {
+                flag = YES;
+                [aryM exchangeObjectAtIndex:j withObjectAtIndex:j+1];
+            }
+        }
+        
+        
+        if (flag == NO) {
+            //  提前结束
+            break;
+        }
+    }
+    return aryM.copy;
+}
+
+//  插入排序
++ (NSArray *)insertionSortWithArray:(NSArray *)array {
+    NSMutableArray *aryU = array.mutableCopy;
+    
+    for (int i = 1; i < aryU.count; i++) {
+        NSInteger value = [aryU[i] integerValue];
+        
+        for (int j = 0; j < i; j ++) {
+            NSInteger sortedValue = [aryU[j] integerValue];
+            if (value < sortedValue) {
+                id obj = aryU[i];
+                [aryU removeObjectAtIndex:i];
+                [aryU insertObject:obj atIndex:j];
+                break;
+            }
+        }
+    }
+    return aryU.copy;
+}
+
+//  选择排序
++ (NSArray *)selectionSortWithArray:(NSArray *)array {
+    if (array.count <= 1) {
+        return array;
+    }
+    
+    NSMutableArray *aryM = array.mutableCopy;
+    for (int i = 0; i < array.count - 1; i++) {
+        NSInteger minIndex = NSNotFound;
+        NSInteger minValue = NSNotFound;
+        for (int j = i + 1; j < array.count - 1; j++) {
+            NSInteger tmp = [array[j] integerValue];
+            if (tmp < minValue) {
+                minValue = tmp;
+                minIndex = j;
+            }
+        }
+        
+        if (minIndex != NSNotFound && minValue != NSNotFound && minValue < [array[i] integerValue]) {
+            [aryM exchangeObjectAtIndex:minIndex withObjectAtIndex:i];
+        }
+        
+    }
+    return array;
+}
+@end

python/12_sorts/merge_sort.py

@@ -4,21 +4,23 @@
 
 from typing import List
 
+
 def merge_sort(a: List[int]):
-    _merge_sort_between(a, 0, len(a)-1)
+    _merge_sort_between(a, 0, len(a) - 1)
+
 
 def _merge_sort_between(a: List[int], low: int, high: int):
     # The indices are inclusive for both low and high.
-    if low >= high: return
-    mid = low + (high - low)//2
-    _merge_sort_between(a, low, mid)
-    _merge_sort_between(a, mid+1, high)
+    if low < high:
+        mid = low + (high - low) // 2
+        _merge_sort_between(a, low, mid)
+        _merge_sort_between(a, mid + 1, high)
+        _merge(a, low, mid, high)
 
-    _merge(a, low, mid, high)
 
 def _merge(a: List[int], low: int, mid: int, high: int):
     # a[low:mid], a[mid+1, high] are sorted.
-    i, j = low, mid+1
+    i, j = low, mid + 1
     tmp = []
     while i <= mid and j <= high:
         if a[i] <= a[j]:
@@ -29,8 +31,23 @@ def _merge(a: List[int], low: int, mid: int, high: int):
             j += 1
     start = i if i <= mid else j
     end = mid if i <= mid else high
-    tmp.extend(a[start:end+1])
-    a[low:high+1] = tmp
+    tmp.extend(a[start:end + 1])
+    a[low:high + 1] = tmp
+
+
+def test_merge_sort():
+    a1 = [3, 5, 6, 7, 8]
+    merge_sort(a1)
+    assert a1 == [3, 5, 6, 7, 8]
+    a2 = [2, 2, 2, 2]
+    merge_sort(a2)
+    assert a2 == [2, 2, 2, 2]
+    a3 = [4, 3, 2, 1]
+    merge_sort(a3)
+    assert a3 == [1, 2, 3, 4]
+    a4 = [5, -1, 9, 3, 7, 8, 3, -2, 9]
+    merge_sort(a4)
+    assert a4 == [-2, -1, 3, 3, 5, 7, 8, 9, 9]
 
 
 if __name__ == "__main__":
@@ -45,4 +62,4 @@ if __name__ == "__main__":
     merge_sort(a3)
     print(a3)
     merge_sort(a4)
-    print(a4)
+    print(a4)

python/12_sorts/quick_sort.py

@@ -5,22 +5,25 @@
 from typing import List
 import random
 
+
 def quick_sort(a: List[int]):
-    _quick_sort_between(a, 0, len(a)-1)
+    _quick_sort_between(a, 0, len(a) - 1)
+
 
 def _quick_sort_between(a: List[int], low: int, high: int):
-    if low >= high: return
-    # get a random position as the pivot
-    k = random.randint(low, high)
-    a[low], a[k] = a[k], a[low]
+    if low < high:
+        # get a random position as the pivot
+        k = random.randint(low, high)
+        a[low], a[k] = a[k], a[low]
+
+        m = _partition(a, low, high)  # a[m] is in final position
+        _quick_sort_between(a, low, m - 1)
+        _quick_sort_between(a, m + 1, high)
 
-    m = _partition(a, low, high)   # a[m] is in final position
-    _quick_sort_between(a, low, m-1)
-    _quick_sort_between(a, m+1, high)
 
 def _partition(a: List[int], low: int, high: int):
     pivot, j = a[low], low
-    for i in range(low+1, high+1):
+    for i in range(low + 1, high + 1):
         if a[i] <= pivot:
             j += 1
             a[j], a[i] = a[i], a[j]  # swap
@@ -28,6 +31,21 @@ def _partition(a: List[int], low: int, high: int):
     return j
 
 
+def test_quick_sort():
+    a1 = [3, 5, 6, 7, 8]
+    quick_sort(a1)
+    assert a1 == [3, 5, 6, 7, 8]
+    a2 = [2, 2, 2, 2]
+    quick_sort(a2)
+    assert a2 == [2, 2, 2, 2]
+    a3 = [4, 3, 2, 1]
+    quick_sort(a3)
+    assert a3 == [1, 2, 3, 4]
+    a4 = [5, -1, 9, 3, 7, 8, 3, -2, 9]
+    quick_sort(a4)
+    assert a4 == [-2, -1, 3, 3, 5, 7, 8, 9, 9]
+
+
 if __name__ == "__main__":
     a1 = [3, 5, 6, 7, 8]
     a2 = [2, 2, 2, 2]
@@ -40,4 +58,4 @@ if __name__ == "__main__":
     quick_sort(a3)
     print(a3)
     quick_sort(a4)
-    print(a4)
+    print(a4)

python/14_sorts/counting_sort.py

@@ -23,7 +23,7 @@ def counting_sort(a: List[int]):
         a_sorted[index] = num
         counts[num] -= 1
     
-    a = a_sorted
+    a[:] = a_sorted
 
 
 if __name__ == "__main__":
@@ -37,4 +37,4 @@ if __name__ == "__main__":
 
     a3 = [4, 5, 0, 9, 3, 3, 1, 9, 8, 7]
     counting_sort(a3)
-    print(a3)
+    print(a3)

python/35_trie/trie_.py

@@ -15,16 +15,18 @@ class Node:
         self.children = []
 
     def insert_child(self, c):
+        self._insert_child(Node(c))
+
+    def _insert_child(self, node):
         """
         插入一个子节点
         :param c:
         :return:
         """
-        v = ord(c)
+        v = ord(node.data)
         idx = self._find_insert_idx(v)
         length = len(self.children)
 
-        node = Node(c)
         if idx == length:
             self.children.append(node)
         else:
@@ -33,6 +35,9 @@ class Node:
                 self.children[i] = self.children[i-1]
             self.children[idx] = node
 
+    def has_child(self, c):
+        return True if self.get_child(c) is not None else False
+
     def get_child(self, c):
         """
         搜索子节点并返回

python/36_ac_automata/ac_automata.py

@@ -0,0 +1,80 @@
+"""
+    Aho-Corasick Algorithm
+
+    Author: Wenru Dong
+"""
+
+from collections import deque
+from typing import List
+
+class ACNode:
+    def __init__(self, data: str):
+        self._data = data
+        self._children = [None] * 26
+        self._is_ending_char = False
+        self._length = -1
+        self._suffix = None
+    
+
+class ACAutomata:
+    def __init__(self):
+        self._root = ACNode("/")
+
+    def _build_suffix_link(self) -> None:
+        q = deque()
+        q.append(self._root)
+        while q:
+            node = q.popleft()
+            for child in node._children:
+                if child:
+                    if node == self._root:
+                        child._suffix = self._root
+                    else:
+                        suffix = node._suffix
+                        while suffix:
+                            suffix_child = suffix._children[ord(child._data) - ord("a")]
+                            if suffix_child:
+                                child._suffix = suffix_child
+                                break
+                            suffix = suffix._suffix
+                        if not suffix:
+                            child._suffix = self._root
+                    q.append(child)
+
+    def _insert(self, text: str) -> None:
+        node = self._root
+        for index, char in map(lambda x: (ord(x) - ord("a"), x), text):
+            if not node._children[index]:
+                node._children[index] = ACNode(char)
+            node = node._children[index]
+        node._is_ending_char = True
+        node._length = len(text)
+
+    def insert(self, patterns: List[str]) -> None:
+        for pattern in patterns:
+            self._insert(pattern)
+        self._build_suffix_link()
+
+    def match(self, text: str) -> None:
+        node = self._root
+        for i, char in enumerate(text):
+            index = ord(char) - ord("a")
+            while not node._children[index] and node != self._root:
+                node = node._suffix
+            node = node._children[index]
+            if not node:
+                node = self._root
+            tmp = node
+            while tmp != self._root:
+                if tmp._is_ending_char:
+                    print(f"匹配起始下标{i - tmp._length + 1}，长度{tmp._length}")
+                tmp = tmp._suffix
+
+
+if __name__ == "__main__":
+
+    patterns = ["at", "art", "oars", "soar"]
+    ac = ACAutomata()
+    ac.insert(patterns)
+    
+    ac.match("soarsoars")

python/36_ac_automata/ac_automata_.py

@@ -0,0 +1,88 @@
+#!/usr/bin/python
+# -*- coding: UTF-8 -*-
+
+from trie_ import Node, Trie
+from queue import Queue
+
+
+class ACNode(Node):
+    def __init__(self, c: str):
+        super(ACNode, self).__init__(c)
+        self.fail = None
+        self.length = 0
+
+    def insert_child(self, c: str):
+        self._insert_child(ACNode(c))
+
+
+class ACTrie(Trie):
+    def __init__(self):
+        self.root = ACNode(None)
+
+
+def ac_automata(main: str, ac_trie: ACTrie) -> list:
+    root = ac_trie.root
+    build_failure_pointer(ac_trie)
+
+    ret = []
+    p = root
+    for i, c in enumerate(main):
+        while p != root and not p.has_child(c):
+            p = p.fail
+
+        if p.has_child(c):  # a char matched, try to find all potential pattern matched
+            q = p.get_child(c)
+            while q != root:
+                if q.is_ending_char:
+                    ret.append((i-q.length+1, i))
+                    # ret.append(main[i-q.length+1:i+1])
+                q = q.fail
+            p = p.get_child(c)
+
+    return ret
+
+
+def build_failure_pointer(ac_trie: ACTrie) -> None:
+    root = ac_trie.root
+
+    # queue: [(node, node.length) ....]
+    node_queue = Queue()
+    node_queue.put((root, root.length))
+
+    root.fail = None
+    while not node_queue.empty():
+        p, length = node_queue.get()
+        for pc in p.children:
+            pc.length = length + 1
+            if p == root:
+                pc.fail = root
+            else:
+                q = p.fail
+                # same as kmp
+                while q != root and not q.has_child(pc.data):
+                    q = q.fail
+
+                # cases now:
+                # 1. q == root
+                # 2. q != root and q.has_child(pc.data)
+                if q.has_child(pc.data):
+                    pc.fail = q.get_child(pc.data)
+                else:
+                    pc.fail = root
+            node_queue.put((pc, pc.length))
+
+
+if __name__ == '__main__':
+    ac_trie = ACTrie()
+    ac_trie.gen_tree(['fuck', 'shit', 'TMD', '傻叉'])
+
+    print('--- ac automata ---')
+    m_str = 'fuck you, what is that shit, TMD你就是个傻叉傻叉傻叉叉'
+    print('original str  : {}'.format(m_str))
+
+    filter_range_list = ac_automata(m_str, ac_trie)
+    str_filtered = m_str
+    for start, end in filter_range_list:
+        str_filtered = str_filtered.replace(str_filtered[start:end+1], '*'*(end+1-start))
+
+    print('after filtered: {}'.format(str_filtered))

python/38_divide_and_conquer/merge_sort_counting.py

@@ -0,0 +1,51 @@
+#!/usr/bin/python
+# -*- coding: UTF-8 -*-
+
+inversion_num = 0
+
+
+def merge_sort_counting(nums, start, end):
+    if start >= end:
+        return
+
+    mid = (start + end)//2
+    merge_sort_counting(nums, start, mid)
+    merge_sort_counting(nums, mid+1, end)
+    merge(nums, start, mid, end)
+
+
+def merge(nums, start, mid, end):
+    global inversion_num
+    i = start
+    j = mid+1
+    tmp = []
+    while i <= mid and j <= end:
+        if nums[i] <= nums[j]:
+            inversion_num += j - mid - 1
+            tmp.append(nums[i])
+            i += 1
+        else:
+            tmp.append(nums[j])
+            j += 1
+
+    while i <= mid:
+        # 这时nums[i]的逆序数是整个nums[mid+1: end+1]的长度
+        inversion_num += end - mid
+        tmp.append(nums[i])
+        i += 1
+
+    while j <= end:
+        tmp.append(nums[j])
+        j += 1
+
+    nums[start: end+1] = tmp
+
+
+if __name__ == '__main__':
+    print('--- count inversion number using merge sort ---')
+    # nums = [5, 0, 4, 2, 3, 1, 6, 8, 7]
+    nums = [5, 0, 4, 2, 3, 1, 3, 3, 3, 6, 8, 7]
+    print('nums  : {}'.format(nums))
+    merge_sort_counting(nums, 0, len(nums)-1)
+    print('sorted: {}'.format(nums))
+    print('inversion number: {}'.format(inversion_num))

python/39_back_track/01_bag.py

@@ -0,0 +1,59 @@
+#!/usr/bin/python
+# -*- coding: UTF-8 -*-
+
+from typing import List
+
+# 背包选取的物品列表
+picks = []
+picks_with_max_value = []
+
+
+def bag(capacity: int, cur_weight: int, items_info: List, pick_idx: int):
+    """
+    回溯法解01背包，穷举
+    :param capacity: 背包容量
+    :param cur_weight: 背包当前重量
+    :param items_info: 物品的重量和价值信息
+    :param pick_idx: 当前物品的索引
+    :return:
+    """
+    # 考察完所有物品，或者在中途已经装满
+    if pick_idx >= len(items_info) or cur_weight == capacity:
+        global picks_with_max_value
+        if get_value(items_info, picks) > \
+                get_value(items_info, picks_with_max_value):
+            picks_with_max_value = picks.copy()
+    else:
+        item_weight = items_info[pick_idx][0]
+        if cur_weight + item_weight <= capacity:    # 选
+            picks[pick_idx] = 1
+            bag(capacity, cur_weight + item_weight, items_info, pick_idx + 1)
+
+        picks[pick_idx] = 0                         # 不选
+        bag(capacity, cur_weight, items_info, pick_idx + 1)
+
+
+def get_value(items_info: List, pick_items: List):
+    values = [_[1] for _ in items_info]
+    return sum([a*b for a, b in zip(values, pick_items)])
+
+
+if __name__ == '__main__':
+    # [(weight, value), ...]
+    items_info = [(3, 5), (2, 2), (1, 4), (1, 2), (4, 10)]
+    capacity = 8
+
+    print('--- items info ---')
+    print(items_info)
+
+    print('\n--- capacity ---')
+    print(capacity)
+
+    picks = [0] * len(items_info)
+    bag(capacity, 0, items_info, 0)
+
+    print('\n--- picks ---')
+    print(picks_with_max_value)
+
+    print('\n--- value ---')
+    print(get_value(items_info, picks_with_max_value))

python/39_back_track/eight_queens.py

@@ -0,0 +1,57 @@
+#!/usr/bin/python
+# -*- coding: UTF-8 -*-
+
+# 棋盘尺寸
+BOARD_SIZE = 8
+
+solution_count = 0
+queen_list = [0] * BOARD_SIZE
+
+
+def eight_queens(cur_column: int):
+    """
+    输出所有符合要求的八皇后序列
+    用一个长度为8的数组代表棋盘的列，数组的数字则为当前列上皇后所在的行数
+    :return:
+    """
+    if cur_column >= BOARD_SIZE:
+        global solution_count
+        solution_count += 1
+        # 解
+        print(queen_list)
+    else:
+        for i in range(BOARD_SIZE):
+            if is_valid_pos(cur_column, i):
+                queen_list[cur_column] = i
+                eight_queens(cur_column + 1)
+
+
+def is_valid_pos(cur_column: int, pos: int) -> bool:
+    """
+    因为采取的是每列放置1个皇后的做法
+    所以检查的时候不必检查列的合法性，只需要检查行和对角
+    1. 行：检查数组在下标为cur_column之前的元素是否已存在pos
+    2. 对角：检查数组在下标为cur_column之前的元素，其行的间距pos - QUEEN_LIST[i]
+       和列的间距cur_column - i是否一致
+    :param cur_column:
+    :param pos:
+    :return:
+    """
+    i = 0
+    while i < cur_column:
+        # 同行
+        if queen_list[i] == pos:
+            return False
+        # 对角线
+        if cur_column - i == abs(pos - queen_list[i]):
+            return False
+        i += 1
+    return True
+
+
+if __name__ == '__main__':
+    print('--- eight queens sequence ---')
+    eight_queens(0)
+
+    print('\n--- solution count ---')
+    print(solution_count)

python/39_back_track/permutations.py

@@ -0,0 +1,42 @@
+#!/usr/bin/python
+# -*- coding: UTF-8 -*-
+
+from typing import List
+
+permutations_list = []  # 全局变量，用于记录每个输出
+
+
+def permutations(nums: List, n: int, pick_count: int):
+    """
+    从nums选取n个数的全排列
+
+    回溯法，用一个栈记录当前路径信息
+    当满足n==0时，说明栈中的数已足够，输出并终止遍历
+    :param nums:
+    :param n:
+    :param pick_count:
+    :return:
+    """
+    if n == 0:
+        print(permutations_list)
+    else:
+        for i in range(len(nums) - pick_count):
+            permutations_list[pick_count] = nums[i]
+            nums[i], nums[len(nums) - pick_count - 1] = nums[len(nums) - pick_count - 1], nums[i]
+            permutations(nums, n-1, pick_count+1)
+            nums[i], nums[len(nums) - pick_count - 1] = nums[len(nums) - pick_count - 1], nums[i]
+
+
+if __name__ == '__main__':
+    nums = [1, 2, 3, 4]
+    n = 3
+    print('--- list ---')
+    print(nums)
+
+    print('\n--- pick num ---')
+    print(n)
+
+    print('\n--- permutation list ---')
+    permutations_list = [0] * n
+    permutations(nums, n, 0)
+

python/39_back_track/regex.py

@@ -0,0 +1,35 @@
+#!/usr/bin/python
+# -*- coding: UTF-8 -*-
+
+is_match = False
+
+
+def rmatch(r_idx: int, m_idx: int, regex: str, main: str):
+    global is_match
+    if is_match:
+        return
+
+    if r_idx >= len(regex):     # 正则串全部匹配好了
+        is_match = True
+        return
+
+    if m_idx >= len(main) and r_idx < len(regex):   # 正则串没匹配完，但是主串已经没得匹配了
+        is_match = False
+        return
+
+    if regex[r_idx] == '*':     # * 匹配1个或多个任意字符，递归搜索每一种情况
+        for i in range(m_idx, len(main)):
+            rmatch(r_idx+1, i+1, regex, main)
+    elif regex[r_idx] == '?':   # ? 匹配0个或1个任意字符，两种情况
+        rmatch(r_idx+1, m_idx+1, regex, main)
+        rmatch(r_idx+1, m_idx, regex, main)
+    else:                       # 非特殊字符需要精确匹配
+        if regex[r_idx] == main[m_idx]:
+            rmatch(r_idx+1, m_idx+1, regex, main)
+
+
+if __name__ == '__main__':
+    regex = 'ab*eee?d'
+    main = 'abcdsadfkjlekjoiwjiojieeecd'
+    rmatch(0, 0, regex, main)
+    print(is_match)

python/39_backtracking/backtracking.py

@@ -0,0 +1,25 @@
+"""
+    Author: Wenru Dong
+"""
+
+from typing import List
+
+def eight_queens() -> None:
+    solutions = []
+
+    def backtracking(queens_at_column: List[int], index_sums: List[int], index_diffs: List[int]) -> None:
+        row = len(queens_at_column)
+        if row == 8:
+            solutions.append(queens_at_column)
+            return
+        for col in range(8):
+            if col in queens_at_column or row + col in index_sums or row - col in index_diffs: continue
+            backtracking(queens_at_column + [col], index_sums + [row + col], index_diffs + [row - col])
+    
+    backtracking([], [], [])
+    print(*(" " + " ".join("*" * i + "Q" + "*" * (8 - i - 1) + "\n" for i in solution) for solution in solutions), sep="\n")
+
+
+if __name__ == "__main__":
+
+    eight_queens()