Algorithms/algo
1
0
Fork 0
Code Issues Pull Requests Actions Packages Projects Releases Wiki Activity

[notes][17_skiplist] complexity analytics.

Browse Source
This commit is contained in:
Liam Huang 2018-10-29 10:46:55 +08:00
parent 4038c72fe3
commit 9a3e148b11
No known key found for this signature in database
GPG Key ID: 4CA29EEF7482C289
1 changed files with 9 additions and 0 deletions
Show Stats Download Patch File Download Diff File Expand all files Collapse all files

9
notes/17_skiplist/readme.md
View File

@ -21,3 +21,12 @@
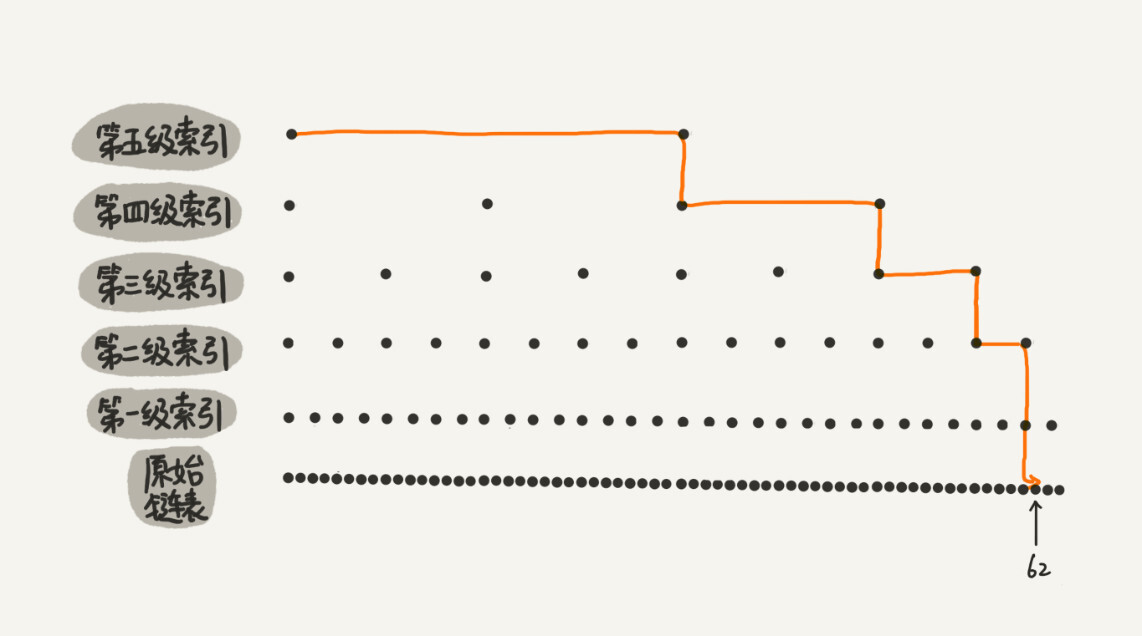
例如对于一个具有 64 个有序元素的五级跳表，查找起来的过程大约如下图所示。
![五级跳表示例](https://static001.geekbang.org/resource/image/46/a9/46d283cd82c987153b3fe0c76dfba8a9.jpg)
## 复杂度分析
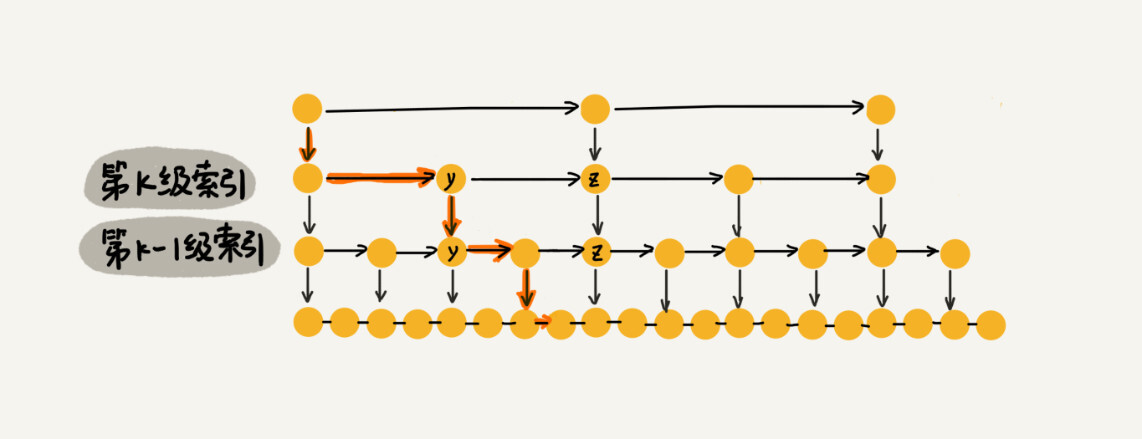
对于一个每一级索引的跨度是下一级索引 $k$ 倍的跳表，每一次 `down` 操作，相当于将搜索范围缩小到「剩余的可能性的 $1 / k$」。因此，查找具体某个元素的时间复杂度大约需要 $\lfloor \log_k n\rfloor + 1$ 次操作；也就是说时间复杂度是 $O(\log n)$。
![跳表查询过程示例](https://static001.geekbang.org/resource/image/d0/0c/d03bef9a64a0368e6a0d23ace8bd450c.jpg)
前面说了，跳表是一种用空间换时间的数据结构。因此它的空间复杂度一定不小。我们考虑原链表有 $n$ 个元素，那么第一级索引就有 $n / k$ 个元素，剩余的索引依次有 $n / k^2$, $n / k^3$, ..., $1$ 个元素。总共的元素个数是一个等比数列求和问题，它的值是 $\frac{n - 1}{k - 1}$。可见，不论 $k$ 是多少，跳表的空间复杂度都是 $O(n)$；但随着 $k$ 的增加，实际需要的额外节点数会下降。