commit
d6aa5b8c6e
281
c-cpp/06_linkedlist/singlelist_gc/singleList.c
Normal file
281
c-cpp/06_linkedlist/singlelist_gc/singleList.c
Normal file
@ -0,0 +1,281 @@
|
||||
#include "singleList.h"
|
||||
|
||||
#include <string.h>
|
||||
|
||||
linkedList * listCreate()
|
||||
{
|
||||
linkedList *list = NULL;
|
||||
list = malloc(sizeof(*list));
|
||||
if (NULL == list)
|
||||
{
|
||||
return NULL;
|
||||
}
|
||||
|
||||
list->dup = NULL;
|
||||
list->free = NULL;
|
||||
list->match = NULL;
|
||||
|
||||
list->head = NULL;
|
||||
list->len = 0;
|
||||
|
||||
return list;
|
||||
}
|
||||
|
||||
// 释放
|
||||
void listRelease(linkedList *list)
|
||||
{
|
||||
if (NULL == list)
|
||||
{
|
||||
return;
|
||||
}
|
||||
|
||||
listEmpty(list);
|
||||
|
||||
free(list);
|
||||
list = NULL;
|
||||
}
|
||||
|
||||
void listEmpty(linkedList *list)
|
||||
{
|
||||
if (NULL == list)
|
||||
{
|
||||
return;
|
||||
}
|
||||
|
||||
while (NULL != list->head)
|
||||
{
|
||||
listNode *pNode = list->head;
|
||||
list->head = pNode->next;
|
||||
if (NULL != list->free)
|
||||
{
|
||||
list->free(pNode->value);
|
||||
}
|
||||
else
|
||||
{
|
||||
free(pNode->value);
|
||||
}
|
||||
|
||||
pNode->next = NULL;
|
||||
free(pNode);
|
||||
pNode = NULL;
|
||||
}
|
||||
}
|
||||
|
||||
linkedList * listAddNodeHead(linkedList *list, void * value)
|
||||
{
|
||||
if (NULL == list || NULL == value)
|
||||
{
|
||||
return list;
|
||||
}
|
||||
|
||||
listNode *node = NULL;
|
||||
node = malloc(sizeof(*node));
|
||||
if (NULL == node)
|
||||
{
|
||||
return list;
|
||||
}
|
||||
|
||||
node->value = value;
|
||||
node->next = list->head;
|
||||
list->head = node;
|
||||
|
||||
++list->len;
|
||||
return list;
|
||||
}
|
||||
|
||||
linkedList * listAddNodeTail(linkedList *list, void *value)
|
||||
{
|
||||
if (NULL == list || NULL == value)
|
||||
{
|
||||
return list;
|
||||
}
|
||||
|
||||
listNode *node = NULL;
|
||||
node = malloc(sizeof(*node));
|
||||
if (NULL == node)
|
||||
{
|
||||
return list;
|
||||
}
|
||||
|
||||
node->value = value;
|
||||
node->next = NULL;
|
||||
|
||||
if (NULL == list->head
|
||||
&& list->len == 0)
|
||||
{
|
||||
list->head = node;
|
||||
}
|
||||
else
|
||||
{
|
||||
listNode *tail = list->head;
|
||||
listNode *pre = list->head;
|
||||
while (NULL != tail)
|
||||
{
|
||||
pre = tail;
|
||||
tail = tail->next;
|
||||
}
|
||||
|
||||
pre->next = node;
|
||||
}
|
||||
|
||||
++list->len;
|
||||
return list;
|
||||
}
|
||||
|
||||
linkedList * listInsertNode(linkedList *list, listNode *old_node, void *value, bool after)
|
||||
{
|
||||
if (NULL == list || NULL == old_node)
|
||||
{
|
||||
return list;
|
||||
}
|
||||
|
||||
listNode *pNode = NULL;
|
||||
pNode = malloc(sizeof(*pNode));
|
||||
if (NULL == pNode)
|
||||
{
|
||||
return list;
|
||||
}
|
||||
|
||||
pNode->value = value;
|
||||
if (after)
|
||||
{
|
||||
pNode->next = old_node->next;
|
||||
old_node->next = pNode;
|
||||
}
|
||||
else
|
||||
{
|
||||
listNode *pre = list->head;
|
||||
while (pre->next != old_node)
|
||||
{
|
||||
pre = pre->next;
|
||||
}
|
||||
|
||||
if (NULL != pre)
|
||||
{
|
||||
pre->next = pNode;
|
||||
pNode->next = old_node;
|
||||
}
|
||||
}
|
||||
|
||||
++list->len;
|
||||
return list;
|
||||
}
|
||||
|
||||
// 没设置释放函数时不做释放处理
|
||||
void listDelNode(linkedList *list, listNode *node)
|
||||
{
|
||||
if (NULL == list || NULL == node)
|
||||
{
|
||||
return;
|
||||
}
|
||||
|
||||
listNode *pre = list->head;
|
||||
listNode *cur = list->head;
|
||||
while (NULL != cur && cur != node)
|
||||
{
|
||||
pre = cur;
|
||||
cur = cur->next;
|
||||
}
|
||||
|
||||
// 不在该链表中
|
||||
if (NULL == pre)
|
||||
{
|
||||
return;
|
||||
}
|
||||
|
||||
pre->next = node->next;
|
||||
node->next = NULL;
|
||||
--list->len;
|
||||
|
||||
if (NULL != list->free)
|
||||
{
|
||||
list->free(node->value);
|
||||
free(node);
|
||||
node = NULL;
|
||||
}
|
||||
}
|
||||
|
||||
listNode * listSearchKey(linkedList *list, void *key)
|
||||
{
|
||||
if (NULL == list)
|
||||
{
|
||||
return NULL;
|
||||
}
|
||||
|
||||
listNode *node = list->head;
|
||||
while (NULL != node)
|
||||
{
|
||||
if (NULL != list->match)
|
||||
{
|
||||
if (list->match(key, node->value) == 0)
|
||||
{
|
||||
return node;
|
||||
}
|
||||
}
|
||||
else
|
||||
{
|
||||
if (key == node->value)
|
||||
{
|
||||
return node;
|
||||
}
|
||||
}
|
||||
|
||||
node = node->next;
|
||||
}
|
||||
|
||||
return NULL;
|
||||
}
|
||||
|
||||
listNode * listIndex(linkedList *list, long index)
|
||||
{
|
||||
if (NULL == list)
|
||||
{
|
||||
return NULL;
|
||||
}
|
||||
|
||||
if (index <= 0
|
||||
|| index > list->len)
|
||||
{
|
||||
return NULL;
|
||||
}
|
||||
|
||||
listNode *pNode = list->head;
|
||||
for (long i = 0; i < index; ++i)
|
||||
{
|
||||
pNode = pNode->next;
|
||||
}
|
||||
|
||||
return pNode;
|
||||
}
|
||||
|
||||
linkedList* listRewind(linkedList *list)
|
||||
{
|
||||
if (NULL == list)
|
||||
{
|
||||
return NULL;
|
||||
}
|
||||
|
||||
listNode *head = list->head;
|
||||
listNode *pre = NULL;
|
||||
listNode *next = NULL;
|
||||
while (NULL != head)
|
||||
{
|
||||
next = head->next;
|
||||
head->next = pre;
|
||||
pre = head;
|
||||
head = next;
|
||||
}
|
||||
|
||||
list->head = pre;
|
||||
return list;
|
||||
}
|
||||
|
||||
size_t listLength(linkedList *list)
|
||||
{
|
||||
if (NULL == list)
|
||||
{
|
||||
return 0;
|
||||
}
|
||||
|
||||
return list->len;
|
||||
}
|
||||
46
c-cpp/06_linkedlist/singlelist_gc/singleList.h
Normal file
46
c-cpp/06_linkedlist/singlelist_gc/singleList.h
Normal file
@ -0,0 +1,46 @@
|
||||
#ifndef __SINGLELIST_H__
|
||||
#define __SINGLELIST_H__
|
||||
|
||||
#include <stdlib.h>
|
||||
#include <stdbool.h>
|
||||
|
||||
typedef struct listNode
|
||||
{
|
||||
struct listNode *next;
|
||||
void *value;
|
||||
}listNode;
|
||||
|
||||
typedef struct linkedList
|
||||
{
|
||||
listNode *head;
|
||||
size_t len;
|
||||
size_t typesize;
|
||||
|
||||
void(*dup)(void*, void*);
|
||||
int(*match)(void*, void*);
|
||||
void(*free)(void*);
|
||||
}linkedList;
|
||||
|
||||
#define listSetDupMethod(l,m) ((l)->dup = (m))
|
||||
#define listSetFreeMethod(l,m) ((l)->free = (m))
|
||||
#define listSetMatchMethod(l,m) ((l)->match = (m))
|
||||
|
||||
#define listGetDupMethod(l) ((l)->dup)
|
||||
#define listGetFree(l) ((l)->free)
|
||||
#define listGetMatchMethod(l) ((l)->match)
|
||||
|
||||
linkedList *listCreate();
|
||||
void listRelease(linkedList *list);
|
||||
void listEmpty(linkedList *list);
|
||||
linkedList *listAddNodeHead(linkedList *list, void *value);
|
||||
linkedList *listAddNodeTail(linkedList *list, void *value);
|
||||
linkedList *listInsertNode(linkedList *list, listNode *old_node, void *value, bool after);
|
||||
void listDelNode(linkedList *list, listNode *node);
|
||||
|
||||
listNode *listSearchKey(linkedList *list, void *key);
|
||||
listNode *listIndex(linkedList *list, long index);
|
||||
linkedList* listRewind(linkedList *list);
|
||||
|
||||
size_t listLength(linkedList *list);
|
||||
|
||||
#endif // !__SINGLELIST_H__
|
||||
@ -49,18 +49,31 @@ public class Sorts {
|
||||
// 选择排序,a表示数组,n表示数组大小
|
||||
public static void selectionSort(int[] a, int n) {
|
||||
if (n <= 1) return;
|
||||
<<<<<<< HEAD
|
||||
for (int i = 0; i < n; ++i) {
|
||||
// 查找最小值
|
||||
int minIndex = i;
|
||||
int minValue = a[i];
|
||||
for (int j = i; j < n; ++j) {
|
||||
if (a[j] < minValue) {
|
||||
minValue = a[j];
|
||||
=======
|
||||
for (int i = 0; i < n - 1; ++i) {
|
||||
// 查找最小值
|
||||
int minIndex = i;
|
||||
for (int j = i + 1; j < n; ++j) {
|
||||
if (a[j] < a[minIndex]) {
|
||||
>>>>>>> upstream/master
|
||||
minIndex = j;
|
||||
}
|
||||
}
|
||||
|
||||
<<<<<<< HEAD
|
||||
=======
|
||||
if (minIndex == i)
|
||||
continue;
|
||||
|
||||
>>>>>>> upstream/master
|
||||
// 交换
|
||||
int tmp = a[i];
|
||||
a[i] = a[minIndex];
|
||||
|
||||
@ -1,100 +1,100 @@
|
||||
# 排序(上)
|
||||
|
||||
| 排序算法 | 时间复杂度 | 是否基于比较 |
|
||||
|---------|----|----|
|
||||
| 冒泡、插入、选择 | $O(n^2)$ | [y] |
|
||||
| 快排、归并 | $O(n\log n)$ | [y] |
|
||||
| 桶、基数、计数 | $O(n) | [x] |
|
||||
|
||||
开篇问题:插入排序和冒泡排序的时间复杂度相同,都是 $O(n^2)$,在实际软件开发中,为什么我们更倾向于使用插入排序而不是冒泡排序?
|
||||
|
||||
## 如何分析「排序算法」?
|
||||
|
||||
### 算法执行效率
|
||||
|
||||
1. 最好、最坏、平均情况的时间复杂度
|
||||
2. 时间复杂度的系数、低阶、常数——在渐进复杂度相同的情况下,需要比较系数、低阶和常数
|
||||
3. 比较和交换(移动)的次数——基于比较的排序算法的两种基本操作
|
||||
|
||||
### 算法的内存消耗
|
||||
|
||||
是否为原地排序算法(In-place sort algorithm),即算法的空间复杂度是否为 $O(1)$。
|
||||
|
||||
### 排序的稳定性
|
||||
|
||||
经过排序算法处理后,值相同的元素,在原序列和排序后序列中的相对位置保持不变,则称该排序算法是稳定的。
|
||||
|
||||
> 待排序的 `item` 并不是简单的值,而是一个基于对象中的某个 `key` 进行排序时,排序的稳定性就有意义了。
|
||||
|
||||
## 冒泡排序
|
||||
|
||||
* 每次循环都从序列起始位置开始
|
||||
* 循环中的每个动作,都对比相邻两个元素的大小是否满足偏序要求,若不满足,则交换顺序
|
||||
|
||||

|
||||
|
||||
分析:
|
||||
|
||||
* 原地排序
|
||||
* 稳定排序(偏序关系是严格的偏序关系,如 `<` 或 `>`)
|
||||
* 时间复杂度
|
||||
* 最好 $O(n)$
|
||||
* 最坏 $O(n^2)$
|
||||
* 平均 $O(n^2)$
|
||||
|
||||
### 冒泡排序的平均时间复杂度非严格分析
|
||||
|
||||
* 有序度:序列中满足偏序关系的两两组合的元素对的个数
|
||||
* 满有序度:排序完成的序列的有序度,它等于 $n(n - 1) / 2$
|
||||
* 逆序度:序列中不满足偏序关系的亮亮组合的元素对的个数
|
||||
|
||||
显然,$\text{逆序度} = \text{满有序度} - \text{有序度}$。
|
||||
|
||||
在冒泡排序中,每产生一次「交换」操作,$\text{逆序度}--$。于是,平均情况下,需要 $n(n - 1)/4$ 次交换操作,它已经是 $O(n^2)$ 了。因此,尽管比较操作的数量会大于交换操作的数量,但我们依然能说,冒泡排序的平均时间复杂度是 $O(n^2)$。
|
||||
|
||||
> 分析过程不严格,但足够说明问题。
|
||||
|
||||
## 插入排序
|
||||
|
||||
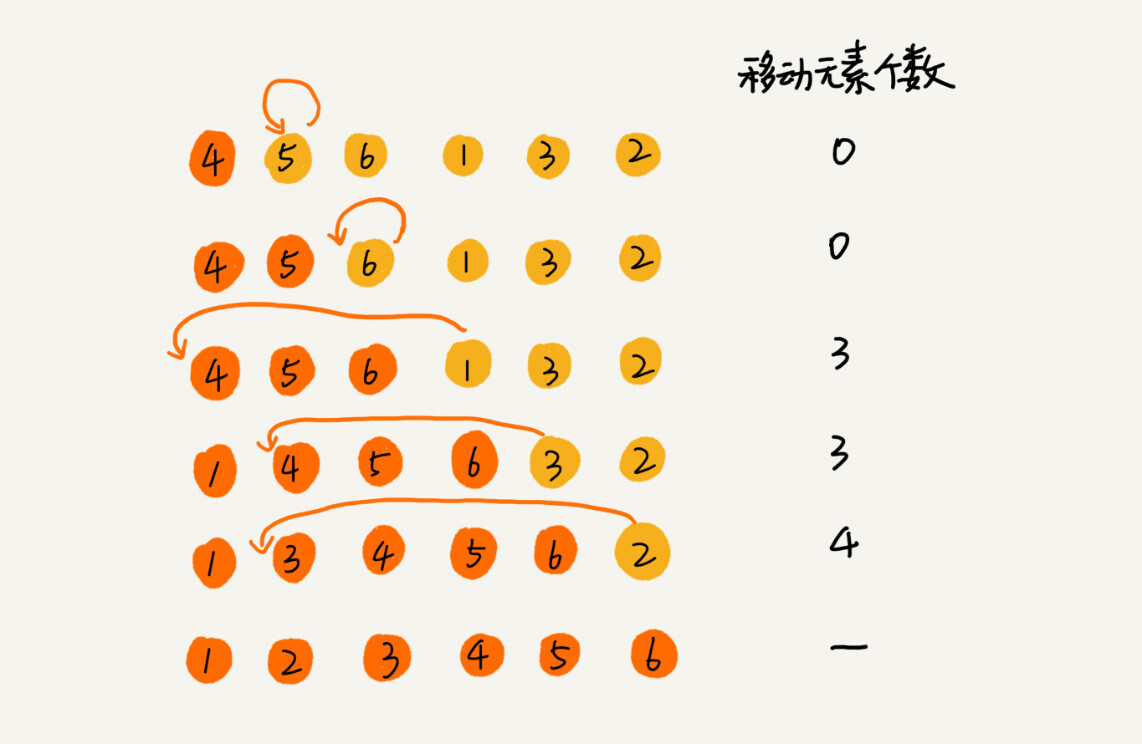
1. 将待排序数列分为已排序区间和未排序区间
|
||||
2. 取未排序区间的第一个元素
|
||||
3. 遍历已排序区间,按照偏序关系,寻找合适的位置,插入未排序区间的第一个元素
|
||||
4. 重复 2 -- 3 直至未排序区间长度为零
|
||||
|
||||
|
||||
|
||||
分析:
|
||||
|
||||
* 原地排序
|
||||
* 稳定排序(值相同的元素,往后插)
|
||||
* 时间复杂度
|
||||
* 最好 $O(n)$
|
||||
* 最坏 $O(n^2)$
|
||||
* 平均 $O(n^2)$(乘法法则)
|
||||
|
||||
## 选择排序
|
||||
|
||||
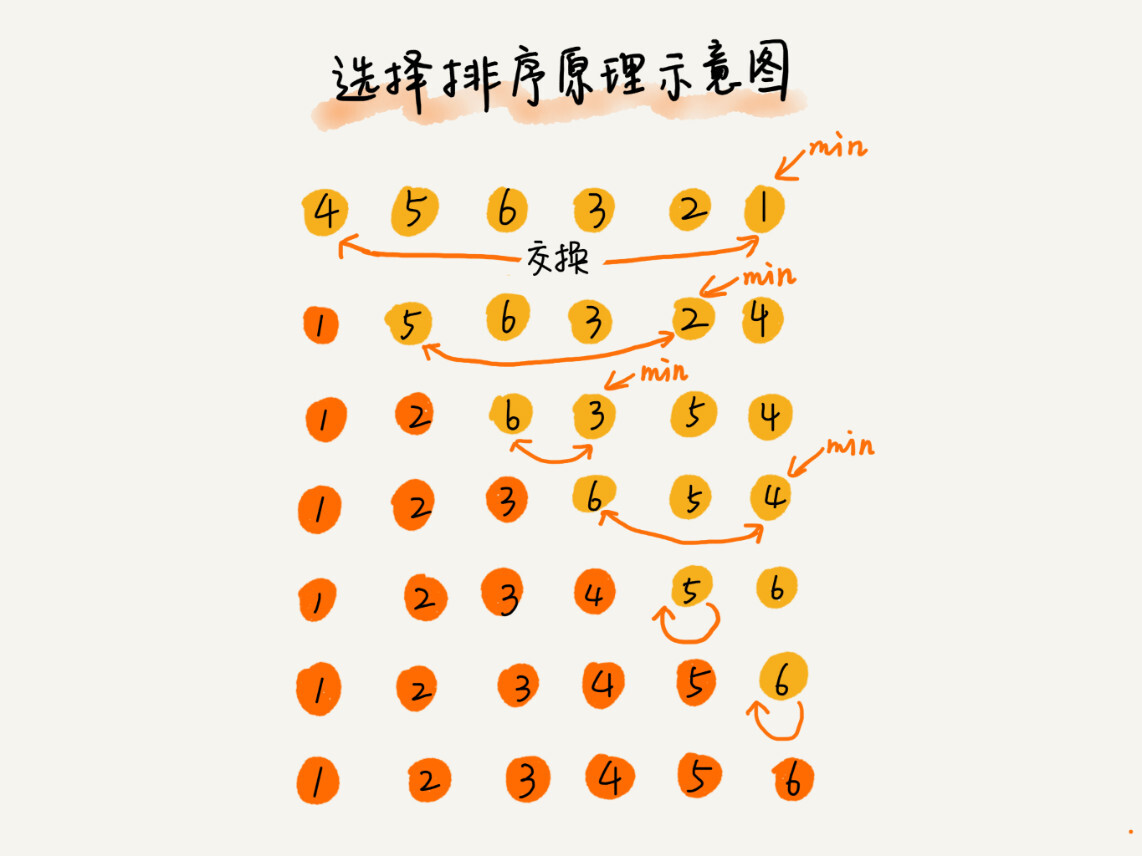
1. 将待排序数列分为已排序区间和未排序区间
|
||||
2. 遍历未排序区间,取未排序区间的最小元素
|
||||
3. 交换上述最小元素与未排序区间中的第一个元素的位置
|
||||
4. 重复 2 -- 3 直至未排序区间长度为零
|
||||
|
||||
|
||||
|
||||
分析:
|
||||
|
||||
* 非原地排序
|
||||
* 非稳定排序
|
||||
* 时间复杂度
|
||||
* 最好 $O(n^2)$
|
||||
* 最坏 $O(n^2)$
|
||||
* 平均 $O(n^2)$(乘法法则)
|
||||
|
||||
## 开篇问题
|
||||
|
||||
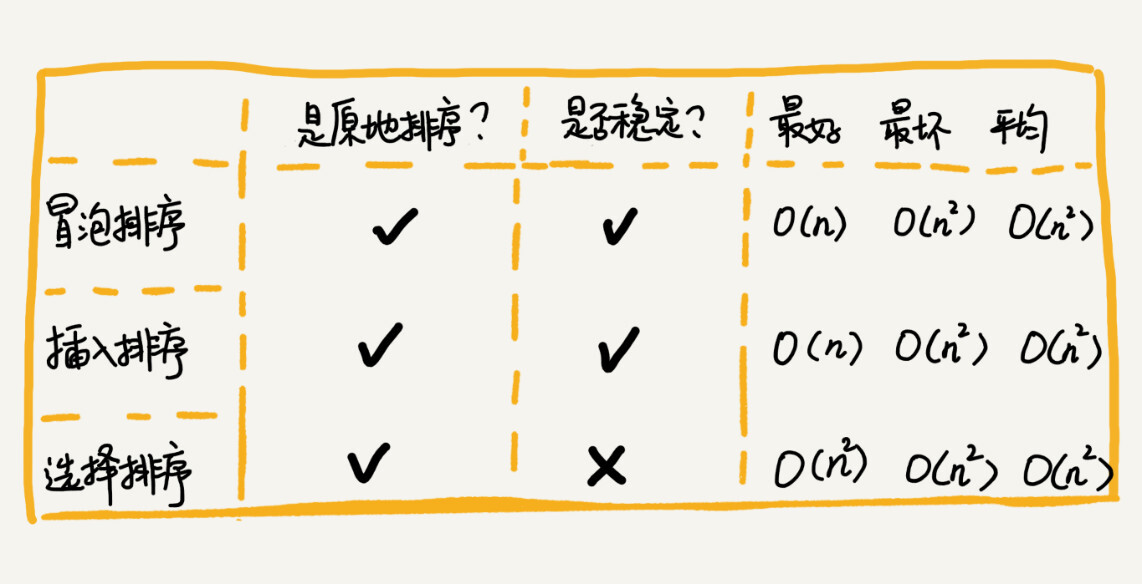
* 对同一份未排序序列数据,冒泡排序和插入排序所需的交换(移动)次数是一定的,且是相等的
|
||||
* 单次数据交换,冒泡排序所需的时间更长(三次赋值操作,插排只需要一次)
|
||||
|
||||
另有插入排序的优化版本[希尔排序](https://zh.wikipedia.org/wiki/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F)。
|
||||
|
||||
|
||||
# 排序(上)
|
||||
|
||||
| 排序算法 | 时间复杂度 | 是否基于比较 |
|
||||
|---------|----|----|
|
||||
| 冒泡、插入、选择 | $O(n^2)$ | [y] |
|
||||
| 快排、归并 | $O(n\log n)$ | [y] |
|
||||
| 桶、基数、计数 | $O(n) | [x] |
|
||||
|
||||
开篇问题:插入排序和冒泡排序的时间复杂度相同,都是 $O(n^2)$,在实际软件开发中,为什么我们更倾向于使用插入排序而不是冒泡排序?
|
||||
|
||||
## 如何分析「排序算法」?
|
||||
|
||||
### 算法执行效率
|
||||
|
||||
1. 最好、最坏、平均情况的时间复杂度
|
||||
2. 时间复杂度的系数、低阶、常数——在渐进复杂度相同的情况下,需要比较系数、低阶和常数
|
||||
3. 比较和交换(移动)的次数——基于比较的排序算法的两种基本操作
|
||||
|
||||
### 算法的内存消耗
|
||||
|
||||
是否为原地排序算法(In-place sort algorithm),即算法的空间复杂度是否为 $O(1)$。
|
||||
|
||||
### 排序的稳定性
|
||||
|
||||
经过排序算法处理后,值相同的元素,在原序列和排序后序列中的相对位置保持不变,则称该排序算法是稳定的。
|
||||
|
||||
> 待排序的 `item` 并不是简单的值,而是一个基于对象中的某个 `key` 进行排序时,排序的稳定性就有意义了。
|
||||
|
||||
## 冒泡排序
|
||||
|
||||
* 每次循环都从序列起始位置开始
|
||||
* 循环中的每个动作,都对比相邻两个元素的大小是否满足偏序要求,若不满足,则交换顺序
|
||||
|
||||

|
||||
|
||||
分析:
|
||||
|
||||
* 原地排序
|
||||
* 稳定排序(偏序关系是严格的偏序关系,如 `<` 或 `>`)
|
||||
* 时间复杂度
|
||||
* 最好 $O(n)$
|
||||
* 最坏 $O(n^2)$
|
||||
* 平均 $O(n^2)$
|
||||
|
||||
### 冒泡排序的平均时间复杂度非严格分析
|
||||
|
||||
* 有序度:序列中满足偏序关系的两两组合的元素对的个数
|
||||
* 满有序度:排序完成的序列的有序度,它等于 $n(n - 1) / 2$
|
||||
* 逆序度:序列中不满足偏序关系的亮亮组合的元素对的个数
|
||||
|
||||
显然,$\text{逆序度} = \text{满有序度} - \text{有序度}$。
|
||||
|
||||
在冒泡排序中,每产生一次「交换」操作,$\text{逆序度}--$。于是,平均情况下,需要 $n(n - 1)/4$ 次交换操作,它已经是 $O(n^2)$ 了。因此,尽管比较操作的数量会大于交换操作的数量,但我们依然能说,冒泡排序的平均时间复杂度是 $O(n^2)$。
|
||||
|
||||
> 分析过程不严格,但足够说明问题。
|
||||
|
||||
## 插入排序
|
||||
|
||||
1. 将待排序数列分为已排序区间和未排序区间
|
||||
2. 取未排序区间的第一个元素
|
||||
3. 遍历已排序区间,按照偏序关系,寻找合适的位置,插入未排序区间的第一个元素
|
||||
4. 重复 2 -- 3 直至未排序区间长度为零
|
||||
|
||||

|
||||
|
||||
分析:
|
||||
|
||||
* 原地排序
|
||||
* 稳定排序(值相同的元素,往后插)
|
||||
* 时间复杂度
|
||||
* 最好 $O(n)$
|
||||
* 最坏 $O(n^2)$
|
||||
* 平均 $O(n^2)$(乘法法则)
|
||||
|
||||
## 选择排序
|
||||
|
||||
1. 将待排序数列分为已排序区间和未排序区间
|
||||
2. 遍历未排序区间,取未排序区间的最小元素
|
||||
3. 交换上述最小元素与未排序区间中的第一个元素的位置
|
||||
4. 重复 2 -- 3 直至未排序区间长度为零
|
||||
|
||||

|
||||
|
||||
分析:
|
||||
|
||||
* 非原地排序
|
||||
* 非稳定排序
|
||||
* 时间复杂度
|
||||
* 最好 $O(n^2)$
|
||||
* 最坏 $O(n^2)$
|
||||
* 平均 $O(n^2)$(乘法法则)
|
||||
|
||||
## 开篇问题
|
||||
|
||||
* 对同一份未排序序列数据,冒泡排序和插入排序所需的交换(移动)次数是一定的,且是相等的
|
||||
* 单次数据交换,冒泡排序所需的时间更长(三次赋值操作,插排只需要一次)
|
||||
|
||||
另有插入排序的优化版本[希尔排序](https://zh.wikipedia.org/wiki/%E5%B8%8C%E5%B0%94%E6%8E%92%E5%BA%8F)。
|
||||
|
||||

|
||||
|
||||
@ -28,6 +28,8 @@ function expression($str)
|
||||
array_push($operStack, $arr[$i]);
|
||||
break;
|
||||
case '*':
|
||||
<<<<<<< HEAD
|
||||
=======
|
||||
$arrLen = count($operStack);
|
||||
while ($operStack[$arrLen-1] === '/'){
|
||||
compute($numStack, $operStack);
|
||||
@ -36,6 +38,7 @@ function expression($str)
|
||||
array_push($operStack, $arr[$i]);
|
||||
break;
|
||||
|
||||
>>>>>>> upstream/master
|
||||
case '/':
|
||||
case '(':
|
||||
array_push($operStack, $arr[$i]);
|
||||
@ -78,9 +81,13 @@ function compute(&$numStack, &$operStack){
|
||||
case '-':
|
||||
array_push($numStack, array_pop($numStack) - $num);
|
||||
break;
|
||||
<<<<<<< HEAD
|
||||
|
||||
=======
|
||||
case '(':
|
||||
throw new \Exception("不匹配的(", 2);
|
||||
break;
|
||||
>>>>>>> upstream/master
|
||||
}
|
||||
}
|
||||
expression('-1+2-(1+2*3)');
|
||||
|
||||
@ -17,7 +17,11 @@
|
||||
* findMiddleNode 求链表的中间结点
|
||||
|
||||
#### 08_stack
|
||||
<<<<<<< HEAD
|
||||
* 链栈实现
|
||||
=======
|
||||
* 链栈实现
|
||||
|
||||
#### 09_stack
|
||||
* 队列链表实现
|
||||
* 队列链表实现
|
||||
>>>>>>> upstream/master
|
||||
|
||||
78
php/Stack/Compute.php
Normal file
78
php/Stack/Compute.php
Normal file
@ -0,0 +1,78 @@
|
||||
<?php
|
||||
|
||||
|
||||
|
||||
// 四则运算 +-*/()
|
||||
function expression($str)
|
||||
{
|
||||
$str = str_replace(' ','',$str);
|
||||
$arr = preg_split('/([\+\-\*\/\(\)])/', $str, -1, PREG_SPLIT_DELIM_CAPTURE | PREG_SPLIT_NO_EMPTY);
|
||||
|
||||
$numStack = []; // 存放数字
|
||||
$operStack = []; // 存放运算符
|
||||
$operStack[] = NULL;
|
||||
|
||||
for ($i = 0; $i < count($arr); $i++){
|
||||
if (ord($arr[$i]) >= 48 && ord($arr[$i] <= 57)){
|
||||
array_push($numStack, $arr[$i]);
|
||||
continue;
|
||||
}
|
||||
switch ($arr[$i]){
|
||||
case '+':
|
||||
case '-':
|
||||
$arrLen = count($operStack);
|
||||
while ($operStack[$arrLen-1] === '*' || $operStack[$arrLen-1] === '/' || $operStack[$arrLen-1] === '-'){
|
||||
compute($numStack, $operStack);
|
||||
$arrLen--;
|
||||
}
|
||||
array_push($operStack, $arr[$i]);
|
||||
break;
|
||||
case '*':
|
||||
case '/':
|
||||
case '(':
|
||||
array_push($operStack, $arr[$i]);
|
||||
break;
|
||||
case ')':
|
||||
$arrLen = count($operStack);
|
||||
while ($operStack[$arrLen-1] !== '('){
|
||||
compute($numStack, $operStack);
|
||||
$arrLen--;
|
||||
}
|
||||
array_pop($operStack);
|
||||
break;
|
||||
default:
|
||||
throw new \Exception("不支持的运算符", 1);
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
$arrLen = count($operStack);
|
||||
while ($operStack[$arrLen-1] !== NULL){
|
||||
compute($numStack, $operStack);
|
||||
$arrLen--;
|
||||
}
|
||||
echo array_pop($numStack);
|
||||
}
|
||||
|
||||
//数字栈长度减一,运算符栈长度减一
|
||||
function compute(&$numStack, &$operStack){
|
||||
$num = array_pop($numStack);
|
||||
switch (array_pop($operStack)) {
|
||||
case '*':
|
||||
array_push($numStack, array_pop($numStack) * $num);
|
||||
break;
|
||||
case '/':
|
||||
array_push($numStack, array_pop($numStack) / $num);
|
||||
break;
|
||||
case '+':
|
||||
array_push($numStack, array_pop($numStack) + $num);
|
||||
break;
|
||||
case '-':
|
||||
array_push($numStack, array_pop($numStack) - $num);
|
||||
break;
|
||||
|
||||
}
|
||||
}
|
||||
expression('-1+2-(1+2*3)');
|
||||
echo PHP_EOL;
|
||||
eval('echo -1+2-(1+2*3);');
|
||||
@ -7,8 +7,12 @@
|
||||
"psr-4": {
|
||||
"Algo_06\\": "06_linkedlist/",
|
||||
"Algo_07\\": "07_linkedlist/",
|
||||
<<<<<<< HEAD
|
||||
"Algo_08\\": "08_stack/"
|
||||
=======
|
||||
"Algo_08\\": "08_stack/",
|
||||
"Algo_09\\": "09_queue/"
|
||||
>>>>>>> upstream/master
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
@ -79,6 +79,12 @@ if __name__ == "__main__":
|
||||
for i in range(6):
|
||||
a.insert_to_tail(i)
|
||||
|
||||
<<<<<<< HEAD
|
||||
a.delete(2)
|
||||
print(a)
|
||||
a.insert_to_tail(7)
|
||||
print(a)
|
||||
=======
|
||||
print('origin',a)
|
||||
a.delete(4)
|
||||
print ('delete ',a)
|
||||
@ -86,3 +92,4 @@ if __name__ == "__main__":
|
||||
a.insert(100,10000)
|
||||
print (a)
|
||||
|
||||
>>>>>>> upstream/master
|
||||
|
||||
@ -21,7 +21,11 @@ class ArrayQueue:
|
||||
return False
|
||||
else:
|
||||
for i in range(0, self._tail - self._head):
|
||||
<<<<<<< HEAD
|
||||
self._data[i] = self._items[i + self._head]
|
||||
=======
|
||||
self._items[i] = self._items[i + self._head]
|
||||
>>>>>>> upstream/master
|
||||
self._tail = self._tail - self._head
|
||||
self._head = 0
|
||||
|
||||
|
||||
@ -11,8 +11,13 @@ from typing import List
|
||||
def bubble_sort(a: List[int]):
|
||||
if len(a) <= 1: return
|
||||
|
||||
<<<<<<< HEAD
|
||||
made_swap = False
|
||||
for i in range(len(a)):
|
||||
=======
|
||||
for i in range(len(a)):
|
||||
made_swap = False
|
||||
>>>>>>> upstream/master
|
||||
for j in range(len(a) - i - 1):
|
||||
if a[j] > a[j+1]:
|
||||
a[j], a[j+1] = a[j+1], a[j]
|
||||
|
||||
Loading…
Reference in New Issue
Block a user