commit
da58c9a34b
@ -1,4 +1,4 @@
|
||||
# 排序(上)
|
||||
# 排序(平方时间复杂度排序算法)
|
||||
|
||||
| 排序算法 | 时间复杂度 | 是否基于比较 |
|
||||
|---------|----|----|
|
||||
|
||||
0
notes/12_sorts/.gitkeep
Normal file
0
notes/12_sorts/.gitkeep
Normal file
176
notes/12_sorts/readme.md
Normal file
176
notes/12_sorts/readme.md
Normal file
@ -0,0 +1,176 @@
|
||||
# 排序(线性对数时间复杂度排序算法)
|
||||
|
||||
开篇问题:如何在 $O(n)$ 时间复杂度内寻找一个无序数组中第 K 大的元素?
|
||||
|
||||
## 归并排序
|
||||
|
||||
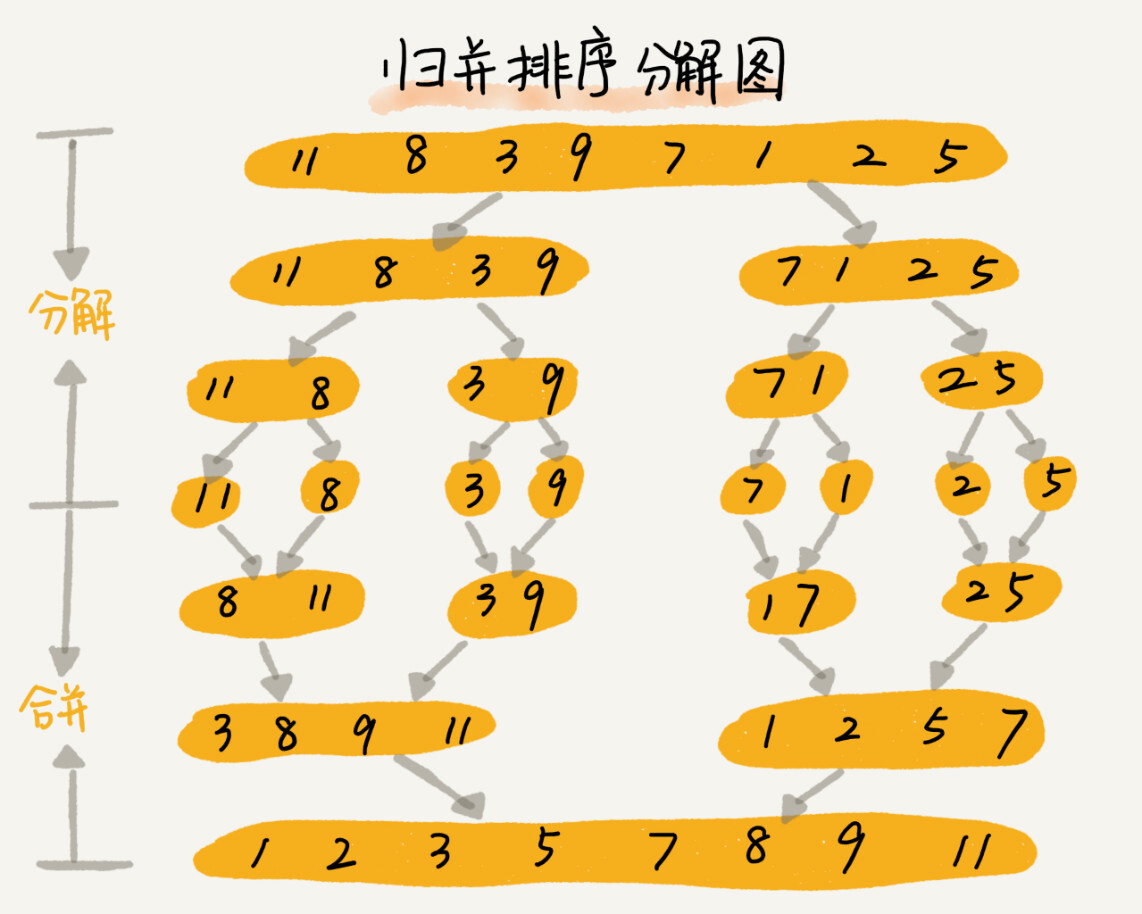
* 归并排序使用了「分治」思想(Divide and Conquer)
|
||||
* 分:把数组分成前后两部分,分别排序
|
||||
* 合:将有序的两部分合并
|
||||
|
||||
|
||||
|
||||
* 分治与递归
|
||||
* 分治:解决问题的处理办法
|
||||
* 递归:实现算法的手段
|
||||
* ——分治算法经常用递归来实现
|
||||
* 递归实现:
|
||||
* 终止条件:区间 `[first, last)` 内不足 2 个元素
|
||||
* 递归公式:`merge_sort(first, last) = merge(merge_sort(first, mid), merge_sort(mid, last))`,其中 `mid = first + (last - first) / 2`
|
||||
|
||||
C++ 实现:
|
||||
|
||||
```cpp
|
||||
template <typename FrwdIt,
|
||||
typename T = typename std::iterator_traits<FrwdIt>::value_type,
|
||||
typename BinaryPred = std::less<T>>
|
||||
void merge_sort(FrwdIt first, FrwdIt last, BinaryPred comp = BinaryPred()) {
|
||||
const auto len = std::distance(first, last);
|
||||
if (len <= 1) { return; }
|
||||
auto cut = first + len / 2;
|
||||
merge_sort(first, cut, comp);
|
||||
merge_sort(cut, last, comp);
|
||||
std::vector<T> tmp;
|
||||
tmp.reserve(len);
|
||||
detail::merge(first, cut, cut, last, std::back_inserter(tmp), comp);
|
||||
std::copy(tmp.begin(), tmp.end(), first);
|
||||
}
|
||||
```
|
||||
|
||||
这里涉及到一个 `merge` 的过程,它的实现大致是:
|
||||
|
||||
```cpp
|
||||
namespace detail {
|
||||
template <typename InputIt1, typename InputIt2, typename OutputIt,
|
||||
typename BinaryPred = std::less<typename std::iterator_traits<InputIt1>::value_type>>
|
||||
OutputIt merge(InputIt1 first1, InputIt1 last1,
|
||||
InputIt2 first2, InputIt2 last2,
|
||||
OutputIt d_first,
|
||||
BinaryPred comp = BinaryPred()) {
|
||||
for (; first1 != last1; ++d_first) {
|
||||
if (first2 == last2) {
|
||||
return std::copy(first1, last1, d_first);
|
||||
}
|
||||
if (comp(*first2, *first1)) {
|
||||
*d_first = *first2;
|
||||
++first2;
|
||||
} else {
|
||||
*d_first = *first1;
|
||||
++first1;
|
||||
}
|
||||
}
|
||||
return std::copy(first2, last2, d_first);
|
||||
}
|
||||
} // namespace detail
|
||||
```
|
||||
|
||||
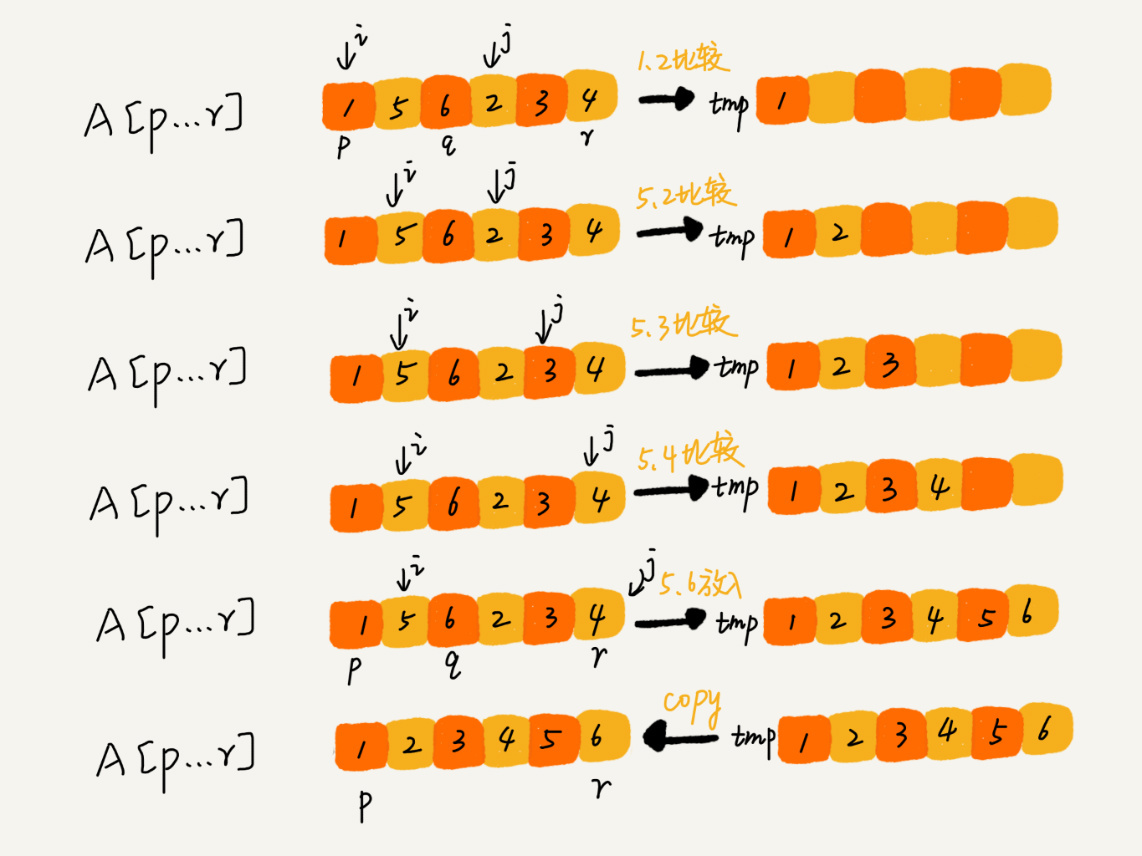
|
||||
|
||||
### 算法分析
|
||||
|
||||
* 稳定性
|
||||
* 由于 `comp` 是严格偏序,所以 `!comp(*first2, *first1)` 时,取用 `first1` 的元素放入 `d_first` 保证了算法稳定性
|
||||
* 时间复杂度
|
||||
* 定义 $T(n)$ 表示问题规模为 $n$ 时算法的耗时,
|
||||
* 有递推公式:$T(n) = 2T(n/2) + n$
|
||||
* 展开得 $T(n) = 2^{k}T(1) + k * n$
|
||||
* 考虑 $k$ 是递归深度,它的值是 $\log_2 n$,因此 $T(n) = n + n\log_2 n$
|
||||
* 因此,归并排序的时间复杂度为 $\Theta(n\log n)$
|
||||
* 空间复杂度
|
||||
* 一般来说,空间复杂度是 $\Theta(n)$
|
||||
|
||||
## 快速排序(quick sort,快排)
|
||||
|
||||
原理:
|
||||
|
||||
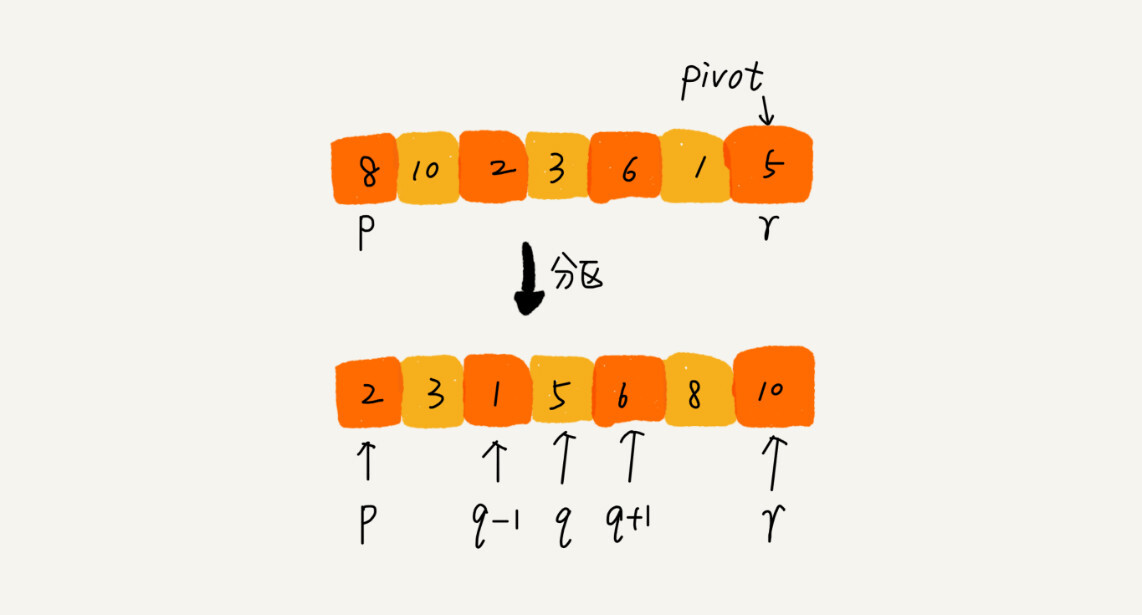
* 在待排序区间 `[first, last)` 中选取一个元素,称为主元(pivot,枢轴)
|
||||
* 对待排序区间进行划分,使得 `[first, cut)` 中的元素满足 `comp(element, pivot)` 而 `[cut, last)` 中的元素不满足 `comp(element, pivot)`
|
||||
* 对划分的两个区间,继续划分,直到区间 `[first, last)` 内不足 2 个元素
|
||||
|
||||
|
||||
|
||||
显然,这又是一个递归:
|
||||
|
||||
* 终止条件:区间 `[first, last)` 内不足 2 个元素
|
||||
* 递归公式:`quick_sort(first, last) = quick_sort(first, cut) + quick_sort(cut, last)`
|
||||
|
||||
```cpp
|
||||
template <typename IterT, typename T = typename std::iterator_traits<IterT>::value_type>
|
||||
void quick_sort(IterT first, IterT last) {
|
||||
if (std::distance(first, last) > 1) {
|
||||
IterT prev_last = std::prev(last);
|
||||
IterT cut = std::partition(first, prev_last, [prev_last](T v) { return v < *prev_last; });
|
||||
std::iter_swap(cut, prev_last);
|
||||
quick_sort(first, cut);
|
||||
quick_sort(cut, last);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
> 一点优化(Liam Huang):通过将 `if` 改为 `while` 同时修改 `last` 迭代器的值,可以节省一半递归调用的开销。
|
||||
|
||||
```cpp
|
||||
template <typename IterT, typename T = typename std::iterator_traits<IterT>::value_type>
|
||||
void quick_sort(IterT first, IterT last) {
|
||||
while (std::distance(first, last) > 1) {
|
||||
IterT prev_last = std::prev(last);
|
||||
IterT cut = std::partition(first, prev_last, [prev_last](T v) { return v < *prev_last; });
|
||||
std::iter_swap(cut, prev_last);
|
||||
quick_sort(cut, last);
|
||||
last = cut;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
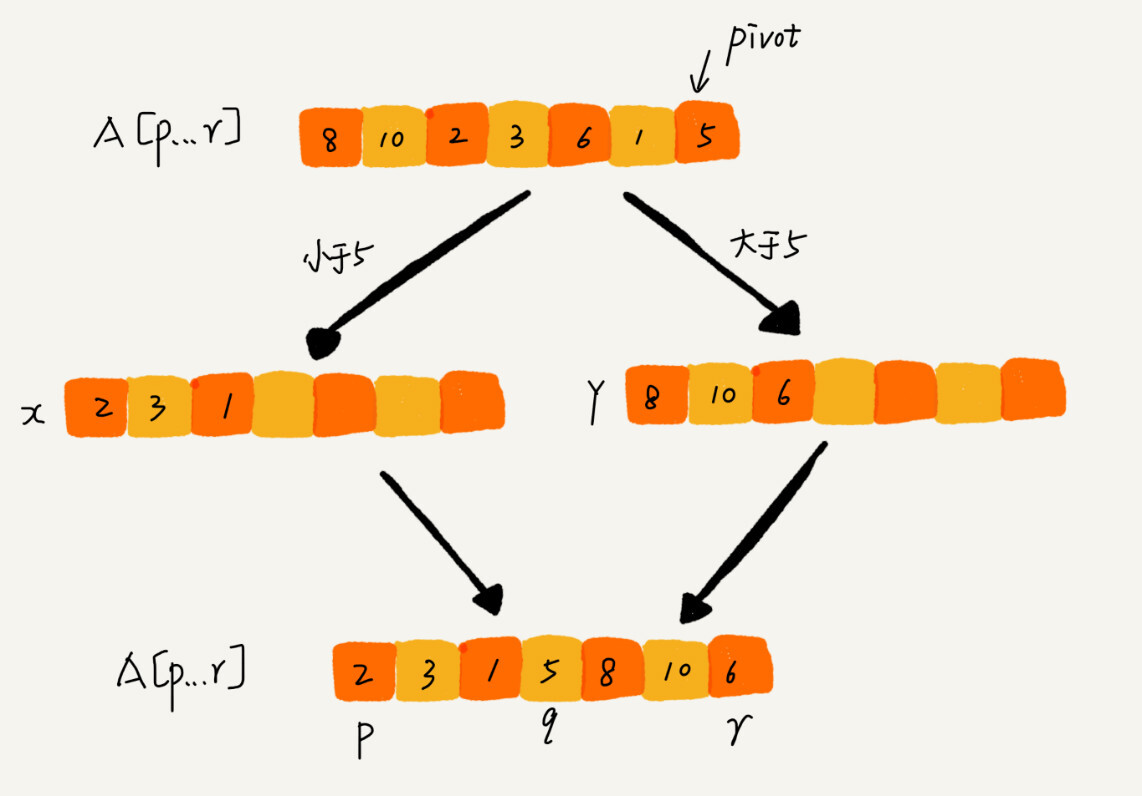
如果不要求空间复杂度,分区函数实现起来很容易。
|
||||
|
||||
|
||||
|
||||
若要求原地分区,则不那么容易了。下面的实现实现了原地分区函数,并且能将所有相等的主元排在一起。
|
||||
|
||||
```cpp
|
||||
template <typename BidirIt,
|
||||
typename T = typename std::iterator_traits<BidirIt>::value_type,
|
||||
typename Compare = std::less<T>>
|
||||
std::pair<BidirIt, BidirIt> inplace_partition(BidirIt first,
|
||||
BidirIt last,
|
||||
const T& pivot,
|
||||
Compare comp = Compare()) {
|
||||
BidirIt last_less, last_greater, first_equal, last_equal;
|
||||
for (last_less = first, last_greater = first, first_equal = last;
|
||||
last_greater != first_equal; ) {
|
||||
if (comp(*last_greater, pivot)) {
|
||||
std::iter_swap(last_greater++, last_less++);
|
||||
} else if (comp(pivot, *last_greater)) {
|
||||
++last_greater;
|
||||
} else { // pivot == *last_greater
|
||||
std::iter_swap(last_greater, --first_equal);
|
||||
}
|
||||
}
|
||||
const auto cnt = std::distance(first_equal, last);
|
||||
std::swap_ranges(first_equal, last, last_less);
|
||||
first_equal = last_less;
|
||||
last_equal = first_equal + cnt;
|
||||
return {first_equal, last_equal};
|
||||
}
|
||||
```
|
||||
|
||||
### 算法分析
|
||||
|
||||
* 稳定性
|
||||
* 由于 `inplace_partition` 使用了大量 `std::iter_swap` 操作,所以不是稳定排序
|
||||
* 时间复杂度
|
||||
* 定义 $T(n)$ 表示问题规模为 $n$ 时算法的耗时,
|
||||
* 有递推公式:$T(n) = 2T(n/2) + n$(假定每次分割都是均衡分割)
|
||||
* 展开得 $T(n) = 2^{k}T(1) + k * n$
|
||||
* 考虑 $k$ 是递归深度,它的值是 $\log_2 n$,因此 $T(n) = n + n\log_2 n$
|
||||
* 因此,快速排序的时间复杂度为 $\Theta(n\log n)$
|
||||
* 空间复杂度
|
||||
* 一般来说,空间复杂度是 $\Theta(1)$,因此是原地排序算法
|
||||
|
||||
## 开篇问题
|
||||
|
||||
* 分区,看前半段元素数量
|
||||
* 前半段元素数量 < K,对后半段进行分区
|
||||
* 前半段元素数量 > K,对前半段进行分区
|
||||
* 前半段元素数量 = K,前半段末位元素即是所求
|
||||
0
notes/13_sorts/.gitkeep
Normal file
0
notes/13_sorts/.gitkeep
Normal file
77
notes/13_sorts/readme.md
Normal file
77
notes/13_sorts/readme.md
Normal file
@ -0,0 +1,77 @@
|
||||
# 线性排序
|
||||
|
||||
## 开篇问题
|
||||
|
||||
如何按年龄给 100 万用户排序?
|
||||
|
||||
## 桶排序(Bucket Sort)
|
||||
|
||||
算法思想:
|
||||
|
||||
* 按待排序数据的 key 分有序桶
|
||||
* 桶内排序
|
||||
* 有序桶依次输出
|
||||
|
||||

|
||||
|
||||
### 算法分析
|
||||
|
||||
* 时间复杂度 $O(n)$
|
||||
* $n$ 个元素,分 $m$ 个有序桶,每个桶里平均 $k = n / m$ 个元素
|
||||
* 桶内快排,复杂度 $O(k \log k)$,$m$ 个桶一共 $O(n \log k)$
|
||||
* 当 $m$ 接近 $n$,例如当 $k = 4$ 时,这个复杂度近似 $O(n)$
|
||||
* 使用条件
|
||||
* 数据易于分如有序桶
|
||||
* 数据在各个有序桶之间分布均匀
|
||||
* 适合外部排序——数据不全部载入磁盘
|
||||
|
||||
## 计数排序(Counting Sort)
|
||||
|
||||
计数排序可以视作是桶排序的一个特殊情况:
|
||||
|
||||
* 数据的取值范围很小
|
||||
* 每个分桶内的元素 key 值都一样
|
||||
|
||||
此时,由于分桶内的元素 key 值都一样,所以桶内的排序操作可以省略,以及桶的编号本身就能记录桶内元素的值。因此,算法只需遍历一遍所有的数据,统计每个取值上有多少元素即可。这个过程时间复杂度是 $O(n)$。
|
||||
|
||||
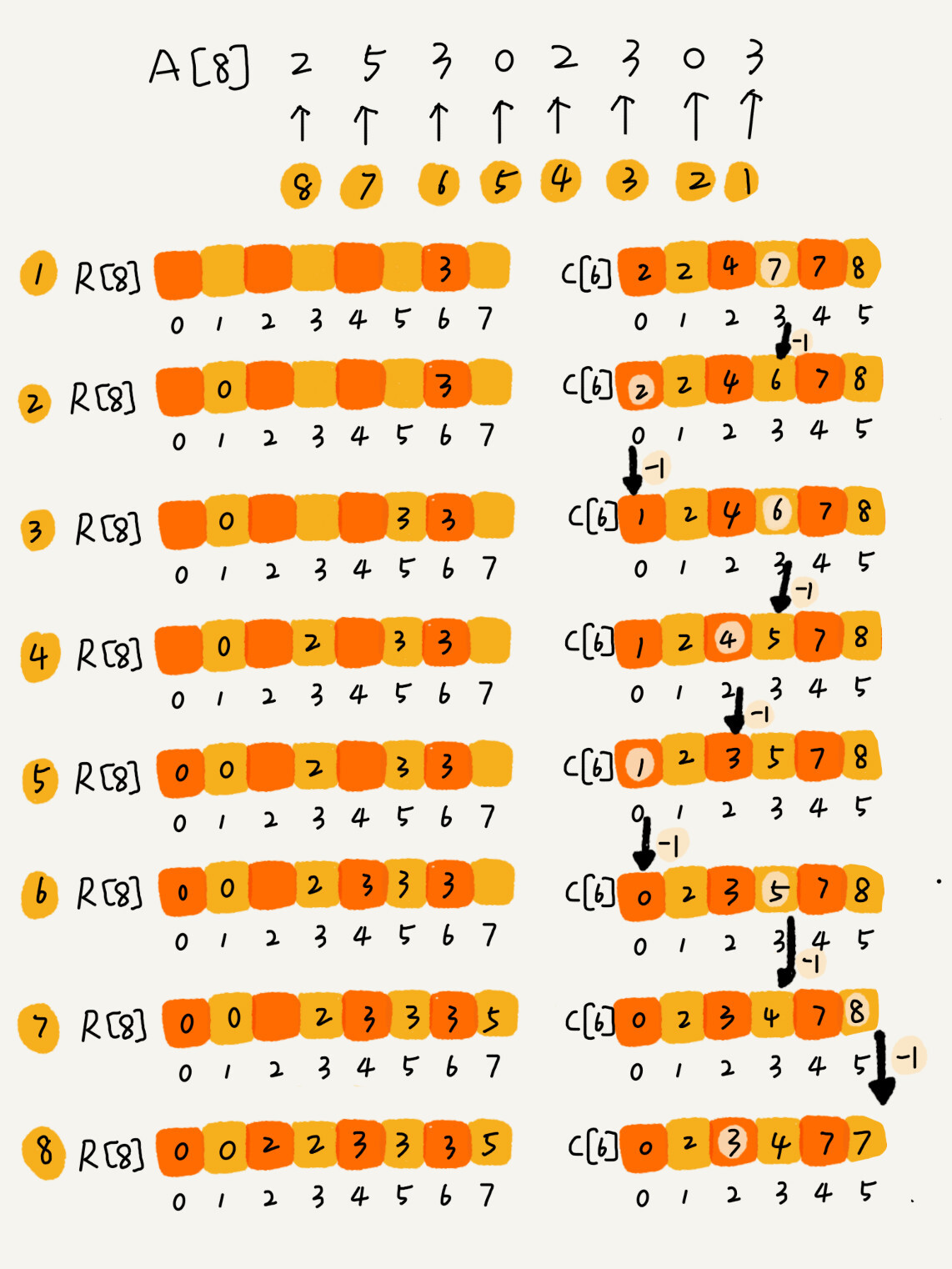
* 假设待排序的数组 `A = {2, 5, 3, 0, 2, 3, 0, 3}`,我们有计数数组 `C = {2, 0, 2, 3, 0, 1}`
|
||||
|
||||
接下来,我们要对 `C` 进行计数操作,具体来说,对从下标为 1 的元素开始累加 `C[i] += C[i - 1]`。
|
||||
|
||||
* 计数累加 `C = {2, 2, 4, 7, 7, 8}`
|
||||
|
||||
此时,`C` 中的元素表示「小于等于下标的元素的个数」。接下来,我们从尾至头扫描待排序数组 `A`,将其中元素依次拷贝到输出数组 `R` 的相应位置。我们注意到,`A[7] = 3` 而 `C[3] == 4` 。这意味着,待排序的数组中,包括 3 本身在内,不超过 3 的元素共有 4 个。因此,我们可以将这个 3 放置在 `R[C[3] - 1]` 的位置,而后将 `C[3]` 的计数减一——这是由于待排序数组中未处理的部分,不超过 3 的元素现在只剩下 3 个了。如此遍历整个待排序数组 `A`,即可得到排序后的结果 `R`。
|
||||
|
||||
|
||||
|
||||
### 算法分析
|
||||
|
||||
* 时间复杂度
|
||||
* $n$ 个元素,最大值是 $k$,分 $k$ 个「桶」;时间复杂度 $O(n)$
|
||||
* 桶内计数累加;时间复杂度 $O(k)$
|
||||
* 摆放元素;时间复杂度 $O(n)$
|
||||
* 当 $k < n$ 时,总体时间复杂度是 $O(n)$
|
||||
* 使用条件
|
||||
* $k < n$
|
||||
* 待排序数据的 key 是非负整数
|
||||
|
||||
## 基数排序(Radix Sort)
|
||||
|
||||
基数排序适用于等长数据的排序。对于不等长数据,可以在较短的数据后面做 padding,使得数据等长。
|
||||
|
||||
* 先就 least significant digit 进行稳定排序——通常可以用桶排序或者计数排序;时间复杂度 $O(n)$
|
||||
* 而后依次向 greatest significant digit 移动,进行稳定排序
|
||||
|
||||
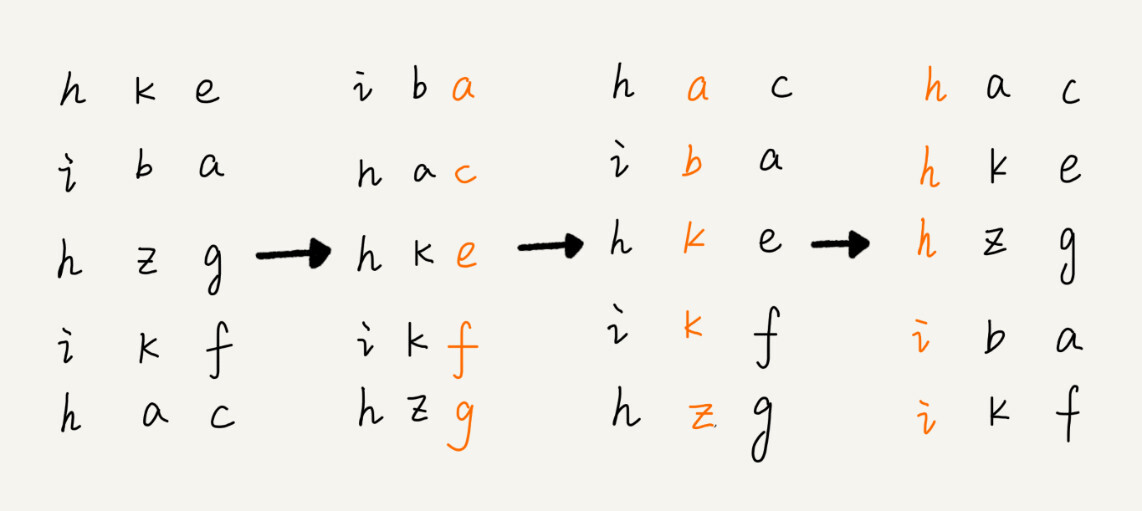
|
||||
|
||||
### 算法分析
|
||||
|
||||
* 时间复杂度
|
||||
* 对每一位的排序时间复杂度是 $O(n)$
|
||||
* 总共 $k$ 位,因此总的时间复杂度是 $O(kn)$;考虑到 $k$ 是常数,因此总的时间复杂度是 $O(n)$
|
||||
* 使用条件
|
||||
* 等长数据
|
||||
|
||||
## 解答开篇
|
||||
|
||||
桶排序。
|
||||
0
notes/14_sorts/.gitkeep
Normal file
0
notes/14_sorts/.gitkeep
Normal file
10
notes/14_sorts/readme.md
Normal file
10
notes/14_sorts/readme.md
Normal file
@ -0,0 +1,10 @@
|
||||
# 排序优化
|
||||
|
||||
## 如何取舍排序算法?
|
||||
|
||||
* 排序规模小 —— $O(n^2)$ 的算法(通常是插排)
|
||||
* 排序规模大 —— $O(n\log n)$ 的算法(通常不用归并排序)
|
||||
|
||||
## 如何优化快速排序?
|
||||
|
||||
参考:[谈谈内省式排序算法](https://liam.page/2018/08/29/introspective-sort/)
|
||||
0
notes/15_bsearch/.gitkeep
Normal file
0
notes/15_bsearch/.gitkeep
Normal file
23
notes/15_bsearch/readme.md
Normal file
23
notes/15_bsearch/readme.md
Normal file
@ -0,0 +1,23 @@
|
||||
# 二分查找(上)
|
||||
|
||||
## 算法描述
|
||||
|
||||
二分查找(Binary Search)也叫折半查找,是针对有序数据集合的查找算法。其描述十分简单:
|
||||
|
||||
* 折半取中,判断元素与目标元素的大小关系
|
||||
* 小于——往前继续折半
|
||||
* 大于——往后继续折半
|
||||
* 等于——返回
|
||||
|
||||
关于它的复杂度分析,参见[谈谈基于比较的排序算法的复杂度下界](https://liam.page/2018/08/28/lower-bound-of-comparation-based-sort-algorithm/)中的相关信息。它的复杂度是 $O(\log n)$。
|
||||
|
||||
## $O(\log n)$ 的惊人之处
|
||||
|
||||
在 42 亿个数据中用二分查找一个数据,最多需要比较 32 次。
|
||||
|
||||
## 适用场景
|
||||
|
||||
* 依赖顺序表结构
|
||||
* 数据本身必须有序
|
||||
* 数据量相对比较元素的开销要足够大——不然遍历即可
|
||||
* 数据量相对内存空间不能太大——不然顺序表装不下
|
||||
0
notes/16_bsearch/.gitkeep
Normal file
0
notes/16_bsearch/.gitkeep
Normal file
100
notes/16_bsearch/readme.md
Normal file
100
notes/16_bsearch/readme.md
Normal file
@ -0,0 +1,100 @@
|
||||
# 二分查找(下)
|
||||
|
||||
本节课讨论二分的各种变体。实际上在针对上一节的代码中,已经实现了两个变体。本次实现四个变体:
|
||||
|
||||
* 第一个等于给定值的元素
|
||||
* 最后一个等于给定值的元素
|
||||
* 第一个不小于给定值的元素
|
||||
* 最后一个不大于给定值的元素
|
||||
|
||||
```cpp
|
||||
/**
|
||||
* Created by Liam Huang (Liam0205) on 2018/10/26.
|
||||
*/
|
||||
|
||||
#ifndef BSEARCH_BSEARCH_VARIENTS_HPP_
|
||||
#define BSEARCH_BSEARCH_VARIENTS_HPP_
|
||||
|
||||
#include <iterator>
|
||||
#include <functional>
|
||||
|
||||
enum class BsearchPolicy { UNSPECIFIED, FIRST, LAST, FIRST_NOT_LESS, LAST_NOT_GREATER };
|
||||
|
||||
// Liam Huang: The algorithm works right with iterators that meet the ForwardIterator requirement,
|
||||
// but with a bad time complexity. For better performance, iterators should meet
|
||||
// the RandomAccessIterator requirement.
|
||||
template <typename IterT,
|
||||
typename ValueT = typename std::iterator_traits<IterT>::value_type,
|
||||
typename Compare>
|
||||
IterT bsearch(IterT first,
|
||||
IterT last,
|
||||
ValueT target,
|
||||
Compare comp,
|
||||
BsearchPolicy policy = BsearchPolicy::UNSPECIFIED) {
|
||||
IterT result = last;
|
||||
while (std::distance(first, last) > 0) {
|
||||
IterT mid = first + std::distance(first, last) / 2;
|
||||
if (policy == BsearchPolicy::FIRST_NOT_LESS) {
|
||||
if (!comp(*mid, target)) {
|
||||
if (mid == first or comp(*(mid - 1), target)) {
|
||||
result = mid;
|
||||
break;
|
||||
} else {
|
||||
last = mid;
|
||||
}
|
||||
} else {
|
||||
first = mid + 1;
|
||||
}
|
||||
} else if (policy == BsearchPolicy::LAST_NOT_GREATER) {
|
||||
if (comp(target, *mid)) {
|
||||
last = mid;
|
||||
} else {
|
||||
if (std::distance(mid, last) == 1 or comp(target, *(mid + 1))) {
|
||||
result = mid;
|
||||
break;
|
||||
} else {
|
||||
first = mid + 1;
|
||||
}
|
||||
}
|
||||
} else { // policy == UNSPECIFIED or FIRST or LAST
|
||||
if (comp(*mid, target)) {
|
||||
first = mid + 1;
|
||||
} else if (comp(target, *mid)) {
|
||||
last = mid;
|
||||
} else { // equal
|
||||
if (policy == BsearchPolicy::FIRST) {
|
||||
if (mid == first or comp(*(mid - 1), *mid)) {
|
||||
result = mid;
|
||||
break;
|
||||
} else {
|
||||
last = mid;
|
||||
}
|
||||
} else if (policy == BsearchPolicy::LAST) {
|
||||
if (std::distance(mid, last) == 1 or comp(*mid, *(mid + 1))) {
|
||||
result = mid;
|
||||
break;
|
||||
} else {
|
||||
first = mid + 1;
|
||||
}
|
||||
} else {
|
||||
result = mid;
|
||||
break;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
|
||||
template <typename IterT,
|
||||
typename ValueT = typename std::iterator_traits<IterT>::value_type,
|
||||
typename Compare = std::less<ValueT>>
|
||||
IterT bsearch(IterT first,
|
||||
IterT last,
|
||||
ValueT target,
|
||||
BsearchPolicy policy = BsearchPolicy::UNSPECIFIED) {
|
||||
return bsearch(first, last, target, Compare(), policy);
|
||||
}
|
||||
|
||||
#endif // BSEARCH_BSEARCH_VARIENTS_HPP_
|
||||
```
|
||||
0
notes/17_skiplist/.gitkeep
Normal file
0
notes/17_skiplist/.gitkeep
Normal file
43
notes/17_skiplist/readme.md
Normal file
43
notes/17_skiplist/readme.md
Normal file
@ -0,0 +1,43 @@
|
||||
# 跳表(Skip List)
|
||||
|
||||
支持快速地:
|
||||
|
||||
* 插入
|
||||
* 删除
|
||||
* 查找
|
||||
|
||||
某些情况下,跳表甚至可以替代红黑树(Red-Black tree)。Redis 当中的有序集合(Sorted Set)是用跳表实现的。
|
||||
|
||||
## 跳表的结构
|
||||
|
||||
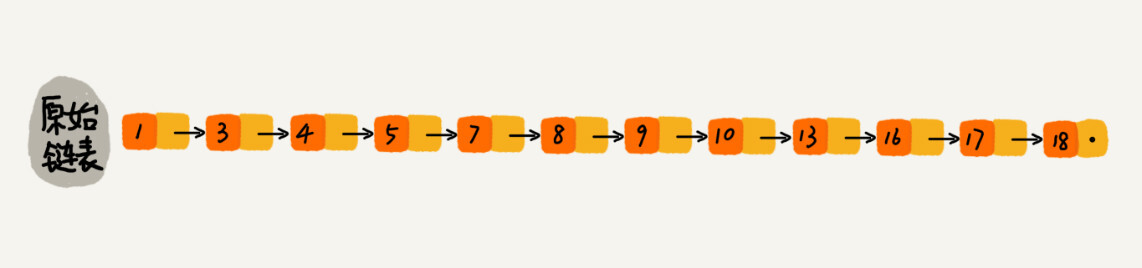
跳表是对链表的改进。对于单链表来说,即使内容是有序的,查找具体某个元素的时间复杂度也要达到 $O(n)$。对于二分查找来说,由于链表不支持随机访问,根据 `first` 和 `last` 确定 `cut` 时,必须沿着链表依次迭代 `std::distance(first, last) / 2` 步;特别地,计算 `std::(first, last)` 本身,就必须沿着链表迭代才行。此时,二分查找的效率甚至退化到了 $O(n \log n)$,甚至还不如顺序遍历。
|
||||
|
||||
|
||||
|
||||
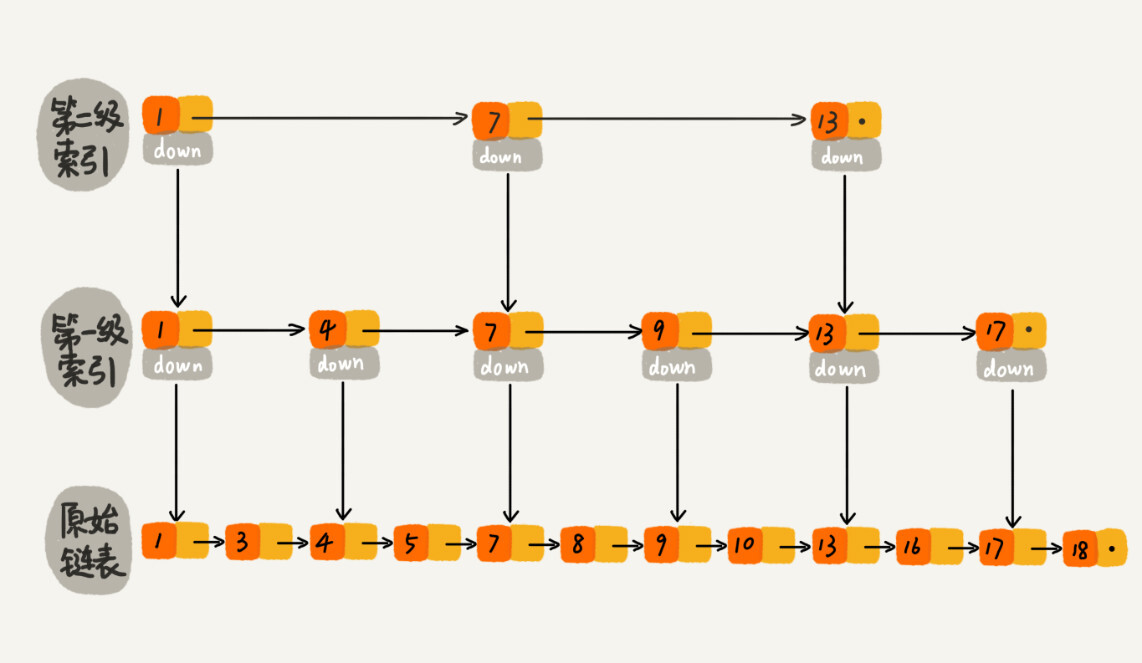
跳表的核心思想是用空间换时间,构建足够多级数的索引,来缩短查找具体值的时间开销。
|
||||
|
||||
|
||||
|
||||
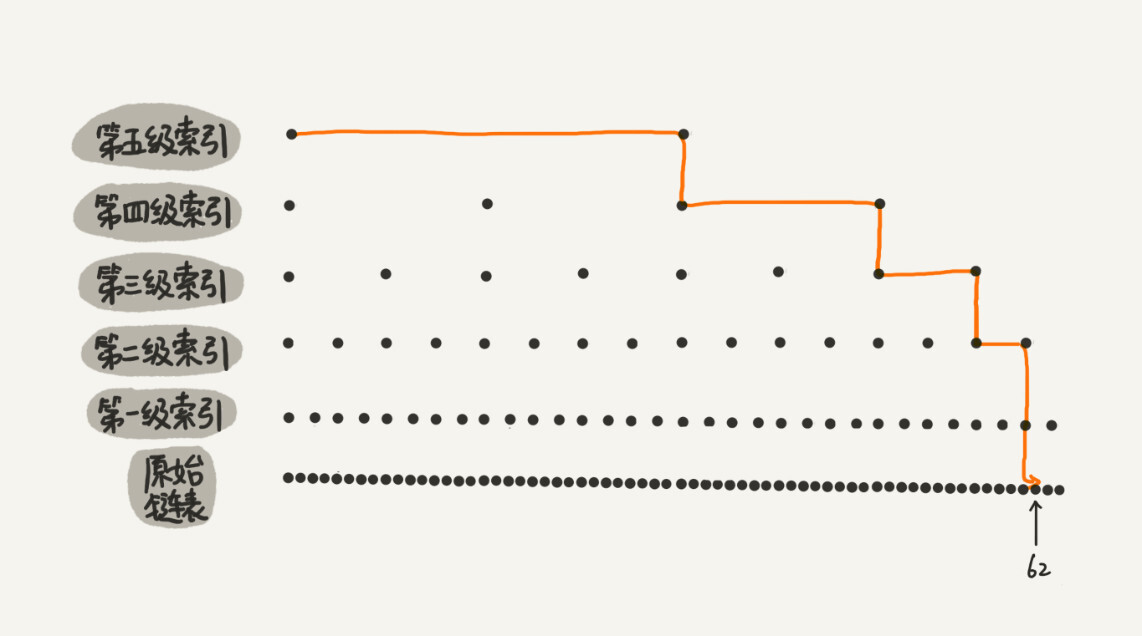
例如对于一个具有 64 个有序元素的五级跳表,查找起来的过程大约如下图所示。
|
||||
|
||||
|
||||
|
||||
## 复杂度分析
|
||||
|
||||
对于一个每一级索引的跨度是下一级索引 $k$ 倍的跳表,每一次 `down` 操作,相当于将搜索范围缩小到「剩余的可能性的 $1 / k$」。因此,查找具体某个元素的时间复杂度大约需要 $\lfloor \log_k n\rfloor + 1$ 次操作;也就是说时间复杂度是 $O(\log n)$。
|
||||
|
||||
|
||||
|
||||
前面说了,跳表是一种用空间换时间的数据结构。因此它的空间复杂度一定不小。我们考虑原链表有 $n$ 个元素,那么第一级索引就有 $n / k$ 个元素,剩余的索引依次有 $n / k^2$, $n / k^3$, ..., $1$ 个元素。总共的元素个数是一个等比数列求和问题,它的值是 $\frac{n - 1}{k - 1}$。可见,不论 $k$ 是多少,跳表的空间复杂度都是 $O(n)$;但随着 $k$ 的增加,实际需要的额外节点数会下降。
|
||||
|
||||
## 高效地插入和删除
|
||||
|
||||
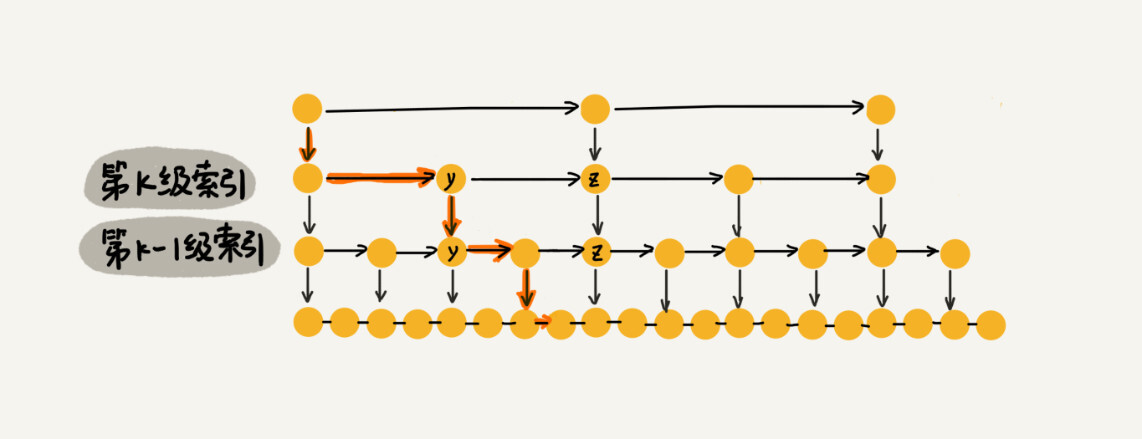
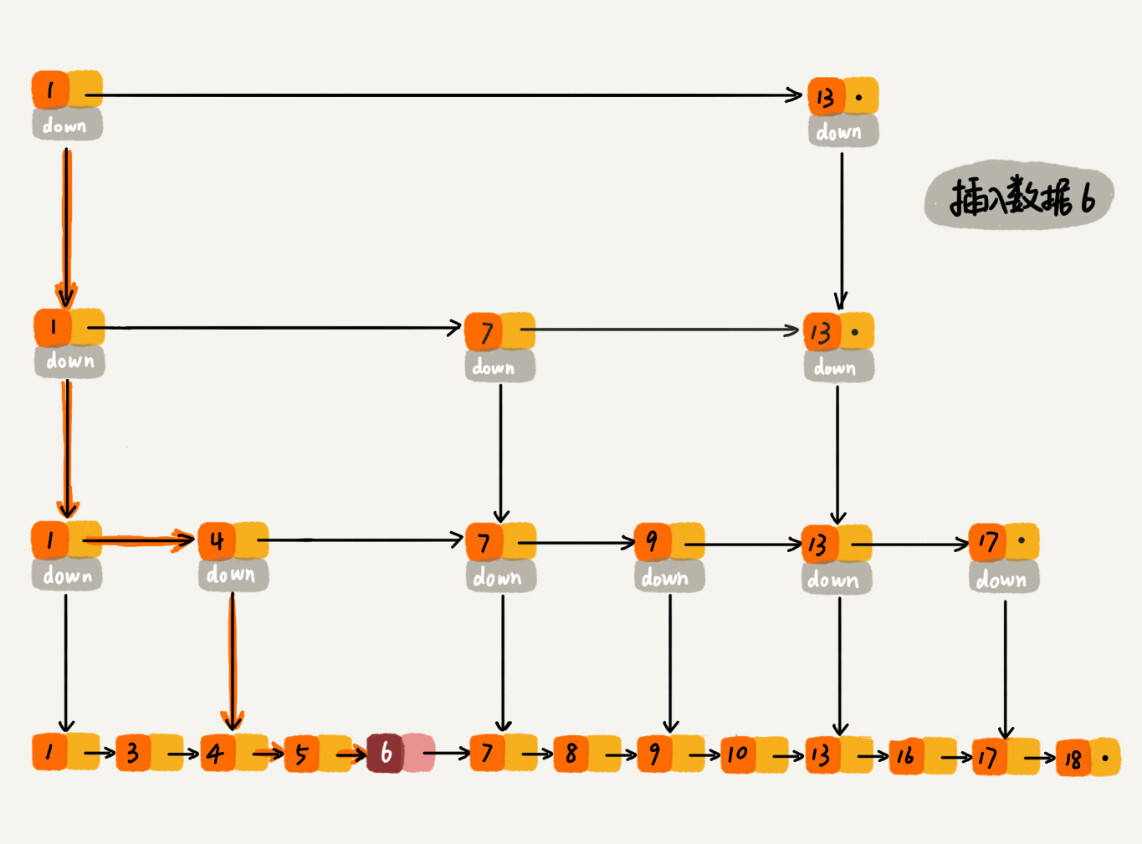
对于链表来说,插入或删除一个给定结点的时间复杂度是 $O(1)$。因此,对于跳表来说,插入或删除某个结点,其时间复杂度完全依赖于查找这类结点的耗时。而我们知道,在跳表中查找某个元素的时间复杂度是 $O(\log n)$。因此,在跳表中插入或删除某个结点的时间复杂度是 $O(\log n)$。
|
||||
|
||||
|
||||
|
||||
## 跳表索引的动态更新
|
||||
|
||||
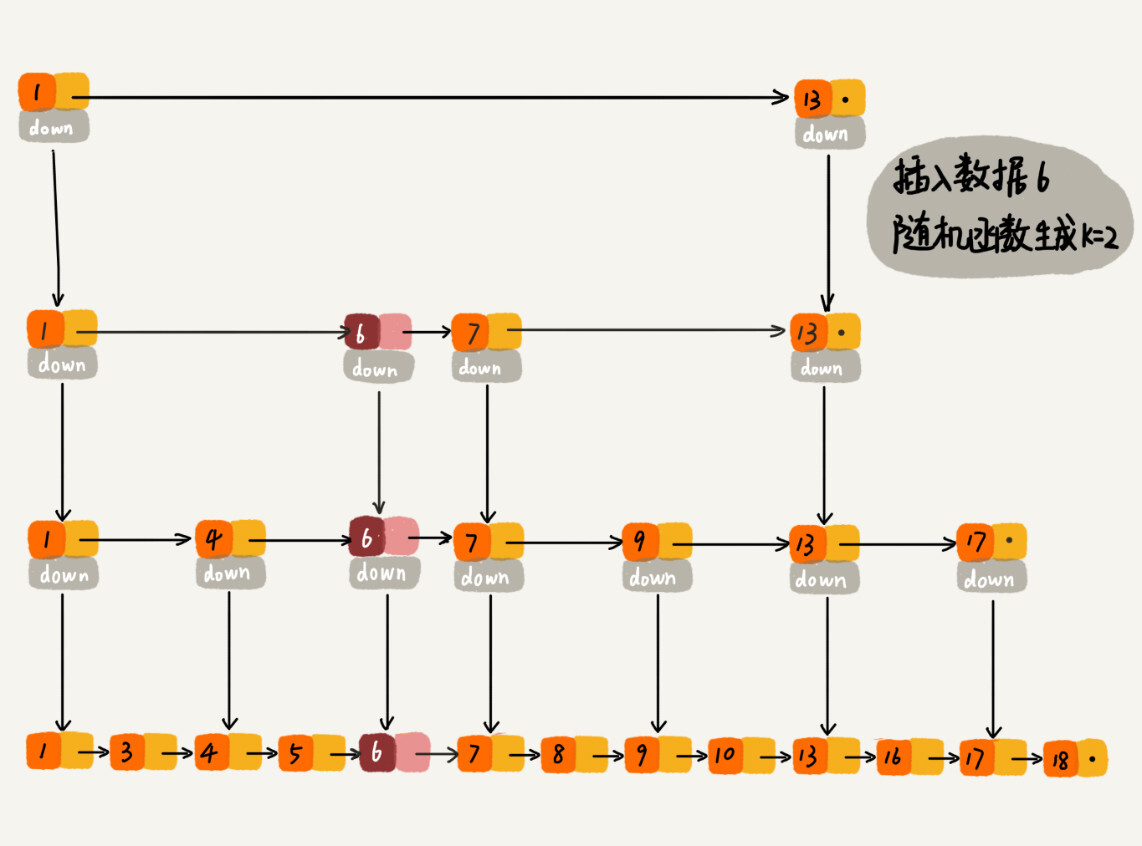
为了维护跳表的结构,在不断插入数据的过程中,有必要动态维护跳表的索引结构。一般来说,可以采用随机层级法。具体来说是引入一个输出整数的随机函数。当随机函数输出 $K$,则更新从第 $1$ 级至第 $K$ 级的索引。为了保证索引结构和数据规模大小的匹配,一般采用二项分布的随机函数。
|
||||
|
||||
|
||||
Loading…
Reference in New Issue
Block a user