新增文章
This commit is contained in:
zhuyijun
parent
6688c60959
commit
a24396bf30
@ -113,7 +113,7 @@ theme: butterfly
|
||||
## Docs: https://hexo.io/docs/one-command-deployment
|
||||
deploy:
|
||||
type: git
|
||||
repo: https://gogs.zyjblogs.cn/zhuyijun/hexo.zyjblogs.cn.git
|
||||
repo: git@gogs.zyjblogs.cn:zhuyijun/hexo.zyjblogs.cn.git
|
||||
branch: master
|
||||
|
||||
bangumi:
|
||||
|
||||
5793
package-lock.json
generated
Normal file
5793
package-lock.json
generated
Normal file
File diff suppressed because it is too large
Load Diff
@ -3,7 +3,7 @@
|
||||
"version": "0.0.0",
|
||||
"private": true,
|
||||
"scripts": {
|
||||
"build": "hexo generate",
|
||||
"build": "hexo clean && hexo bangumi -u && hexo generate",
|
||||
"clean": "hexo clean",
|
||||
"deploy": "hexo deploy",
|
||||
"server": "hexo server"
|
||||
|
||||
File diff suppressed because one or more lines are too long
156
source/_posts/algorithm/backtracking/nqueens/NQueens.md
Normal file
156
source/_posts/algorithm/backtracking/nqueens/NQueens.md
Normal file
@ -0,0 +1,156 @@
|
||||
---
|
||||
title: N皇后
|
||||
date: 2024-3-19
|
||||
tag:
|
||||
- 算法
|
||||
- 回溯
|
||||
- 递归
|
||||
categories: 算法
|
||||
abbrlink: bd497d25
|
||||
---
|
||||
|
||||
# N皇后
|
||||
[51. N皇后](https://leetcode-cn.com/problems/n-queens/)
|
||||
### 题目描述
|
||||
> n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
|
||||
>
|
||||
|
||||
>
|
||||
上图为 8 皇后问题的一种解法。
|
||||
>
|
||||
给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。
|
||||
>
|
||||
每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。
|
||||
|
||||
示例：
|
||||
|
||||
```
|
||||
输入: 4
|
||||
输出: [
|
||||
[".Q..", // 解法 1
|
||||
"...Q",
|
||||
"Q...",
|
||||
"..Q."],
|
||||
|
||||
["..Q.", // 解法 2
|
||||
"Q...",
|
||||
"...Q",
|
||||
".Q.."]
|
||||
]
|
||||
解释: 4 皇后问题存在两个不同的解法。
|
||||
```
|
||||
|
||||
### 问题分析
|
||||
约束条件为每个棋子所在的行、列、对角线都不能有另一个棋子。
|
||||
|
||||
使用一维数组表示一种解法，下标（index）表示行，值（value）表示该行的Q（皇后）在哪一列。
|
||||
每行只存储一个元素，然后递归到下一行，这样就不用判断行了，只需要判断列和对角线。
|
||||
### Solution1
|
||||
当result[row] = column时，即row行的棋子在column列。
|
||||
|
||||
对于[0, row-1]的任意一行（i 行），若 row 行的棋子和 i 行的棋子在同一列，则有result[i] == column;
|
||||
若 row 行的棋子和 i 行的棋子在同一对角线，等腰直角三角形两直角边相等，即 row - i == Math.abs(result[i] - column)
|
||||
|
||||
布尔类型变量 isValid 的作用是剪枝，减少不必要的递归。
|
||||
```java
|
||||
public List<List<String>> solveNQueens(int n) {
|
||||
// 下标代表行，值代表列。如result[0] = 3 表示第1行的Q在第3列
|
||||
int[] result = new int[n];
|
||||
List<List<String>> resultList = new LinkedList<>();
|
||||
dfs(resultList, result, 0, n);
|
||||
return resultList;
|
||||
}
|
||||
|
||||
void dfs(List<List<String>> resultList, int[] result, int row, int n) {
|
||||
// 递归终止条件
|
||||
if (row == n) {
|
||||
List<String> list = new LinkedList<>();
|
||||
for (int x = 0; x < n; ++x) {
|
||||
StringBuilder sb = new StringBuilder();
|
||||
for (int y = 0; y < n; ++y)
|
||||
sb.append(result[x] == y ? "Q" : ".");
|
||||
list.add(sb.toString());
|
||||
}
|
||||
resultList.add(list);
|
||||
return;
|
||||
}
|
||||
for (int column = 0; column < n; ++column) {
|
||||
boolean isValid = true;
|
||||
result[row] = column;
|
||||
/*
|
||||
* 逐行往下考察每一行。同列，result[i] == column
|
||||
* 同对角线，row - i == Math.abs(result[i] - column)
|
||||
*/
|
||||
for (int i = row - 1; i >= 0; --i) {
|
||||
if (result[i] == column || row - i == Math.abs(result[i] - column)) {
|
||||
isValid = false;
|
||||
break;
|
||||
}
|
||||
}
|
||||
if (isValid) dfs(resultList, result, row + 1, n);
|
||||
}
|
||||
}
|
||||
```
|
||||
### Solution2
|
||||
使用LinkedList表示一种解法，下标（index）表示行，值（value）表示该行的Q（皇后）在哪一列。
|
||||
|
||||
解法二和解法一的不同在于，相同列以及相同对角线的校验。
|
||||
将对角线抽象成【一次函数】这个简单的数学模型，根据一次函数的截距是常量这一特性进行校验。
|
||||
|
||||
这里，我将右上-左下对角线，简称为“\”对角线；左上-右下对角线简称为“/”对角线。
|
||||
|
||||
“/”对角线斜率为1，对应方程为y = x + b，其中b为截距。
|
||||
对于线上任意一点，均有y - x = b，即row - i = b;
|
||||
定义一个布尔类型数组anti_diag，将b作为下标，当anti_diag[b] = true时，表示相应对角线上已经放置棋子。
|
||||
但row - i有可能为负数，负数不能作为数组下标，row - i 的最小值为-n（当row = 0，i = n时），可以加上n作为数组下标，即将row -i + n 作为数组下标。
|
||||
row - i + n 的最大值为 2n（当row = n，i = 0时），故anti_diag的容量设置为 2n 即可。
|
||||
|
||||
|
||||
|
||||
“\”对角线斜率为-1，对应方程为y = -x + b，其中b为截距。
|
||||
对于线上任意一点，均有y + x = b，即row + i = b;
|
||||
同理，定义数组main_diag，将b作为下标，当main_diag[row + i] = true时，表示相应对角线上已经放置棋子。
|
||||
|
||||
有了两个校验对角线的数组，再来定义一个用于校验列的数组cols，这个太简单啦，不解释。
|
||||
|
||||
**解法二时间复杂度为O(n!)，在校验相同列和相同对角线时，引入三个布尔类型数组进行判断。相比解法一，少了一层循环，用空间换时间。**
|
||||
|
||||
```java
|
||||
List<List<String>> resultList = new LinkedList<>();
|
||||
|
||||
public List<List<String>> solveNQueens(int n) {
|
||||
boolean[] cols = new boolean[n];
|
||||
boolean[] main_diag = new boolean[2 * n];
|
||||
boolean[] anti_diag = new boolean[2 * n];
|
||||
LinkedList<Integer> result = new LinkedList<>();
|
||||
dfs(result, 0, cols, main_diag, anti_diag, n);
|
||||
return resultList;
|
||||
}
|
||||
|
||||
void dfs(LinkedList<Integer> result, int row, boolean[] cols, boolean[] main_diag, boolean[] anti_diag, int n) {
|
||||
if (row == n) {
|
||||
List<String> list = new LinkedList<>();
|
||||
for (int x = 0; x < n; ++x) {
|
||||
StringBuilder sb = new StringBuilder();
|
||||
for (int y = 0; y < n; ++y)
|
||||
sb.append(result.get(x) == y ? "Q" : ".");
|
||||
list.add(sb.toString());
|
||||
}
|
||||
resultList.add(list);
|
||||
return;
|
||||
}
|
||||
for (int i = 0; i < n; ++i) {
|
||||
if (cols[i] || main_diag[row + i] || anti_diag[row - i + n])
|
||||
continue;
|
||||
result.add(i);
|
||||
cols[i] = true;
|
||||
main_diag[row + i] = true;
|
||||
anti_diag[row - i + n] = true;
|
||||
dfs(result, row + 1, cols, main_diag, anti_diag, n);
|
||||
result.removeLast();
|
||||
cols[i] = false;
|
||||
main_diag[row + i] = false;
|
||||
anti_diag[row - i + n] = false;
|
||||
}
|
||||
}
|
||||
```
|
||||
88
source/_posts/algorithm/dp/ways/状态转移方程.md
Normal file
88
source/_posts/algorithm/dp/ways/状态转移方程.md
Normal file
@ -0,0 +1,88 @@
|
||||
---
|
||||
title: 状态转移方程
|
||||
date: 2024-3-19
|
||||
tag:
|
||||
- dp
|
||||
categories:
|
||||
- 算法
|
||||
abbrlink: 92fa7813
|
||||
---
|
||||
|
||||
# 状态转移方程
|
||||
|
||||
## **定义**
|
||||
|
||||
[动态规划](https://baike.so.com/doc/6995222-7218096.html)中本阶段的状态往往是上一阶段状态和上一阶段决策的结果。若给定了第K阶段的状态Sk以及决策uk(Sk),则第K+1阶段的状态Sk+1也就完全确定。也就是说Sk+1与Sk,uk之间存在一种明确的数量对应关系，记为Tk(Sk,uk),即有Sk+1= Tk(Sk,uk)。 这种用函数表示前后阶段关系的方程，称为状态转移方程。在上例中状态转移方程为 Sk+1= uk(Sk) 。
|
||||
|
||||
## **设计**
|
||||
|
||||
适用条件
|
||||
|
||||
任何思想方法都有一定的局限性，超出了特定条件，它就失去了作用。同样，动态规划也并不是万能的。适用动态规划的问题必须满足最优化原理和无后效性。
|
||||
|
||||
1.[最优化原理](https://baike.so.com/doc/1852557-1959037.html)(最优子结构性质) 最优化原理可这样阐述:一个最优化策略具有这样的性质，不论过去状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。简而言之，一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
|
||||
|
||||
2.无后效性将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。
|
||||
|
||||
3.子问题的重叠性 动态规划将原来具有指数级时间复杂度的[搜索算法](https://baike.so.com/doc/6058609-6271658.html)改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余，这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术，它在实现的过程中，不得不存储产生过程中的各种状态，所以它的空间复杂度要大于其它的算法。
|
||||
|
||||
如何设计动态转移方程
|
||||
|
||||
如果满足上述条件，一般可以按照以下步骤进行设计:
|
||||
|
||||
一、确定问题的[决策对象](https://baike.so.com/doc/8780581-9104627.html)
|
||||
|
||||
二、对决策对象划分阶段
|
||||
|
||||
三、对各阶段确定[状态变量](https://baike.so.com/doc/1032672-1092144.html)
|
||||
|
||||
四、根据状态变量确定费用函数和目标函数
|
||||
|
||||
五、建立各阶段的状态变量的转移方程，写出状态转移方程
|
||||
|
||||
六、编程实现
|
||||
|
||||
## **状态转移方程的代码实现**
|
||||
|
||||
假设列出了状态转移方程:d(i, j) = a(i, j) + max{d(i + 1, j), d(i + 1, j + 1)}。
|
||||
|
||||
### [折叠](https://baike.so.com/doc/2649061-2797348.html#)**递归计算**
|
||||
|
||||
```cpp
|
||||
int d(int i, int j){
|
||||
return a[i][j] + (i == n ? 0 : (d(i + 1, j) > d(i + 1, j + 1) ? d(i + 1, j) : d(i + 1, j + 1)));
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
递归方法的缺点是:效率比较低，首先在调用函数的嵌套时，函数不断的切换，由此降低了效率。其次是相同的子问题被重复求解，例如:d(2, 3), d(4, 2), d(4, 3)就是被重复求解了两次。
|
||||
|
||||
### [折叠](https://baike.so.com/doc/2649061-2797348.html#)**递推计算**
|
||||
|
||||
```cpp
|
||||
int i, j;
|
||||
for(j = 1; j <= n; ++j)
|
||||
d[n][j] = a[n][j];
|
||||
for(i = n-1; i >= 1; --i)
|
||||
for(j = 1; j <= i; ++j)
|
||||
d[i][j] = a[i][j] + (d[i + 1][j] > d[i + 1][j + 1] ? d[i + 1][j] : d[i + 1][j + 1]);
|
||||
```
|
||||
|
||||
递推要注意边界的处理。
|
||||
|
||||
### [折叠](https://baike.so.com/doc/2649061-2797348.html#)**记忆化搜索**
|
||||
|
||||
首先设置一个数组，目的是保存已经计算好的子问题的解，下次再计算相同子问题时，就不用重复求解了，如下设置一个st数组用来保存计算好的子问题的解，初始化st所有元素为-1。
|
||||
|
||||
```cpp
|
||||
int d(int i, int j){
|
||||
if(st[i][j] > 0)
|
||||
return st[i][j];
|
||||
return st[i][j] = a[i][j] + (i == n ? 0 : (d(i + 1, j) > d(i + 1, j + 1) ? d(i + 1, j) : d(i + 1, j + 1)));
|
||||
}
|
||||
```
|
||||
|
||||
记忆化搜索用的也是递归的方法，目的是把子问题的解保存下来，避免重复计算的情况，这是它比纯递归更高效的原因。
|
||||
|
||||
记忆化搜索跟递推相比，它的优点是:它不必事先确定好各状态的计算顺序，但使用递推时必须事先确定好计算顺序。
|
||||
269
source/_posts/algorithm/graph/serach/寻路算法之AStar算法原理及实现.md
Normal file
269
source/_posts/algorithm/graph/serach/寻路算法之AStar算法原理及实现.md
Normal file
@ -0,0 +1,269 @@
|
||||
---
|
||||
title: 「游戏」寻路算法之A Star算法原理及实现
|
||||
date: 2024-3-19
|
||||
tag:
|
||||
- 图
|
||||
categories: 算法
|
||||
abbrlink: '0'
|
||||
---
|
||||
## 「游戏」寻路算法之A Star算法原理及实现
|
||||
|
||||
## 前言
|
||||
|
||||
自动寻路是在一些如MMORPG等类型游戏中常见的一种功能，其给了玩家良好的游戏体验，使得玩家在游戏过程中省去了大量游戏坐标点的记录以及长时间的键盘操作，不必记忆坐标，不必担心迷路，用最快捷的方法移动到指定地点。
|
||||
|
||||
寻路算法（自动寻路算法，下同），其实可以看作是一种路径查找算法以及图搜索算法，图搜索（Graph Search）算法是用于在图上进行一般性发现或显式地搜索的算法。这些算法在图上找到出路径，但没有期望这些路径是在计算意义上是最优的。
|
||||
|
||||
路径查找算法（Pathfinding）是建立在图搜索算法的基础上，它探索节点之间的路径，从一个节点开始，遍历关系，直到到达目的节点。这些算法用于识别图中的最优路由，算法可以用于诸如物流规划、最低成本呼叫或IP路由以及游戏模拟等用途。
|
||||
|
||||
常见的路径搜索算法和图搜索算法有：A*（A Star）算法、Dijkstra算法、广（深）度优先搜索、最佳优先搜索、Jump Point Search算法等，今天本文主要讲解的是A*（A Star）算法的原理以及实现。
|
||||
|
||||
## 常见搜索算法
|
||||
|
||||
### Dijkstra算法
|
||||
|
||||
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止[^1]。
|
||||
|
||||
在游戏中（仅以2D为例），我们把某个场景的地图按照一定的规则划分成一个个的小格子，每个格子代表一个可用的坐标点，该坐标点有两种状态分别为：有效、无效。其中有效状态代表为该坐标点玩家可以正常通过，无效为该坐标点玩家无法到达，即当前坐标点可能存在阻挡物，如河流、山川、npc等，并且，以每个格子（以正方形为例）为中心可以分别向8个不同方向前进，在像每个方向前进时，所需的代价是不同的。
|
||||
|
||||
> 举个例子（后续的所有移动代价皆以此计算）
|
||||
>
|
||||
> 当玩家向自身8个方向中的横轴以及纵轴进行移动时（即向上、下、左、右），移动代价为10（别问为啥为10，拍脑门决定的）。
|
||||
>
|
||||
> 当玩家向自身八个方向中的对角方向进行移动时（即左上、左下、右上、右下），移动代价为横（纵）轴移动的1.4倍（因为正方形的对角线是边长约1.4倍）。
|
||||
|
||||
在使用该算法的时候需要选择一个周围8方向中，距离起点总移动代价最低的节点作为下一个要遍历的节点，一直到当前节点为终点或者无可用节点为止。那么此时就需要一个优先队列来保存当前节点的8方向中的可用节点、以方便的查找到移动代价最低的节点。
|
||||
|
||||
|
||||
|
||||
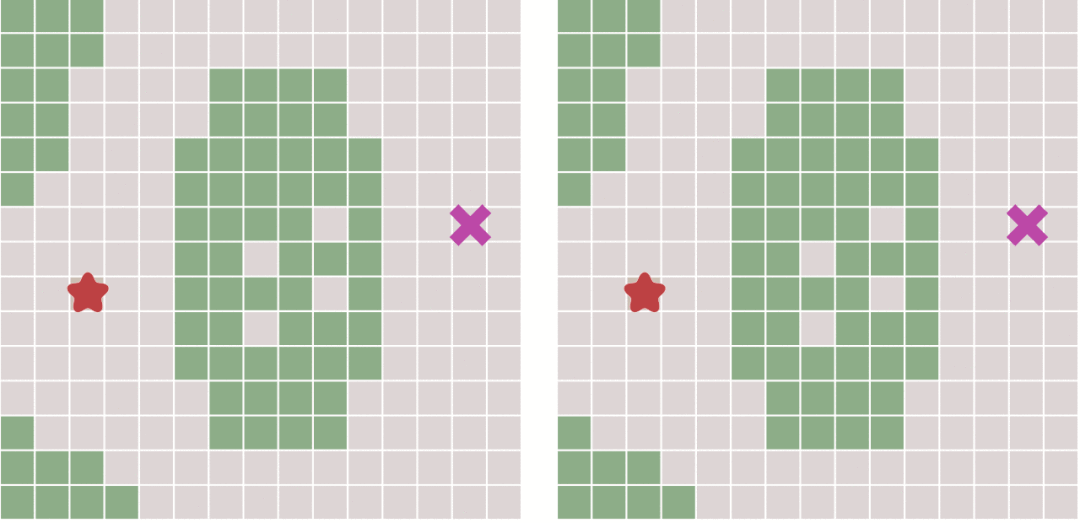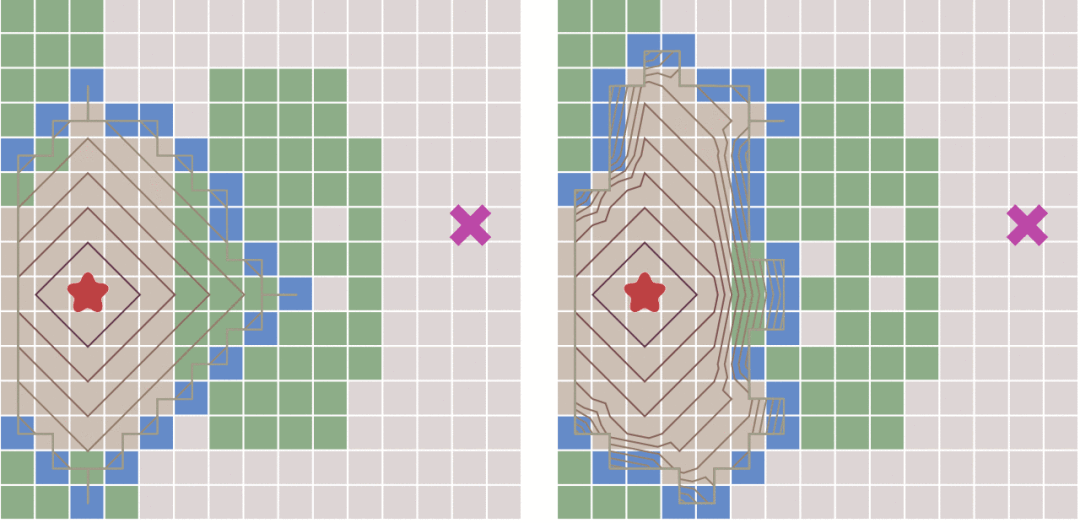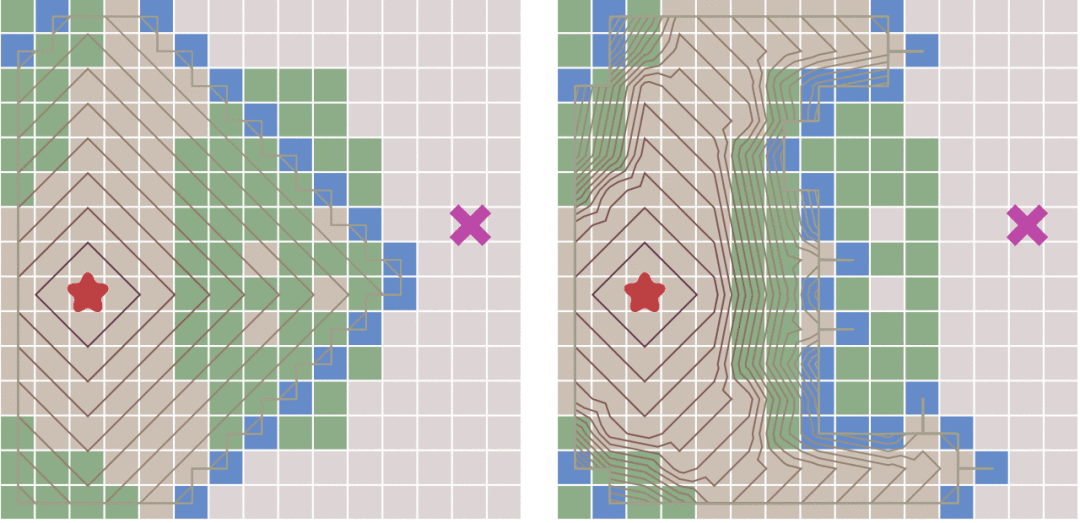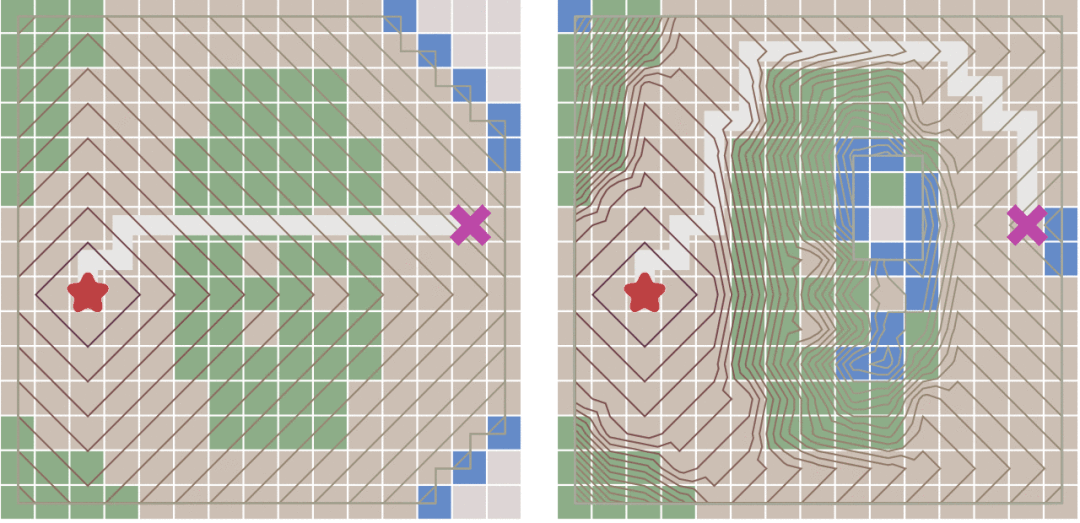
> 左图为BFS算法右图为Dijkstra算法（图侵删）
|
||||
>
|
||||
> 上图对比了不考虑节点移动代价差异的广度优先搜索与考虑移动代价的Dijkstra算法的运行图
|
||||
|
||||
应当注意，绝大多数的戴克斯特拉算法不能有效处理移动代价为负的图[^2]。
|
||||
|
||||
### 最佳优先搜索算法（Best-First-Search）
|
||||
|
||||
最佳优先搜索算法是一种启发式搜索算法（Heuristic Algorithm），其基于广度优先搜索算法，不同点是其依赖于估价函数对将要遍历的节点进行估价，选择代价小的节点进行遍历，直到找到目标点为止。BFS算法不能保证找到的路径是一条最短路径，但是其计算过程相对于Dijkstra算法会快很多[^3]。
|
||||
|
||||
所谓的启发式搜索算法，就是针对游戏地图中的每一个位置节点进行评估，从而得到相对来说最优的位置，而后再从这个最优为止再次进行搜索，直到符合终止条件或者超出地图范围为止，这样可以省略大量无谓的搜索路径，提高了效率。在启发式搜索中，对位置的预估是十分重要的。因此就需要使用启发函数来进行位置预估。
|
||||
|
||||
这个算法和Dijkstra算法差不多，同样也使用一个优先队列，但此时以每个节点的移动代价作为优先级去比较，每次都选取移动代价最小的，因为此时距离终点越来越近，所以说这种算法称之为最佳优先（Best First）算法。
|
||||
|
||||
接下来看一下运行事例：
|
||||
|
||||
|
||||
|
||||
> 图侵删
|
||||
>
|
||||
> 左侧为Dijkstra算法右侧为最佳优先搜索算法
|
||||
|
||||
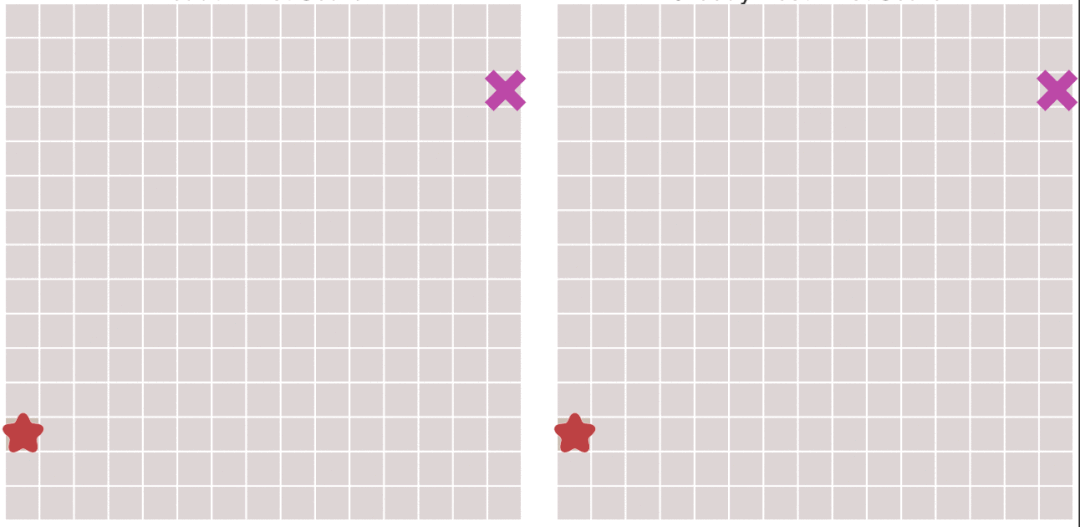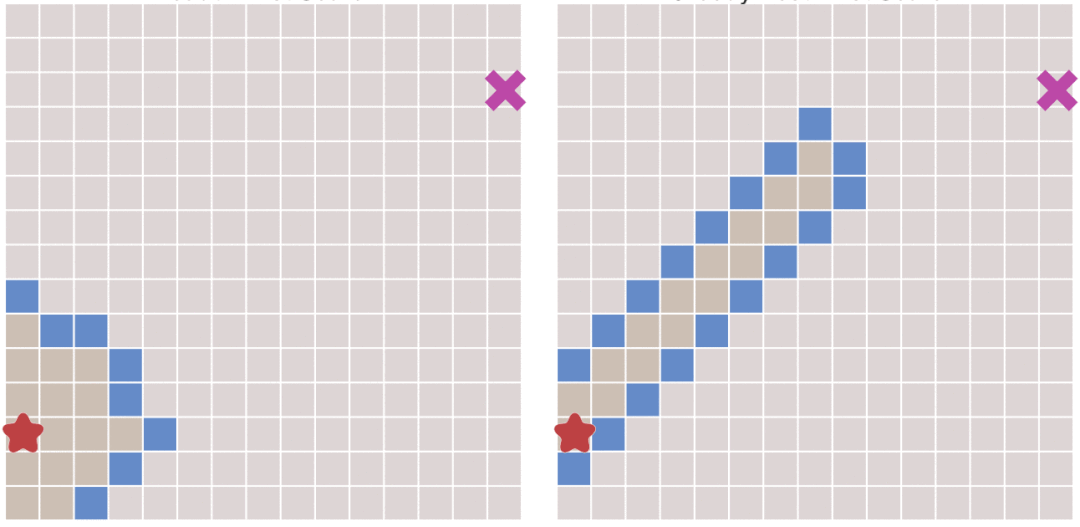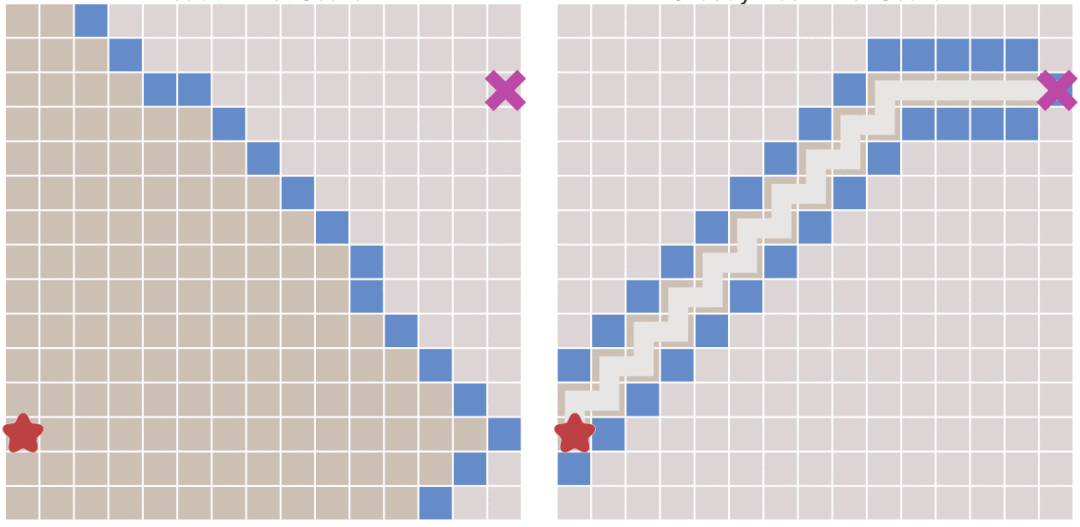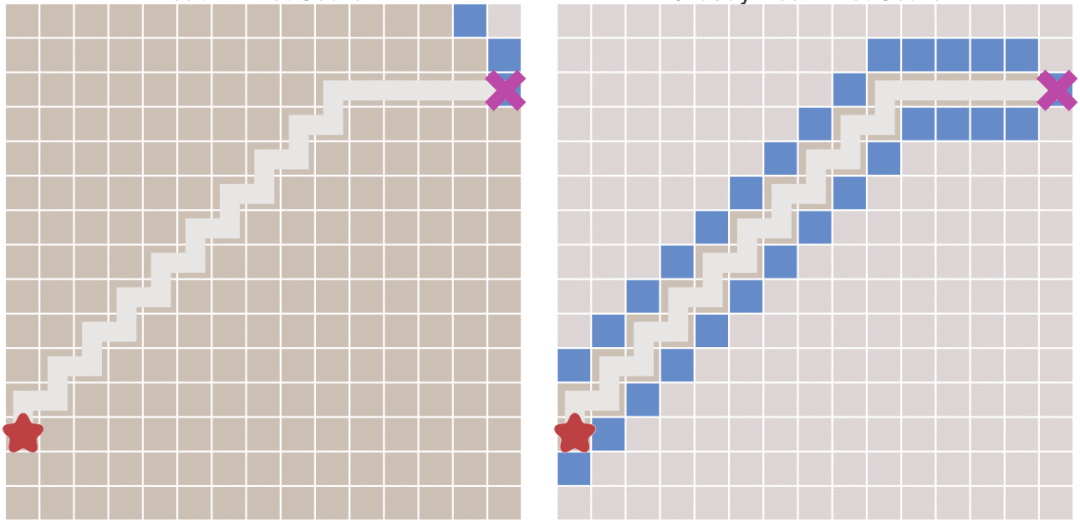
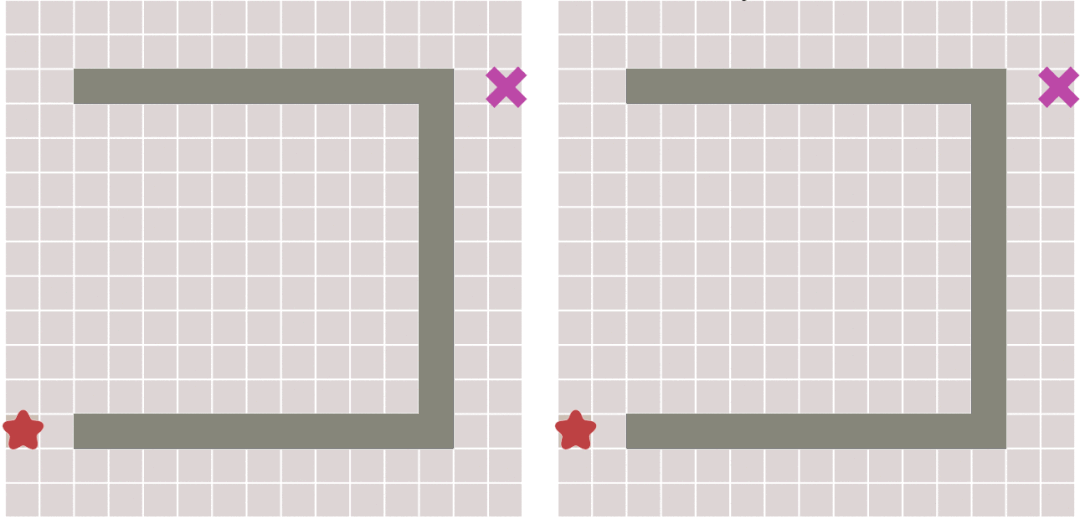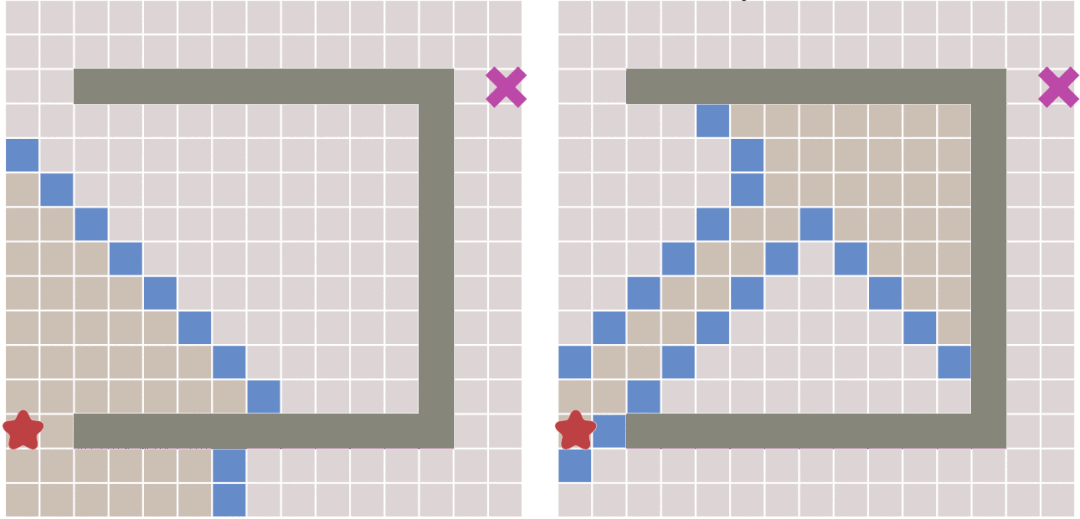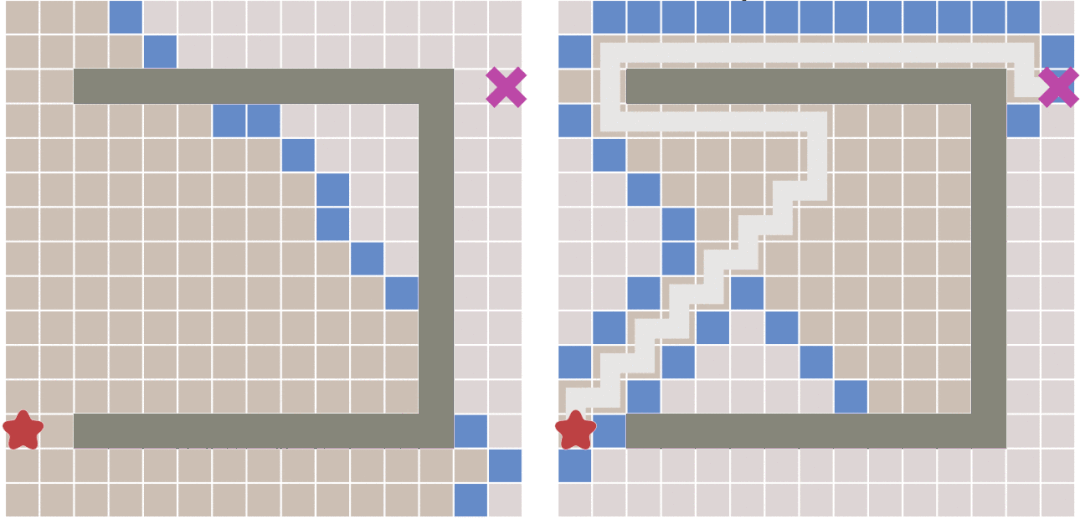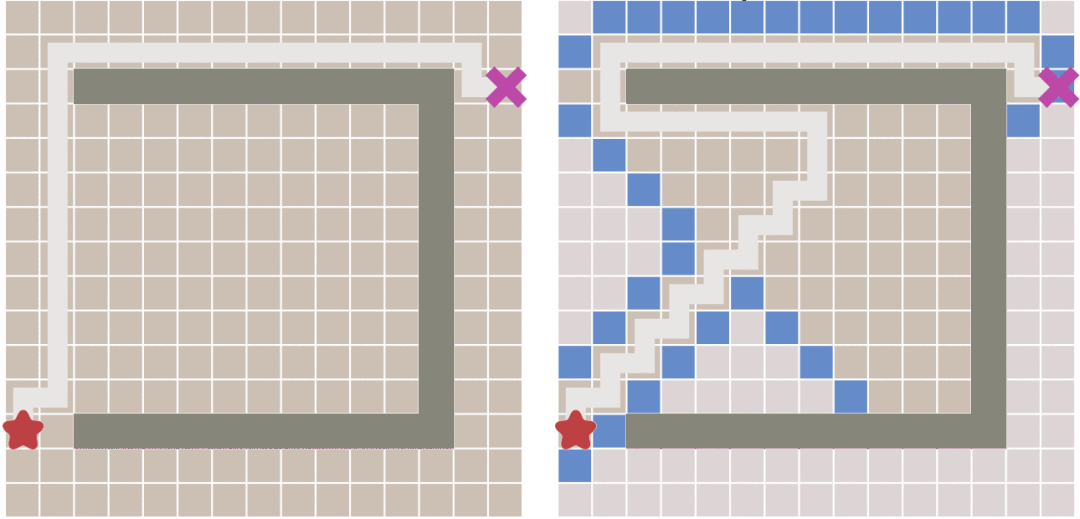
最佳优先搜索算法相对于Dijkstra算法的问题在哪里呢？看一下中途有阻挡的时候的情况：
|
||||
|
||||
|
||||
|
||||
> 图侵删
|
||||
>
|
||||
> 左侧为Dijkstra算法右侧为最佳优先搜索算法
|
||||
|
||||
从上图中可以看出，当地图中存在障碍物的时候，最佳优先搜索算法并不能找到最短路径。
|
||||
|
||||
### A Star 算法
|
||||
|
||||
A Star算法是一种在游戏开发过程中很常用的自动寻路算法。它有较好的性能和准确度。**A\*搜索算法**（A* search algorithm）是一种在图形平面上，有多个节点的路径，求出最低通过成本的算法。常用于游戏中的NPC的移动计算，或网络游戏的BOT的移动计算上。该算法综合了最佳优先搜索和Dijkstra算法的优点：在进行启发式搜索提高算法效率的同时，可以保证找到一条基于启发函数的最优路径[^4]。
|
||||
|
||||
### 启发公式
|
||||
|
||||
A Star算法也是一种启发式搜索算法那么其与最佳优先搜索算法一样需要一个启发函数左右计算移动代价的方法，那么A Star的启发函数公式为：$$ f(n) = g(n)+h(n) $$
|
||||
|
||||
解释下这个公式的各项的含义：
|
||||
|
||||
•**h(n)**:从当前节点n到终点的预估的代价。•**g(n)**:从起始点到达当前节点n的代价。•**f(n)**:为当前节点n的综合的代价，在选择下一个节点的时候，其值越低，优先级就越高（因为代价小）。
|
||||
|
||||
关于启发函数中*h(n)**公式的的选择，由于游戏地图中大部分都是被分为网格形式（即整个地图被拆分为多个正方形格子），那么此时就有3种可选的启发函数的**h(n)*公式可用，分别为：
|
||||
|
||||
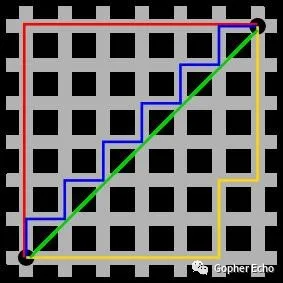
> 曼哈顿距离：出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。
|
||||
>
|
||||
> 
|
||||
>
|
||||
> 曼哈顿距离一般用在在移动时，只允许朝上下左右四个方向移动的情况下使用。
|
||||
>
|
||||
> 在平面中X1点到X2点的距离为其公式为：$$ d(i,j)=|X1-X2|+|Y1-Y2| $$ 转换为程序语言如下，其中Cost为相邻两个节点移动所耗费的代价
|
||||
>
|
||||
> ```
|
||||
> func Manhattan(startX, startY, endX, endY float64) float64 {
|
||||
> dx := math.Abs(startX - endX)
|
||||
> dy := math.Abs(startY - endY)
|
||||
> return Cost * (dx + dy)
|
||||
> }
|
||||
> ```
|
||||
|
||||
> 对角线距离：如果你的地图允许对角线运动，则启发函数可以使用对角距离。它的计算方法如下：
|
||||
>
|
||||
> 其中HVCost是水平、垂直方向移动代价，SCost为倾斜方向移动代价
|
||||
>
|
||||
> ```
|
||||
> func Diagonal(startX, startY, endX, endY float64) float64 {
|
||||
> dx := math.Abs(startX - endX)
|
||||
> dy := math.Abs(startY - endY)
|
||||
> return HVCost*(dx+dy) + (SCost-2*HVCost)* math.Min(dx, dy)
|
||||
> }
|
||||
> ```
|
||||
|
||||
> 欧几里得距离：是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离），其公式为：$$ \sqrt[2]{ (x2−x1)^2+(y2−y1)^2} $$
|
||||
>
|
||||
> 该公式为点(x1,y1)与点(x2,y2)之间的欧氏距离
|
||||
>
|
||||
> ```
|
||||
> func Euclidean(startX, startY, endX, endY float64) float64 {
|
||||
> dx := math.Abs(startX - endX)
|
||||
> dy := math.Abs(startY - endY)
|
||||
> return D * math.Sqrt(dx * dx + dy * dy)
|
||||
> }
|
||||
> ```
|
||||
|
||||
在此文章中我们选择对角距离公式来作为启发函数求*h(n)*的公式。
|
||||
|
||||
启发函数可能对算法造成的影响[^5]：
|
||||
|
||||
•在极端情况下，当启发函数h(n) 始终为0，则将由g(n) 决定节点的优先级，此时算法就退化成了Dijkstra算法。•如果h(n) 始终小于等于节点n到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。•如果h(n) 完全等于节点n到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。•如果h(n)的值比节点n到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。•在另外一个极端情况下，如果h(n)相较于g(n)大很多，则此时只有h(n)产生效果，这也就变成了最佳优先搜索。
|
||||
|
||||
### A Star算法执行过程
|
||||
|
||||
在搜索过程中，A Star算法需要遍历周围8方向的8个节点，并将之有效的节点（即可通过的节点）计算**f(n)\**后放入一个优先级队列中，以便下次循环可以直接取出优先级最高的节点继续遍历，此时我们把这个优先级队列称呼为\*\**\*OpenList\****，另外A Star算法中也需要一个容器用来存储已经遍历过的节点、以防止重复的遍历，那么此时我们把这个容器称之为****CloseList\****。
|
||||
|
||||
接下来本文讲按照步骤说明A Star算法每一步的执行过程：
|
||||
|
||||
1.对***OpenList\**\**和\****CloseList***进行初始化，作者采用小根堆来作为\**\**OpenList\****的实现数据结构，采用HashMap作为****CloseList\****的数据结构，其中Key为节点坐标值Value为空结构体。2.首先确定Start节点以及End节点，而后将Start节点放入****OpenList\****中。3.从****OpenList\****中取出一个节点Cur，如果Cur节点为End节点，则回溯当前节点结构中存储的父节点对象（像链表一样向前回溯）直到父节点对象为nil或者为Start节点，此时得到搜索到的路径，搜索结束返回。4.如果Cur节点非End节点则进行如下逻辑：
|
||||
|
||||
1.将当前X节点放入***CloseList\**\**中，如果在取出Cur节点时未做删除操作的话那么则从\****OpenList***中删除。2.遍历Cur节点其周围8方向的所有额邻居可用节点、可用节点的条件为：
|
||||
|
||||
1.是可通过的节点。2.未处于****CloseList\****中。
|
||||
|
||||
3.计算当前的Cur节点的邻居可用节点，计算其**f(n)\**值，设置其父节点为Cur节点，随后将其加入至\*\**\*OpenList\****中。
|
||||
|
||||
|
||||
|
||||
5.循环执行3-4。直到找不到有效路径或找到End节点。
|
||||
|
||||
|
||||
|
||||
### 代码实现
|
||||
|
||||
本章代码采用Go1.16.2版本实现，主要展示的是搜索业务逻辑部分的代码。
|
||||
|
||||
```
|
||||
// 优先队列
|
||||
type PriorityQueue []*Node
|
||||
|
||||
func (receiver PriorityQueue) Len() int {
|
||||
return len(receiver)
|
||||
}
|
||||
|
||||
func (receiver PriorityQueue) Less(i, j int) bool {
|
||||
return receiver[i].Fn() < receiver[j].Fn()
|
||||
}
|
||||
|
||||
func (receiver PriorityQueue) Swap(i, j int) {
|
||||
receiver[i], receiver[j] = receiver[j], receiver[i]
|
||||
}
|
||||
|
||||
func (receiver *PriorityQueue) Push(x interface{}) {
|
||||
*receiver = append(*receiver, x.(*Node))
|
||||
}
|
||||
|
||||
func (receiver *PriorityQueue) Pop() interface{} {
|
||||
index := len(*receiver)
|
||||
v := (*receiver)[index-1]
|
||||
*receiver = (*receiver)[:index-1]
|
||||
return v
|
||||
}
|
||||
|
||||
// 传入的是一个存放搜索路径的切片
|
||||
// *tools.Node 是节点指针
|
||||
func (receiver *FindAWay) doAStar(result *[]*tools.Node) {
|
||||
for receiver.OpenQueue.Len() > 0 {
|
||||
// 从 OpenList 里取出一个节点
|
||||
node := receiver.openGet()
|
||||
// 看看是不是终点
|
||||
if receiver.end.Equal(node.Position()) {
|
||||
receiver.statistics(node, result)
|
||||
return
|
||||
}
|
||||
// 节点放入CloseList
|
||||
receiver.closePut(node)
|
||||
// 进行具体处理
|
||||
receiver.azimuthProcessing(node)
|
||||
}
|
||||
}
|
||||
|
||||
func (receiver *FindAWay) azimuthProcessing(node *tools.Node) {
|
||||
// 遍历当前节点的8个方向
|
||||
// tools.NodeFormula 是一个存有 计算8个方向坐标的函数数组
|
||||
for azimuth, f := range tools.NodeFormula {
|
||||
// Position 返回一个 存放了 XY字段的结构体代表节点坐标
|
||||
nearNode := tools.GlobalMap.GetNode(f(node.Position()))
|
||||
// 返回为nil代表节点超出边界
|
||||
// EffectiveCoordinate() 代表当前邻居节点是否可用，即是否可以通过
|
||||
if nearNode == nil || !nearNode.EffectiveCoordinate() {
|
||||
continue
|
||||
}
|
||||
// 查看当前邻居节点是否处于 CloseList里
|
||||
if _, ok := receiver.CloseMap[nearNode.Position()]; ok {
|
||||
continue
|
||||
}
|
||||
// 查看当前邻居节点是否处于 OpenList里
|
||||
// 这算是个优化，防止OpenList插入重复节点
|
||||
if _, ok := receiver.OpenMap[nearNode.Position()]; !ok {
|
||||
// 设置当前邻居节点的父节点为当前节点
|
||||
nearNode.SetParent(node)
|
||||
// 根据所处方位使用不同的移动代价计算Fn值
|
||||
|
||||
// 此时 HVCost =10
|
||||
// SCost = HVCost * 1.4
|
||||
switch tools.Azimuth(azimuth) {
|
||||
// 斜方计算
|
||||
case tools.LeftUp, tools.LeftDown, tools.RightUp, tools.RightDown:
|
||||
nearNode.CalcGn(tools.SCost).CalcHn(receiver.end.Position()).CalcFn()
|
||||
// 垂直、水平方向计算
|
||||
default:
|
||||
nearNode.CalcGn(tools.HVCost).CalcHn(receiver.end.Position()).CalcFn()
|
||||
}
|
||||
// 将当前邻居节点放入OpenList中
|
||||
receiver.openPut(nearNode)
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### 结果测试
|
||||
|
||||
由于没有找到比较方便的实时现实库，所以就拿Excel做了一下，下面两个图为地图以及搜索后的结果图。
|
||||
|
||||
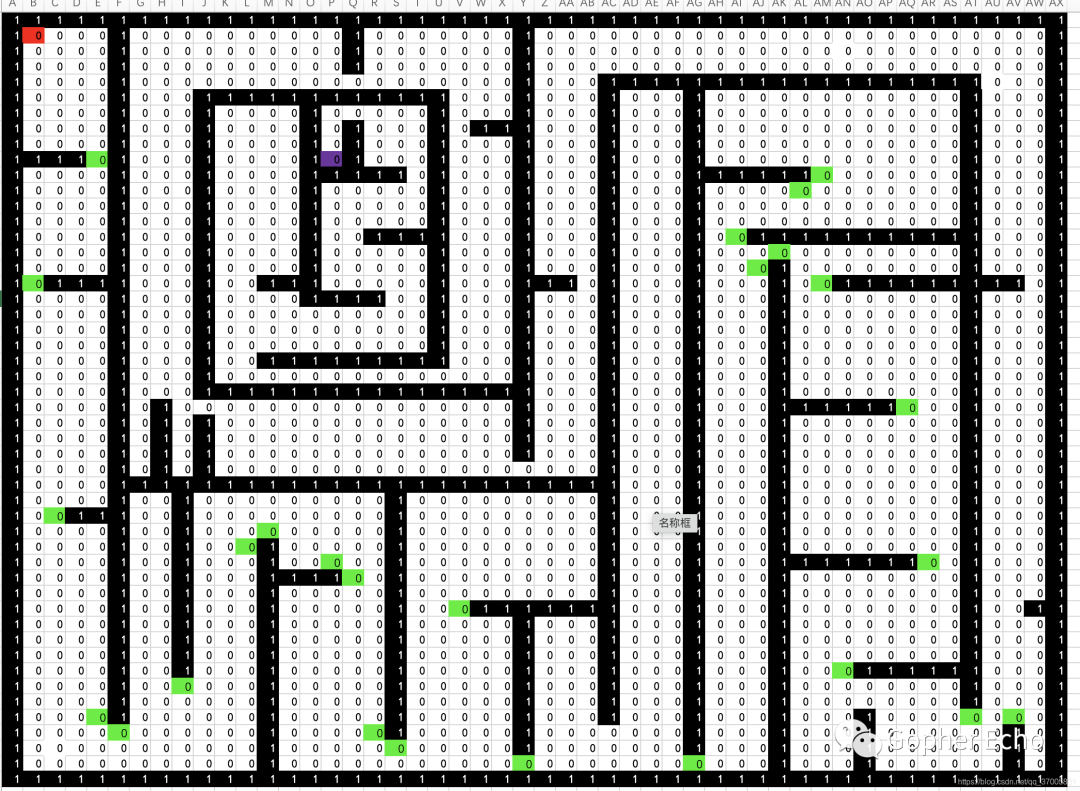
1为墙。
|
||||
|
||||
0为可通过的点。
|
||||
|
||||
5为得到的路径。
|
||||
|
||||
红色为起点
|
||||
|
||||
紫色为终点
|
||||
|
||||
绿色忘记删了，没有代表意义
|
||||
|
||||
下图为原地图：
|
||||
|
||||
|
||||
|
||||
下图为搜寻完毕的地图：
|
||||
|
||||
## 总结
|
||||
|
||||
A Star算法算是一个很简单的用于游戏中自动寻路的算法，但是其性能还有有些问题，主要问题在于其需要把每个节点的周围所有可用节点均插入**OpenList\**中，因此相对来说性能损耗几乎都在这个\****OpenList***中，因此A Star算法有很多对其可以优化的算法。
|
||||
|
||||
日后作者将会写一篇关于针对A Star的优化算法即：JPS（jump point search）算法，该算法实际上是对A Star寻路算法的一个改进，A Star 算法在扩展节点时会把节点所有邻居都考虑进去，这样***OpenList\**\**中点的数量会很多，搜索效率较慢。而JPS在A Star算法模型的基础之上，优化了搜索后继节点的操作。A Star的处理是把周边能搜索到的格子，加进OpenList，然后在OpenList中弹出最小值。JPS也是这样的操作，但相对于A Star来说，JPS操作\****OpenList***的次数很少，它会先用一种更高效的方法来搜索需要加进\**\**OpenList\****的节点，从而减少****OpenList\****中节点的数量。
|
||||
|
||||
[^1]: Dijkstra算法 https://baike.baidu.com/item/%E8%BF%AA%E5%85%8B%E6%96%AF%E7%89%B9%E6%8B%89%E7%AE%97%E6%B3%95/23665989?fromtitle=Dijkstra%E7%AE%97%E6%B3%95&fromid=215612 [^2]: Cormen, Thomas H.[1]; Leiserson, Charles E.[2]; Rivest, Ronald L.[3]; Stein, Clifford[4]. Section 24.3: Dijkstra's algorithm. Introduction to Algorithms[5] Second. MIT Press[6] and McGraw–Hill[7]. 2001: 595–601. ISBN 0-262-03293-7[8]. [^3]: 最佳优先搜索算法（Best-First-Search） https://www.jianshu.com/p/9873372fe4b4 [^4]: A Star算法 https://zh.wikipedia.org/wiki/A*%E6%90%9C%E5%B0%8B%E6%BC%94%E7%AE%97%E6%B3%95 [^5]: 路径规划之 A* 算法 https://paul.pub/a-star-algorithm/#id-dijkstra%E7%AE%97%E6%B3%95
|
||||
|
||||
### References
|
||||
618
source/_posts/algorithm/graph/union_find/并查集算法.md
Normal file
618
source/_posts/algorithm/graph/union_find/并查集算法.md
Normal file
@ -0,0 +1,618 @@
|
||||
---
|
||||
title: Union-Find 算法
|
||||
date: 2024-3-19
|
||||
tag:
|
||||
- 算法
|
||||
- 并查集
|
||||
- 图
|
||||
categories: 算法
|
||||
abbrlink: e88a2bb0
|
||||
---
|
||||
|
||||
# Union-Find 算法（并查集算法）
|
||||
|
||||
## ⼀、问题介绍
|
||||
|
||||
简单说，动态连通性其实可以抽象成给⼀幅图连线。⽐如下⾯这幅图，总共
|
||||
|
||||
有 10 个节点，他们互不相连，分别⽤ 0~9 标记：
|
||||
|
||||
|
||||
|
||||
现在我们的 Union-Find 算法主要需要实现这两个 API：
|
||||
|
||||
```java
|
||||
class UF {
|
||||
/* 将 p 和 q 连接 */
|
||||
public void union(int p, int q);
|
||||
/* 判断 p 和 q 是否连通 */
|
||||
public boolean connected(int p, int q);
|
||||
/* 返回图中有多少个连通分量 */
|
||||
public int count();
|
||||
}
|
||||
```
|
||||
|
||||
这⾥所说的「连通」是⼀种等价关系，也就是说具有如下三个性质：
|
||||
|
||||
1、⾃反性：节点 p 和 p 是连通的。
|
||||
|
||||
2、对称性：如果节点 p 和 q 连通，那么 q 和 p 也连通。
|
||||
|
||||
3、传递性：如果节点 p 和 q 连通， q 和 r 连通，那么 p 和 r 也连通。
|
||||
|
||||
⽐如说之前那幅图，0〜9 任意两个不同的点都不连通，调⽤ connected 都
|
||||
|
||||
会返回 false，连通分量为 10 个。
|
||||
|
||||
如果现在调⽤ union(0, 1) ，那么 0 和 1 被连通，连通分量降为 9 个。
|
||||
|
||||
再调⽤ union(1, 2) ，这时 0,1,2 都被连通，调⽤ connected(0, 2) 也会返回
|
||||
|
||||
true，连通分量变为 8 个。
|
||||
|
||||
|
||||
|
||||
判断这种「等价关系」⾮常实⽤，⽐如说编译器判断同⼀个变量的不同引
|
||||
|
||||
⽤，⽐如社交⽹络中的朋友圈计算等等。
|
||||
|
||||
这样，你应该⼤概明⽩什么是动态连通性了，Union-Find 算法的关键就在
|
||||
|
||||
于 union 和 connected 函数的效率。那么⽤什么模型来表⽰这幅图的连通状
|
||||
|
||||
态呢？⽤什么数据结构来实现代码呢？
|
||||
|
||||
## ⼆、基本思路
|
||||
|
||||
注意我刚才把「模型」和具体的「数据结构」分开说，这么做是有原因的。
|
||||
|
||||
因为我们使⽤森林（若⼲棵树）来表⽰图的动态连通性，⽤数组来具体实现
|
||||
|
||||
这个森林。
|
||||
|
||||
怎么⽤森林来表⽰连通性呢？我们设定树的每个节点有⼀个指针指向其⽗节
|
||||
|
||||
点，如果是根节点的话，这个指针指向⾃⼰。⽐如说刚才那幅 10 个节点的
|
||||
|
||||
图，⼀开始的时候没有相互连通，就是这样：
|
||||
|
||||
|
||||
|
||||
```java
|
||||
class UF {
|
||||
// 记录连通分量
|
||||
private int count;
|
||||
// 节点 x 的节点是 parent[x]
|
||||
private int[] parent;
|
||||
/* 构造函数，n 为图的节点总数 */
|
||||
public UF(int n) {
|
||||
// ⼀开始互不连通
|
||||
this.count = n;
|
||||
// ⽗节点指针初始指向⾃⼰
|
||||
parent = new int[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
parent[i] = i;
|
||||
}
|
||||
}
|
||||
/* 其他函数 */
|
||||
}
|
||||
```
|
||||
|
||||
如果某两个节点被连通，则让其中的（任意）⼀个节点的根节点接到另⼀个
|
||||
|
||||
节点的根节点上：
|
||||
|
||||
|
||||
|
||||
```java
|
||||
public void union(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
if (rootP == rootQ)
|
||||
return;
|
||||
// 将两棵树合并为⼀棵
|
||||
parent[rootP] = rootQ;
|
||||
// parent[rootQ] = rootP 也⼀样
|
||||
count--; // 两个分量合⼆为⼀
|
||||
}
|
||||
/* 返回某个节点 x 的根节点 */
|
||||
private int find(int x) {
|
||||
// 根节点的 parent[x] == x
|
||||
while (parent[x] != x)
|
||||
x = parent[x];
|
||||
return x;
|
||||
}
|
||||
/* 返回当前的连通分量个数 */
|
||||
public int count() {
|
||||
return count;
|
||||
}
|
||||
```
|
||||
|
||||
这样，如果节点 p 和 q 连通的话，它们⼀定拥有相同的根节点：
|
||||
|
||||
|
||||
|
||||
```java
|
||||
public boolean connected(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
return rootP == rootQ;
|
||||
}
|
||||
```
|
||||
|
||||
⾄此，Union-Find 算法就基本完成了。是不是很神奇？竟然可以这样使⽤数
|
||||
|
||||
组来模拟出⼀个森林，如此巧妙的解决这个⽐较复杂的问题！
|
||||
|
||||
那么这个算法的复杂度是多少呢？我们发现，主要
|
||||
|
||||
API connected 和 union 中的复杂度都是 find 函数造成的，所以说它们的
|
||||
|
||||
复杂度和 find ⼀样。
|
||||
|
||||
find 主要功能就是从某个节点向上遍历到树根，其时间复杂度就是树的⾼
|
||||
|
||||
度。我们可能习惯性地认为树的⾼度就是 logN ，但这并不⼀定。 logN 的
|
||||
|
||||
⾼度只存在于平衡⼆叉树，对于⼀般的树可能出现极端不平衡的情况，使得
|
||||
|
||||
「树」⼏乎退化成「链表」，树的⾼度最坏情况下可能变成 N 。
|
||||
|
||||
|
||||
|
||||
所以说上⾯这种解法， find , union , connected 的时间复杂度都是 O(N)。
|
||||
|
||||
这个复杂度很不理想的，你想图论解决的都是诸如社交⽹络这样数据规模巨
|
||||
|
||||
⼤的问题，对于 union 和 connected 的调⽤⾮常频繁，每次调⽤需要线性时
|
||||
|
||||
间完全不可忍受。
|
||||
|
||||
问题的关键在于，如何想办法避免树的不平衡呢？只需要略施⼩计即可。
|
||||
|
||||
## 三、平衡性优化
|
||||
|
||||
我们要知道哪种情况下可能出现不平衡现象，关键在于 union 过程：
|
||||
|
||||
```java
|
||||
public void union(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
if (rootP == rootQ)
|
||||
return;
|
||||
// 将两棵树合并为⼀棵
|
||||
parent[rootP] = rootQ;
|
||||
// parent[rootQ] = rootP 也可以
|
||||
count--;
|
||||
//......
|
||||
}
|
||||
```
|
||||
|
||||
我们⼀开始就是简单粗暴的把 p 所在的树接到 q 所在的树的根节点下⾯，
|
||||
|
||||
那么这⾥就可能出现「头重脚轻」的不平衡状况，⽐如下⾯这种局⾯：
|
||||
|
||||
|
||||
|
||||
⻓此以往，树可能⽣⻓得很不平衡。我们其实是希望，⼩⼀些的树接到⼤⼀
|
||||
|
||||
些的树下⾯，这样就能避免头重脚轻，更平衡⼀些。解决⽅法是额外使⽤⼀
|
||||
|
||||
个 size 数组，记录每棵树包含的节点数，我们不妨称为「重量」：
|
||||
|
||||
```java
|
||||
class UF {
|
||||
private int count;
|
||||
private int[] parent;
|
||||
// 新增⼀个数组记录树的“重量”
|
||||
private int[] size;
|
||||
public UF(int n) {
|
||||
this.count = n;
|
||||
parent = new int[n];
|
||||
// 最初每棵树只有⼀个节点
|
||||
// 重量应该初始化 1
|
||||
size = new int[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
parent[i] = i; size[i] = 1;
|
||||
}
|
||||
}
|
||||
/* 其他函数 */
|
||||
}
|
||||
```
|
||||
|
||||
⽐如说 size[3] = 5 表⽰，以节点 3 为根的那棵树，总共有 5 个节点。这
|
||||
|
||||
样我们可以修改⼀下 union ⽅法：
|
||||
|
||||
```java
|
||||
public void union(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
if (rootP == rootQ)
|
||||
return;
|
||||
// ⼩树接到⼤树下⾯，较平衡
|
||||
if (size[rootP] > size[rootQ]) {
|
||||
parent[rootQ] = rootP; size[rootP] += size[rootQ];
|
||||
} else {
|
||||
parent[rootP] = rootQ; size[rootQ] += size[rootP];
|
||||
}
|
||||
count--;
|
||||
}
|
||||
```
|
||||
|
||||
这样，通过⽐较树的重量，就可以保证树的⽣⻓相对平衡，树的⾼度⼤致
|
||||
|
||||
在 logN 这个数量级，极⼤提升执⾏效率。
|
||||
|
||||
此时， find , union , connected 的时间复杂度都下降为 O(logN)，即便数据
|
||||
|
||||
规模上亿，所需时间也⾮常少
|
||||
|
||||
## 四、路径压缩
|
||||
|
||||
这步优化特别简单，所以⾮常巧妙。我们能不能进⼀步压缩每棵树的⾼度，
|
||||
|
||||
使树⾼始终保持为常数？
|
||||
|
||||
|
||||
|
||||
这样 find 就能以 O(1) 的时间找到某⼀节点的根节点，相应
|
||||
|
||||
的， connected 和 union 复杂度都下降为 O(1)。
|
||||
|
||||
要做到这⼀点，⾮常简单，只需要在 find 中加⼀⾏代码：
|
||||
|
||||
```java
|
||||
private int find(int x) {
|
||||
while (parent[x] != x) {
|
||||
// 进⾏路径压缩
|
||||
parent[x] = parent[parent[x]];
|
||||
x = parent[x];
|
||||
}
|
||||
return x;
|
||||
}
|
||||
```
|
||||
|
||||
这个操作有点匪夷所思，看个 GIF 就明⽩它的作⽤了（为清晰起⻅，这棵
|
||||
|
||||
树⽐较极端）：
|
||||
|
||||
|
||||
|
||||
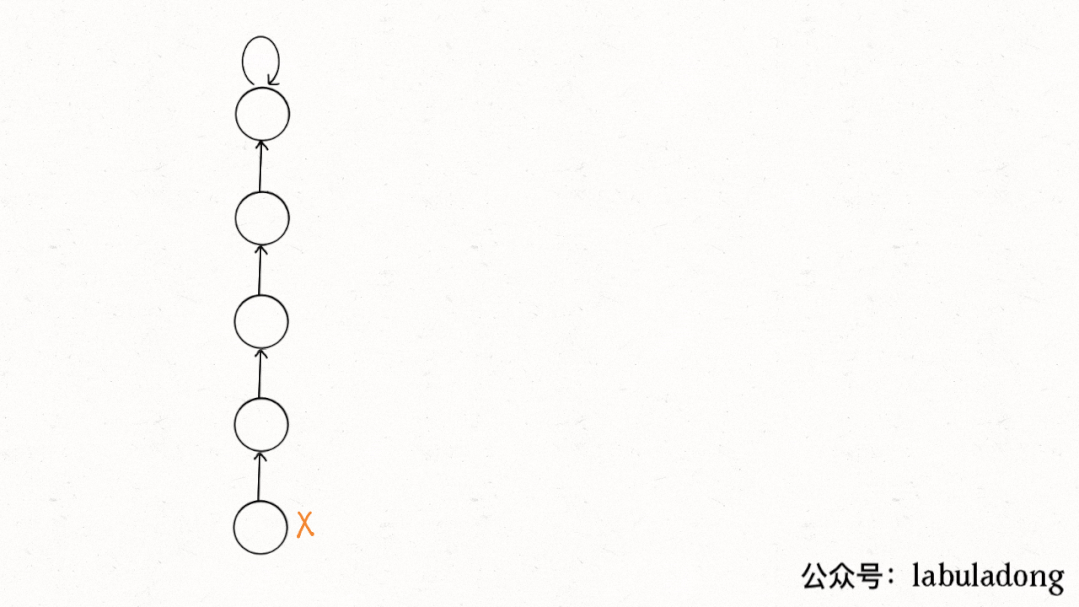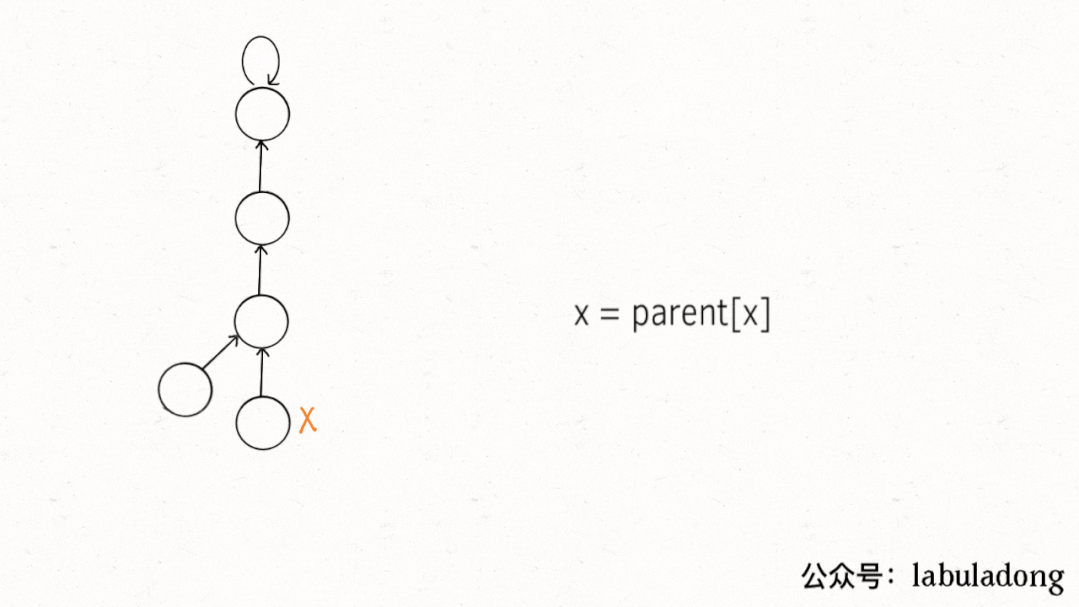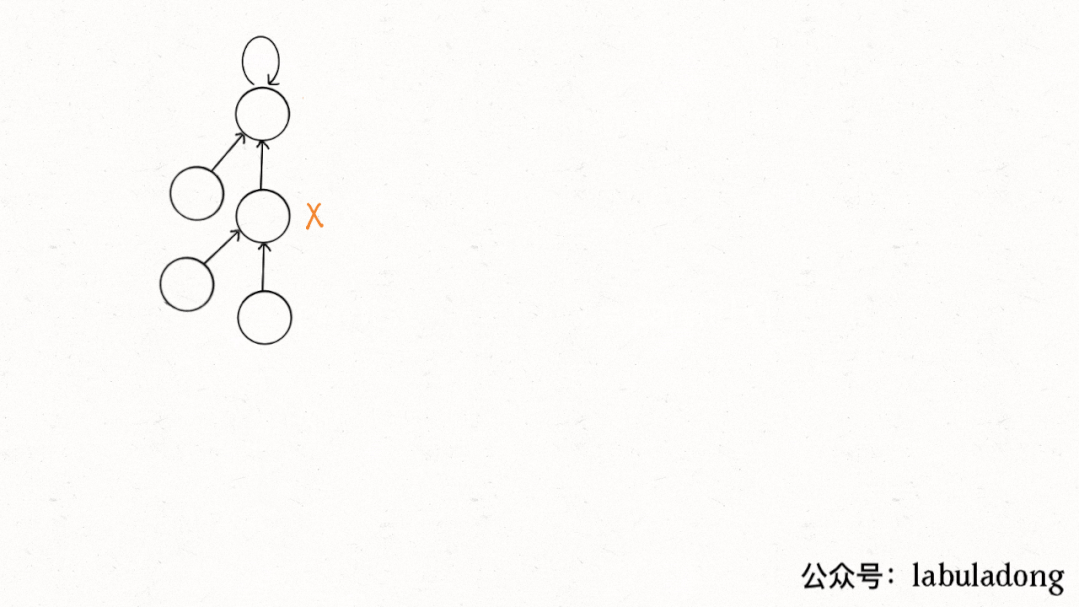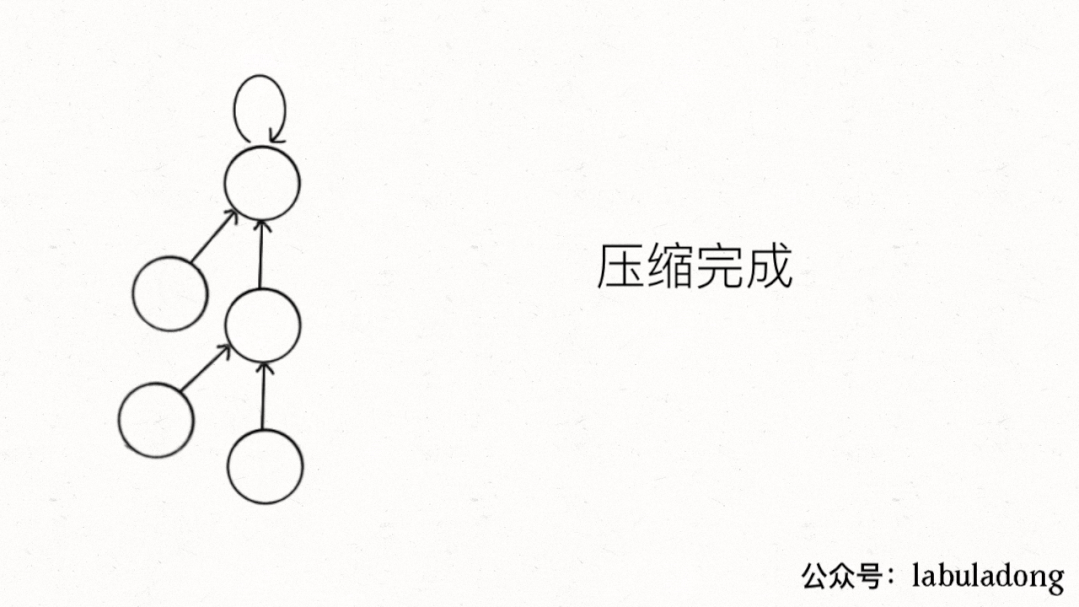
用语言描述就是，每次 while 循环都会把一对儿父子节点改到同一层，这样每次调用`find`函数向树根遍历的同时，顺手就将树高缩短了，最终所有树高都会是一个常数，那么所有方法的复杂度也就都是 O(1)。
|
||||
|
||||
> PS：读者可能会问，这个 GIF 图的`find`过程完成之后，树高确实缩短了，但是如果更高的树，压缩后高度可能依然很大呀？不能这么想。因为这个 GIF 的情景是我编出来方便大家理解路径压缩的，但是实际中，每次`find`都会进行路径压缩，所以树本来就不可能增长到这么高，这种担心是多余的。
|
||||
|
||||
路径压缩的第二种写法是这样：
|
||||
|
||||
```java
|
||||
// 第二种路径压缩的 find 方法
|
||||
public int find(int x) {
|
||||
if (parent[x] != x) {
|
||||
parent[x] = find(parent[x]);
|
||||
}
|
||||
return parent[x];
|
||||
}
|
||||
```
|
||||
|
||||
我一度认为这种递归写法和第一种迭代写法做的事情一样，但实际上是我大意了，有读者指出这种写法进行路径压缩的效率是高于上一种解法的。
|
||||
|
||||
这个递归过程有点不好理解，你可以自己手画一下递归过程。我把这个函数做的事情翻译成迭代形式，方便你理解它进行路径压缩的原理：
|
||||
|
||||
```java
|
||||
// 这段迭代代码方便你理解递归代码所做的事情
|
||||
public int find(int x) {
|
||||
// 先找到根节点
|
||||
int root = x;
|
||||
while (parent[root] != root) {
|
||||
root = parent[root];
|
||||
}
|
||||
// 然后把 x 到根节点之间的所有节点直接接到根节点下面
|
||||
int old_parent = parent[x];
|
||||
while (x != root) {
|
||||
parent[x] = root;
|
||||
x = old_parent;
|
||||
old_parent = parent[old_parent];
|
||||
}
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
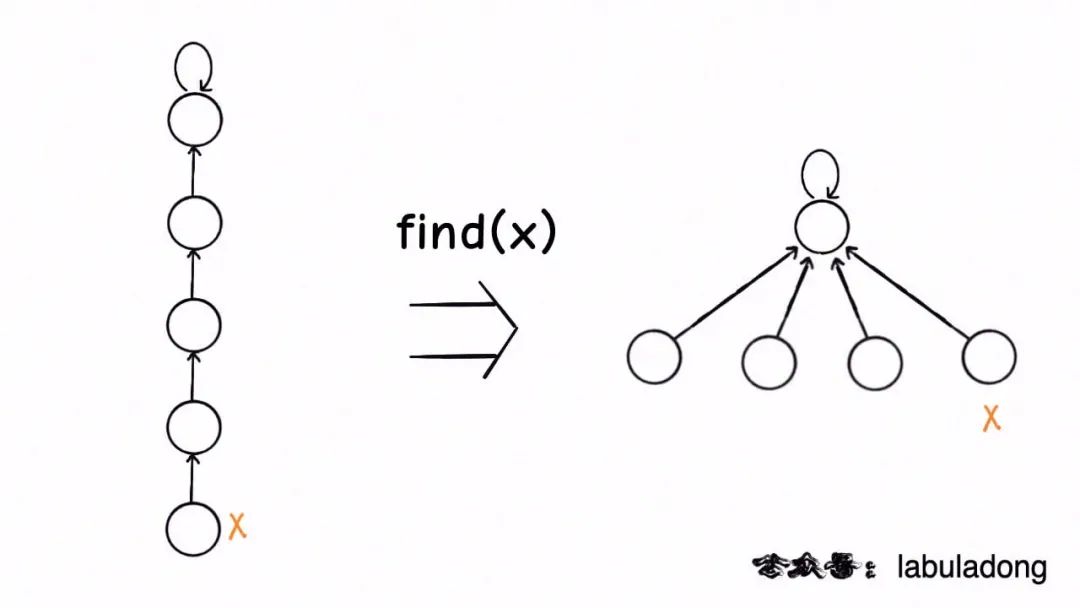
这种路径压缩的效果如下：
|
||||
|
||||
|
||||
|
||||
比起第一种路径压缩，显然这种方法压缩得更彻底，直接把一整条树枝压平，一点意外都没有，所以从效率的角度来说，推荐你使用这种路径压缩算法。
|
||||
|
||||
**另外，如果路径压缩技巧将树高保持为常数了，那么`size`数组的平衡优化就不是特别必要了**。
|
||||
|
||||
所以你一般看到的 Union Find 算法应该是如下实现：
|
||||
|
||||
```java
|
||||
class UF {
|
||||
// 连通分量个数
|
||||
private int count;
|
||||
// 存储每个节点的父节点
|
||||
private int[] parent;
|
||||
|
||||
// n 为图中节点的个数
|
||||
public UF(int n) {
|
||||
this.count = n;
|
||||
parent = new int[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
parent[i] = i;
|
||||
}
|
||||
}
|
||||
|
||||
// 将节点 p 和节点 q 连通
|
||||
public void union(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
if (rootP == rootQ)
|
||||
return;
|
||||
parent[rootQ] = rootP;
|
||||
// 两个连通分量合并成一个连通分量
|
||||
count--;
|
||||
}
|
||||
|
||||
// 判断节点 p 和节点 q 是否连通
|
||||
public boolean connected(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
return rootP == rootQ;
|
||||
}
|
||||
|
||||
public int find(int x) {
|
||||
if (parent[x] != x) {
|
||||
parent[x] = find(parent[x]);
|
||||
}
|
||||
return parent[x];
|
||||
}
|
||||
|
||||
// 返回图中的连通分量个数
|
||||
public int count() {
|
||||
return count;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Union-Find 算法的复杂度可以这样分析：构造函数初始化数据结构需要 O(N) 的时间和空间复杂度；连通两个节点`union`、判断两个节点的连通性`connected`、计算连通分量`count`所需的时间复杂度均为 O(1)。
|
||||
|
||||
到这里，相信你已经掌握了 Union-Find 算法的核心逻辑，总结一下我们优化算法的过程：
|
||||
|
||||
1、用`parent`数组记录每个节点的父节点，相当于指向父节点的指针，所以`parent`数组内实际存储着一个森林（若干棵多叉树）。
|
||||
|
||||
2、用`size`数组记录着每棵树的重量，目的是让`union`后树依然拥有平衡性，保证各个 API 时间复杂度为 O(logN)，而不会退化成链表影响操作效率。
|
||||
|
||||
3、在`find`函数中进行路径压缩，保证任意树的高度保持在常数，使得各个 API 时间复杂度为 O(1)。使用了路径压缩之后，可以不使用`size`数组的平衡优化。
|
||||
|
||||
下面我们看一些具体的并查集题目。
|
||||
|
||||
## 五、题目实践
|
||||
|
||||
力扣第 323 题「无向图中连通分量的数目」就是最基本的连通分量题目：
|
||||
|
||||
给你输入一个包含`n`个节点的图，用一个整数`n`和一个数组`edges`表示，其中`edges[i] = [ai, bi]`表示图中节点`ai`和`bi`之间有一条边。请你计算这幅图的连通分量个数。
|
||||
|
||||
函数签名如下：
|
||||
|
||||
```java
|
||||
int countComponents(int n, int[][] edges)
|
||||
```
|
||||
|
||||
这道题我们可以直接套用`UF`类来解决：
|
||||
|
||||
```java
|
||||
public int countComponents(int n, int[][] edges) {
|
||||
UF uf = new UF(n);
|
||||
// 将每个节点进行连通
|
||||
for (int[] e : edges) {
|
||||
uf.union(e[0], e[1]);
|
||||
}
|
||||
// 返回连通分量的个数
|
||||
return uf.count();
|
||||
}
|
||||
|
||||
class UF {
|
||||
// 见上文
|
||||
}
|
||||
```
|
||||
|
||||
****另外，一些使用 DFS 深度优先算法解决的问题，也可以用 Union-Find 算法解决**。
|
||||
|
||||
比如力扣第 130 题「被围绕的区域」：
|
||||
|
||||
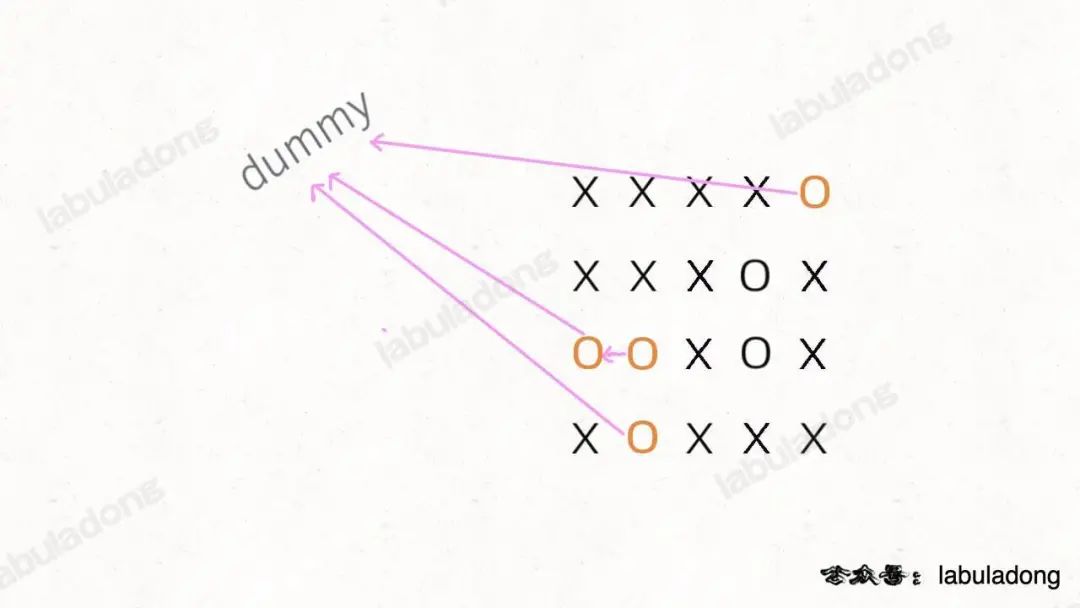
给你一个 M×N 的二维矩阵，其中包含字符`X`和`O`，让你找到矩阵中**四面**被`X`围住的`O`，并且把它们替换成`X`。
|
||||
|
||||
```java
|
||||
void solve(char[][] board);
|
||||
```
|
||||
|
||||
注意哦，必须是四面被围的`O`才能被换成`X`，也就是说边角上的`O`一定不会被围，进一步，与边角上的`O`相连的`O`也不会被`X`围四面，也不会被替换。**
|
||||
|
||||
|
||||
|
||||
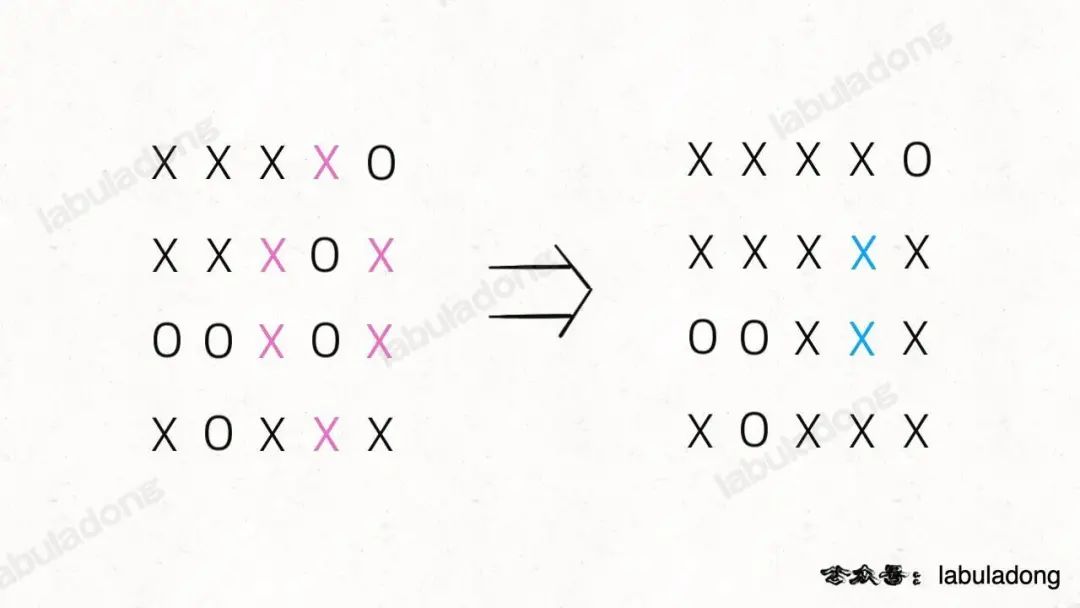
> PS：这让我想起小时候玩的棋类游戏「黑白棋」，只要你用两个棋子把对方的棋子夹在中间，对方的子就被替换成你的子。可见，占据四角的棋子是无敌的，与其相连的边棋子也是无敌的（无法被夹掉）。
|
||||
|
||||
其实这个问题应该归为 [岛屿系列问题](https://mp.weixin.qq.com/s?__biz=MzAxODQxMDM0Mw==&mid=2247492234&idx=1&sn=fef28b1ca7639e056104374ddc9fbf0b&scene=21#wechat_redirect) 使用 DFS 算法解决：
|
||||
|
||||
先用 for 循环遍历棋盘的**四边**，用 DFS 算法把那些与边界相连的`O`换成一个特殊字符，比如`#`；然后再遍历整个棋盘，把剩下的`O`换成`X`，把`#`恢复成`O`。这样就能完成题目的要求，时间复杂度 O(MN)。
|
||||
|
||||
但这个问题也可以用 Union-Find 算法解决，虽然实现复杂一些，甚至效率也略低，但这是使用 Union-Find 算法的通用思想，值得一学。
|
||||
|
||||
**你可以把那些不需要被替换的`O`看成一个拥有独门绝技的门派，它们有一个共同「祖师爷」叫`dummy`，这些`O`和`dummy`互相连通，而那些需要被替换的`O`与`dummy`不连通**。
|
||||
|
||||
|
||||
|
||||
这就是 Union-Find 的核心思路，明白这个图，就很容易看懂代码了。
|
||||
|
||||
首先要解决的是，根据我们的实现，Union-Find 底层用的是一维数组，构造函数需要传入这个数组的大小，而题目给的是一个二维棋盘。
|
||||
|
||||
这个很简单，二维坐标`(x,y)`可以转换成`x * n + y`这个数（`m`是棋盘的行数，`n`是棋盘的列数），**敲黑板，这是将二维坐标映射到一维的常用技巧**。
|
||||
|
||||
其次，我们之前描述的「祖师爷」是虚构的，需要给他老人家留个位置。索引`[0.. m*n-1]`都是棋盘内坐标的一维映射，那就让这个虚拟的`dummy`节点占据索引`m * n`好了。
|
||||
|
||||
看解法代码：
|
||||
|
||||
```java
|
||||
void solve(char[][] board) {
|
||||
if (board.length == 0) return;
|
||||
|
||||
int m = board.length;
|
||||
int n = board[0].length;
|
||||
// 给 dummy 留一个额外位置
|
||||
UF uf = new UF(m * n + 1);
|
||||
int dummy = m * n;
|
||||
// 将首列和末列的 O 与 dummy 连通
|
||||
for (int i = 0; i < m; i++) {
|
||||
if (board[i][0] == 'O')
|
||||
uf.union(i * n, dummy);
|
||||
if (board[i][n - 1] == 'O')
|
||||
uf.union(i * n + n - 1, dummy);
|
||||
}
|
||||
// 将首行和末行的 O 与 dummy 连通
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (board[0][j] == 'O')
|
||||
uf.union(j, dummy);
|
||||
if (board[m - 1][j] == 'O')
|
||||
uf.union(n * (m - 1) + j, dummy);
|
||||
}
|
||||
// 方向数组 d 是上下左右搜索的常用手法
|
||||
int[][] d = new int[][]{{1,0}, {0,1}, {0,-1}, {-1,0}};
|
||||
for (int i = 1; i < m - 1; i++)
|
||||
for (int j = 1; j < n - 1; j++)
|
||||
if (board[i][j] == 'O')
|
||||
// 将此 O 与上下左右的 O 连通
|
||||
for (int k = 0; k < 4; k++) {
|
||||
int x = i + d[k][0];
|
||||
int y = j + d[k][1];
|
||||
if (board[x][y] == 'O')
|
||||
uf.union(x * n + y, i * n + j);
|
||||
}
|
||||
// 所有不和 dummy 连通的 O，都要被替换
|
||||
for (int i = 1; i < m - 1; i++)
|
||||
for (int j = 1; j < n - 1; j++)
|
||||
if (!uf.connected(dummy, i * n + j))
|
||||
board[i][j] = 'X';
|
||||
}
|
||||
|
||||
class UF {
|
||||
// 见上文
|
||||
}
|
||||
```
|
||||
|
||||
这段代码很长，其实就是刚才的思路实现，只有和边界`O`相连的`O`才具有和`dummy`的连通性，他们不会被替换。
|
||||
|
||||
其实用 Union-Find 算法解决这个简单的问题有点杀鸡用牛刀，它可以解决更复杂，更具有技巧性的问题，**主要思路是适时增加虚拟节点，想办法让元素「分门别类」，建立动态连通关系**。
|
||||
|
||||
力扣第 990 题「等式方程的可满足性」用 Union-Find 算法就显得十分优美了，题目是这样：
|
||||
|
||||
给你一个数组`equations`，装着若干字符串表示的算式。每个算式`equations[i]`长度都是 4，而且只有这两种情况：`a==b`或者`a!=b`，其中`a,b`可以是任意小写字母。你写一个算法，如果`equations`中所有算式都不会互相冲突，返回 true，否则返回 false。
|
||||
|
||||
比如说，输入`["a==b","b!=c","c==a"]`，算法返回 false，因为这三个算式不可能同时正确。
|
||||
|
||||
再比如，输入`["c==c","b==d","x!=z"]`，算法返回 true，因为这三个算式并不会造成逻辑冲突。
|
||||
|
||||
我们前文说过，动态连通性其实就是一种等价关系，具有「自反性」「传递性」和「对称性」，其实`==` 关系也是一种等价关系，具有这些性质。所以这个问题用 Union-Find 算法就很自然。
|
||||
|
||||
**核心思想是，将`equations`中的算式根据`==`和`!=`分成两部分，先处理`==`算式，使得他们通过相等关系各自勾结成门派（连通分量）；然后处理`!=`算式，检查不等关系是否破坏了相等关系的连通性**。
|
||||
|
||||
```java
|
||||
boolean equationsPossible(String[] equations) {
|
||||
// 26 个英文字母
|
||||
UF uf = new UF(26);
|
||||
// 先让相等的字母形成连通分量
|
||||
for (String eq : equations) {
|
||||
if (eq.charAt(1) == '=') {
|
||||
char x = eq.charAt(0);
|
||||
char y = eq.charAt(3);
|
||||
uf.union(x - 'a', y - 'a');
|
||||
}
|
||||
}
|
||||
// 检查不等关系是否打破相等关系的连通性
|
||||
for (String eq : equations) {
|
||||
if (eq.charAt(1) == '!') {
|
||||
char x = eq.charAt(0);
|
||||
char y = eq.charAt(3);
|
||||
// 如果相等关系成立，就是逻辑冲突
|
||||
if (uf.connected(x - 'a', y - 'a'))
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
class UF {
|
||||
// 见上文
|
||||
}
|
||||
```
|
||||
|
||||
至此，这道判断算式合法性的问题就解决了，借助 Union-Find 算法，是不是很简单呢？
|
||||
|
||||
最后，Union-Find 算法也会在一些其他经典图论算法中用到，比如判断「图」和「树」，以及最小生成树的计算，详情见 [Kruskal 最小生成树算法](https://mp.weixin.qq.com/s?__biz=MzAxODQxMDM0Mw==&mid=2247492575&idx=1&sn=bf63eb391351a0dfed0d03e1ac5992e7&scene=21#wechat_redirect)。
|
||||
|
||||
## 六、最后总结
|
||||
|
||||
我们先来看⼀下完整代码：
|
||||
|
||||
```java
|
||||
class UF {
|
||||
// 连通分量个数
|
||||
private int count;
|
||||
// 存储⼀棵树
|
||||
private int[] parent;
|
||||
// 记录树的“重量”
|
||||
private int[] size;
|
||||
|
||||
public UF(int n) {
|
||||
this.count = n;
|
||||
parent = new int[n];
|
||||
size = new int[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
parent[i] = i;
|
||||
size[i] = 1;
|
||||
}
|
||||
}
|
||||
|
||||
public void union(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
if (rootP == rootQ)
|
||||
return;
|
||||
// ⼩树接到⼤树下⾯，较平衡
|
||||
if (size[rootP] > size[rootQ]) {
|
||||
parent[rootQ] = rootP;
|
||||
size[rootP] += size[rootQ];
|
||||
} else {
|
||||
parent[rootP] = rootQ;
|
||||
size[rootQ] += size[rootP];
|
||||
}
|
||||
count--;
|
||||
}
|
||||
|
||||
public boolean connected(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
return rootP == rootQ;
|
||||
}
|
||||
|
||||
private int find(int x) {
|
||||
while (parent[x] != x) {
|
||||
// 进⾏路径压缩
|
||||
parent[x] = parent[parent[x]];
|
||||
x = parent[x];
|
||||
}
|
||||
return x;
|
||||
}
|
||||
|
||||
public int count() {
|
||||
return count;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
Union-Find 算法的复杂度可以这样分析：构造函数初始化数据结构需要
|
||||
|
||||
O(N) 的时间和空间复杂度；连通两个节点 union 、判断两个节点的连通
|
||||
|
||||
性 connected 、计算连通分量 count 所需的时间复杂度均为 O(1)。
|
||||
Binary file not shown.
|
After Width: | Height: | Size: 235 KiB |
Binary file not shown.
|
After Width: | Height: | Size: 250 KiB |
Binary file not shown.
|
After Width: | Height: | Size: 217 KiB |
Binary file not shown.
|
After Width: | Height: | Size: 255 KiB |
Binary file not shown.
|
After Width: | Height: | Size: 253 KiB |
Binary file not shown.
|
After Width: | Height: | Size: 238 KiB |
Binary file not shown.
|
After Width: | Height: | Size: 259 KiB |
Binary file not shown.
|
After Width: | Height: | Size: 221 KiB |
272
source/_posts/c++/article/2022/02/07/CPlusPlus编码优化之减少冗余拷贝或赋值.md
Normal file
272
source/_posts/c++/article/2022/02/07/CPlusPlus编码优化之减少冗余拷贝或赋值.md
Normal file
@ -0,0 +1,272 @@
|
||||
---
|
||||
title: C++编码优化之减少冗余拷贝或赋值
|
||||
tag:
|
||||
- c++
|
||||
categories: c++
|
||||
abbrlink: 97da918c
|
||||
---
|
||||
|
||||
# C++编码优化之减少冗余拷贝或赋值
|
||||
|
||||
## 临时变量
|
||||
|
||||
目前遇到的一些产生临时变量的情况：函数实参、函数返回值、隐式类型转换、多余的拷贝。
|
||||
|
||||
### 1. 函数实参
|
||||
|
||||
这点应该比较容易理解，函数参数，如果是实参传递的话，函数体里的修改并不会影响调用时传入的参数的值。那么函数体里操作的对象肯定是函数调用的过程中产生出来的。
|
||||
|
||||
那么这种情况我们该怎么办呢？
|
||||
|
||||
如果 `callee` 中确实要修改这个对象，但是 `caller` 又不想 `callee` 的修改影响到原来的值，那么这个临时变量就是必须的了，不需要也没办法避免。
|
||||
|
||||
如果 `callee`中根本没有修改这个对象，或者 `callee` 中这个参数本身就是 `const` 型的，那么将实参传递改为引用传递是个不错的选择（如果是基本类型的函数实参，则没有必要改为引用），可以减少一个临时变量而且不会带来任何损失。
|
||||
|
||||
另外，推荐一个静态代码检查工具 `cppcheck`，这个工具可以提示非基本类型的 `const` 实参改为引用。
|
||||
|
||||
### 2. 函数返回值（返回对象）
|
||||
|
||||
函数返回值的情况比较复杂，因为编译器在这方面做了很多优化，编译器优化到何种程度我也没追根究底研究过。
|
||||
|
||||
在没开任何优化选项的时候，`gcc` 也优化了一些简单的返回对象的情况。
|
||||
|
||||
先看一段代码：
|
||||
|
||||
```
|
||||
A createA(int a)
|
||||
{
|
||||
A tmp;
|
||||
tmp._a=a;
|
||||
return tmp;
|
||||
}
|
||||
```
|
||||
|
||||
抛开所有优化不谈，函数中 `createA` 应该有一个构造操作（`tmp` 对象生成）和一个拷贝构造操作（`tmp` 对象返回时）。
|
||||
|
||||
于是有些编译器尝试对函数返回时的拷贝构造进行优化：
|
||||
|
||||
```
|
||||
A createA(int a)
|
||||
{
|
||||
return A(a);
|
||||
}
|
||||
```
|
||||
|
||||
第一步可以被优化的拷贝构造就是上面的这种情况，即 `RVO(return value optimization)`，这时候只能在函数返回一个未命名变量的时候进行优化。
|
||||
|
||||
后来更进一步，可以在函数返回命名变量的时候也进行优化了，这就是 `NRVO(named return value optimization)`。
|
||||
|
||||
但是这时候，还有一种情况不能优化的情况是：如果 `createA`函数内部不同的分支返回不同的对象。
|
||||
|
||||
```
|
||||
A createA(int a)
|
||||
{
|
||||
if(a%2==0)
|
||||
{
|
||||
A tmp;
|
||||
tmp._a = 2;
|
||||
return tmp;
|
||||
}
|
||||
else
|
||||
{
|
||||
A tmp;
|
||||
tmp._a = 1;
|
||||
return tmp;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
比如上面这段代码，我在 `gcc 3.4.5` 的情况下测试，发现这种情况是不能优化的。
|
||||
|
||||
但是也不排除 `gcc` 更高的版本或者某些在这方面做得更优秀的编译器已经可以优化这种情况。
|
||||
|
||||
### 3. 隐式类型转换
|
||||
|
||||
代码中的一些类型的隐式转换也会产生临时变量，比如：
|
||||
|
||||
```
|
||||
class A
|
||||
{
|
||||
public:
|
||||
A(int a=0):_a(a)
|
||||
{
|
||||
cout<<"constructor"<<endl;
|
||||
}
|
||||
A(const A &a)
|
||||
{
|
||||
cout<<"copy constructor"<<endl;
|
||||
this->_a = a._a;
|
||||
}
|
||||
A& operator=(const A&a)
|
||||
{
|
||||
cout<<"operator="<<endl;
|
||||
this->_a = a._a;
|
||||
return *this;
|
||||
}
|
||||
int _a;
|
||||
};
|
||||
int main()
|
||||
{
|
||||
A a1;
|
||||
a1 = 3;
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
在 a1 = 3 执行时会首先调用 `A(3)` 产生一个临时对象，然后调用`operator=(const A& a)`。
|
||||
|
||||
这种情况下，我们只要实现一个`A::operator=(int)`函数就可以避免这个临时对象的产生了。
|
||||
|
||||
当然，这只是一个最简单的例子，不过思路是差不多的。
|
||||
|
||||
### 4. 多余的拷贝
|
||||
|
||||
这种情况应该比较少，也比较简单，个人感觉，这种情况主要是疏忽引起的。
|
||||
|
||||
是这样一种情况：
|
||||
|
||||
有个线程级的结构体`thread_data_t *pthread_data`，里面包含请求包的各种数据，在几处使用的使用使用了`const A a = pthread_data->getA()`。
|
||||
|
||||
`getA()`的实现简单来说是返回了`thread_data_t`内部的A的成员。
|
||||
|
||||
因为在一次请求的处理过程中`thread_data_t`内部的 A 的成员不会改变，调用者用`const A a`来接收这个对象就表明调用者也不会改变返回的 A 成员。
|
||||
|
||||
因此，其实完全可以让`getA()`返回A成员的引用，调用者同样用引用来接收：`const A & a = pthread_data->getA()`。
|
||||
|
||||
这样就完全就避免了一次多余的拷贝。
|
||||
|
||||
## 非临时变量
|
||||
|
||||
遇到的一些非临时变量情况有：`stl vector` 的增长引起拷贝构造、`vector` 的赋值、`std::sort` 操作
|
||||
|
||||
### 1. vector的增长
|
||||
|
||||
先简单介绍一下`vector`的增长机制：每次`push_back`时，如果发现原来`vector`的空间用完，会把`vector`调整到原来的 2 倍（ sgi 的实现，`visual studio` 的实现好像是 1.5 倍）。因为 `vector` 空间是连续存储的，这里就有一个问题，如果原来 `vector` 地址后面空余的空间没有被使用，那么`vector`继续把后面的地址申请来就可以扩展其空间了。但是如果后面的空间不够了呢？那就要重新申请一个`2*current_size`大小的空间，然后把`vector`当前，也就是`current_size`的内容拷贝到刚申请的那块空间中去，这时就引起了对象的拷贝操作了。
|
||||
|
||||
假设`vector`初始大小是 0，我们通过`push_back`加入了 10 个对象，以`sgi`实现的两倍增长为例，再假设每次调整`vector`空间的时候都需要调整地址，一共引入了多少次无用的拷贝？
|
||||
|
||||
因为`vector`空间是`1->2->4->8->16`增长的，拷贝的次数一共是四次，每次拷贝对象分别是`1、2、4、8`个。所以答案是`1+2+4+8=15`。
|
||||
|
||||
很容易看出规律，拷贝对象的个数等于最终`vector`空间大小减一。
|
||||
|
||||
那么如果`vector`大小最终会涨到 1000，1W 呢？数据就很可观了。
|
||||
|
||||
我接触过好几个服务，最终`vector`可能会增长到 10W 左右的。如果`vector`要放入 10W 个元素，那么就会开辟`131072`的空间，也就是说最多会引入 13W 次的对象拷贝，而这个拷贝操作是无效的、是可以避免的。
|
||||
|
||||
其实要避免`vector`增长引入的拷贝也很简单，在`push_back`之前先调用`reserve`申请一个估算的最大空间。
|
||||
|
||||
比如我们之前优化的一些服务，预期`vector`最大可能会增长到 10W，那么直接调用`v.reserve(100000)`就可以了。
|
||||
|
||||
当然，这也许会引起一些内存使用的浪费，这就需要使用时注意权衡了。
|
||||
|
||||
但如果你的服务是一直运行的，而且这个`vecto`r对象也是常驻内存的，个人觉得完全可以`reserve`一个最大的空间。因为`vector`空间增长之后，就算调用`clear`清除所有元素，内存也是不会释放的。除非使用和空`vector`交换的方式强制释放它的内存。
|
||||
|
||||
### 2. vector的赋值
|
||||
|
||||
遇到过这样一种情况，在一个函数接受一个`vector &`作为输入，经过一系列处理得到一个临时的`vector`，并在函数返回前将这个临时的`vector`赋值给作为参数的`vector &`作为返回值。简化一下代码如下：
|
||||
|
||||
```
|
||||
void cal_result(vector<int> &input_ret)
|
||||
{
|
||||
vector<int> tmp;
|
||||
for(...)
|
||||
{
|
||||
... // input_ret will be used
|
||||
//fill tmp
|
||||
}
|
||||
input_ret = tmp;
|
||||
}
|
||||
```
|
||||
|
||||
这里，我们可以注意到函数返回后 `tmp` 对象也就消失了，不会被继续使用，所以如果可以的话，我们根本不需要返回 `tmp`的拷贝，直接返回 `tmp` 占用的空间就可以了。
|
||||
|
||||
那么怎么可以直接返回 `tmp` 而不引起拷贝呢？是不是可以这样想，我们把 `tmp`这个`vector`指向的地址赋值给`input_ret`，把`tmp`指向的空间和大小设置为 0 就可以了？
|
||||
|
||||
那么我们完全可以使用`vector`的`swap`操作。它只是将两个`vector`指向空间等等信息交换了一下，而不会引起元素的拷贝，它的操作是常数级的，和交互对象中元素数目无关。
|
||||
|
||||
因此将上述代码改为：
|
||||
|
||||
```
|
||||
void cal_result(vector<int> &input_ret)
|
||||
{
|
||||
vector<int> tmp;
|
||||
for(...)
|
||||
{
|
||||
... // input_ret will be used
|
||||
//fill tmp
|
||||
}
|
||||
input_ret.swap(tmp);
|
||||
}
|
||||
```
|
||||
|
||||
可以减少`tmp`元素的拷贝操作，大大提高了该函数的处理效率。（提高多少，要看`tmp`中所有元素拷贝的代价多大）
|
||||
|
||||
### 3. std::sort操作
|
||||
|
||||
在为一个模块做性能优化的时候，发现一个`vector`的`sort`的操作十分消耗性能，占了整个模块消耗`CPU 10%`以上。
|
||||
|
||||
使用`gperftools`的`cpu profiler`分析了一下数据，发现`sort`操作调用了元素的拷贝构造和赋值函数，这才是消耗性能的原因。
|
||||
|
||||
进一步分析，`vector`中的元素对象特别庞大，对象中又嵌套了其他对象且嵌套了好几层，因此函数的拷贝和赋值的操作代价会比较大。
|
||||
|
||||
而`std::sort`采用的是内省排序+插入排序的方式（ sgi 的实现），不可避免地会引入对象的交换和移动。（其实不管怎么排序都避免不了交换和移动的吧...）
|
||||
|
||||
因此，要优化这句`std::sort`操作，还需要减少对象交换或者提高交换的效率上入手。
|
||||
|
||||
1. 减少对象的交换
|
||||
|
||||
我们采用的减少对象交换的方式是：先使用`index`的方式进行排序，排序好了之后，把原来的`vector`中的对象按照`index`排序的结果最终做一次拷贝，拷贝到这个对象排序后应该在的位置。
|
||||
|
||||
1. 提高交换的效率
|
||||
|
||||
如果对象的实现是如下这样的：
|
||||
|
||||
```
|
||||
class A
|
||||
{
|
||||
public:
|
||||
A(const char* src)
|
||||
{
|
||||
_len = strlen(src);
|
||||
_content = new char[_len];
|
||||
memcpy(_content,src,_len);
|
||||
}
|
||||
A(const A &a)
|
||||
{
|
||||
*this = a;
|
||||
}
|
||||
A& operator=(const A&a)
|
||||
{
|
||||
_len = a._len;
|
||||
_content = new char[_len];
|
||||
memcpy(_content,src,_len);
|
||||
}
|
||||
private:
|
||||
char *_content;
|
||||
int _len;
|
||||
};
|
||||
```
|
||||
|
||||
这里为了保持代码简短，省略了部分实现且没考虑一些安全性的校验。
|
||||
|
||||
那么在对象交换的时候，其实是没有必要调用拷贝构造函数和赋值函数的（`std::swap`的默认实现），直接交换两个对象的`_content`和`_len`值就好了。如果调用拷贝构造函数和赋值函数的话，不可避免还要引入`new、memcpy、strlen、delete`等等操作。
|
||||
|
||||
这种情况下，我们完全可以针对 A 的实现，重载全局的`swap`操作。这样`sort`的过程中就可以调用我们自己实现的高效的`swap`了。
|
||||
|
||||
如下代码可以重载我们 A 函数的`swap`实现：
|
||||
|
||||
```
|
||||
namespace std
|
||||
{
|
||||
template<>
|
||||
void swap<A>(A &a1,A& a2)
|
||||
{
|
||||
cout<<"swap A"<<endl;
|
||||
int tmp = a1._a;
|
||||
a1._a = a2._a;
|
||||
a2._a = tmp;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
因为调用堆精度问题和编译优化的问题，有时候也可能分析不到 `sort` 是因为调用了元素对象的拷贝构造和赋值函数所以才效率比较低。所以发现`sort`消耗性能的时候，可以看看是否是因为`sort`对象过大造成的，积累一个`common sense`吧。
|
||||
2114
source/_posts/c++/base/memory/Cplusplus内存管理.md
Normal file
2114
source/_posts/c++/base/memory/Cplusplus内存管理.md
Normal file
File diff suppressed because it is too large
Load Diff
447
source/_posts/c++/base/memory/一起探索Cplusplus类内存分布.md
Normal file
447
source/_posts/c++/base/memory/一起探索Cplusplus类内存分布.md
Normal file
@ -0,0 +1,447 @@
|
||||
---
|
||||
title: 一起探索Cplusplus类内存分布
|
||||
tag:
|
||||
- memory
|
||||
- c++
|
||||
categories:
|
||||
- c++
|
||||
abbrlink: 97623f3c
|
||||
---
|
||||
|
||||
# 一起探索Cplusplus类内存分布
|
||||
C++ 类中内存分布具体是怎么样，尤其是C++中含有继承、虚函数、虚拟继承以及菱形继承等等情况下。
|
||||
|
||||
由于在`linux`下没有`windows`下显示直观，我们采用`vs2015`进行调试。
|
||||
|
||||
------
|
||||
|
||||
- **部署环境**
|
||||
|
||||
我们在 `属性->C/C++ ->命令行 -> /d1 reportSingleClassLayoutXXX` ,XXX表示类名；
|
||||
|
||||
|
||||
|
||||
------
|
||||
|
||||
- **单个基础类**
|
||||
|
||||
```
|
||||
class Base
|
||||
{
|
||||
private:
|
||||
int a;
|
||||
int b;
|
||||
public:
|
||||
void test();
|
||||
};
|
||||
```
|
||||
|
||||
内存分布：
|
||||
|
||||
```
|
||||
class Base size(8):
|
||||
+-- -
|
||||
0 | a
|
||||
4 | b
|
||||
+-- -
|
||||
```
|
||||
|
||||
**总结**：我们发现普通类的内存分布是根据声明的顺序进行的,成员函数不占用内存。
|
||||
|
||||
------
|
||||
|
||||
- **基础类+继承类**
|
||||
|
||||
```
|
||||
class Base
|
||||
{
|
||||
int a;
|
||||
int b;
|
||||
public:
|
||||
void test();
|
||||
};
|
||||
|
||||
class Divide :public Base
|
||||
{
|
||||
public:
|
||||
void run();
|
||||
private:
|
||||
int c;
|
||||
int d;
|
||||
};
|
||||
```
|
||||
|
||||
内存分布：
|
||||
|
||||
```
|
||||
class Divide size(16) :
|
||||
+-- -
|
||||
0 | +-- - (base class Base)
|
||||
0 | | a
|
||||
4 | | b
|
||||
| +-- -
|
||||
8 | c
|
||||
12 | d
|
||||
+-- -
|
||||
```
|
||||
|
||||
**总结**：根据内存分布，我们发现普通继承类，内存分布也是按照声明的顺序进行的，成员函数不占用内存；类的顺序是先基类，后子类。
|
||||
|
||||
------
|
||||
|
||||
- **含有虚函数的基类**
|
||||
|
||||
```
|
||||
class Base
|
||||
{
|
||||
int a;
|
||||
int b;
|
||||
public:
|
||||
void test();
|
||||
virtual void run();
|
||||
};
|
||||
```
|
||||
|
||||
内存分布：
|
||||
|
||||
```
|
||||
class Base size(12) :
|
||||
+-- -
|
||||
0 | {vfptr}
|
||||
4 | a
|
||||
8 | b
|
||||
+-- -
|
||||
|
||||
Base::$vftable@:
|
||||
| &Base_meta
|
||||
| 0
|
||||
0 | &Base::run
|
||||
```
|
||||
|
||||
**总结**：带有虚函数的内存分布分为两部分，一部分是内存分布，一部分是虚表；我们从最上面发现，`vfptr`是放在了内存开始处，然后才是成员变量；虚函数`run`前面表示这个虚函数的序号为`0`。
|
||||
|
||||
------
|
||||
|
||||
- **含有虚函数的基类+继承子类**
|
||||
|
||||
```
|
||||
class Base
|
||||
{
|
||||
int a;
|
||||
int b;
|
||||
public:
|
||||
void test();
|
||||
virtual void run();
|
||||
};
|
||||
|
||||
class Divide :public Base
|
||||
{
|
||||
public:
|
||||
void DivideFun();
|
||||
virtual void run();
|
||||
private:
|
||||
int c;
|
||||
int d;
|
||||
};
|
||||
```
|
||||
|
||||
内存分布：
|
||||
|
||||
```
|
||||
class Divide size(20) :
|
||||
+-- -
|
||||
0 | +-- - (base class Base)
|
||||
0 | | {vfptr}
|
||||
4 | | a
|
||||
8 | | b
|
||||
| +-- -
|
||||
12 | c
|
||||
16 | d
|
||||
+-- -
|
||||
|
||||
Divide::$vftable@:
|
||||
| &Divide_meta
|
||||
| 0
|
||||
0 | &Divide::run
|
||||
```
|
||||
|
||||
**总结**：我们发现继承类，虚表只有一个，还是在内存开始处，内存排布顺序与普通继承类是一致的；
|
||||
|
||||
------
|
||||
|
||||
- **含有虚函数的基类+继承子类（多增加一个虚函数）**
|
||||
|
||||
```
|
||||
class Base
|
||||
{
|
||||
int a;
|
||||
int b;
|
||||
public:
|
||||
void test();
|
||||
virtual void run();
|
||||
};
|
||||
|
||||
class Divide :public Base
|
||||
{
|
||||
public:
|
||||
void DivideFun();
|
||||
virtual void run();
|
||||
virtual void DivideRun();
|
||||
private:
|
||||
int c;
|
||||
int d;
|
||||
};
|
||||
```
|
||||
|
||||
内存分布：
|
||||
|
||||
```
|
||||
class Divide size(20) :
|
||||
+-- -
|
||||
0 | +-- - (base class Base)
|
||||
0 | | {vfptr}
|
||||
4 | | a
|
||||
8 | | b
|
||||
| +-- -
|
||||
12 | c
|
||||
16 | d
|
||||
+-- -
|
||||
|
||||
Divide::$vftable@:
|
||||
| &Divide_meta
|
||||
| 0
|
||||
0 | &Divide::run
|
||||
1 | &Divide::DivideRun
|
||||
```
|
||||
|
||||
**总结**：虚表还是继承于基类，在虚表部分多了`DivideRun`序号为`1`的虚函数；
|
||||
|
||||
------
|
||||
|
||||
- **多重继承**
|
||||
|
||||
```
|
||||
class Base
|
||||
{
|
||||
int a;
|
||||
int b;
|
||||
public:
|
||||
virtual void run();
|
||||
};
|
||||
|
||||
class Divide1 :public Base
|
||||
{
|
||||
public:
|
||||
virtual void run();
|
||||
private:
|
||||
int c;
|
||||
};
|
||||
|
||||
class Divide2 :public Base
|
||||
{
|
||||
public:
|
||||
virtual void run();
|
||||
private:
|
||||
int d;
|
||||
};
|
||||
|
||||
class Divide :public Divide1, Divide2
|
||||
{
|
||||
public:
|
||||
virtual void run();
|
||||
private:
|
||||
int d;
|
||||
};
|
||||
```
|
||||
|
||||
内存分布：
|
||||
|
||||
```
|
||||
class Divide1 size(16) :
|
||||
+-- -
|
||||
0 | +-- - (base class Base)
|
||||
0 | | {vfptr}
|
||||
4 | | a
|
||||
8 | | b
|
||||
| +-- -
|
||||
12 | c
|
||||
+-- -
|
||||
|
||||
Divide1::$vftable@:
|
||||
| &Divide1_meta
|
||||
| 0
|
||||
0 | &Divide1::run
|
||||
|
||||
Divide1::run this adjustor: 0
|
||||
|
||||
class Divide2 size(16) :
|
||||
+-- -
|
||||
0 | +-- - (base class Base)
|
||||
0 | | {vfptr}
|
||||
4 | | a
|
||||
8 | | b
|
||||
| +-- -
|
||||
12 | d
|
||||
+-- -
|
||||
|
||||
Divide2::$vftable@:
|
||||
| &Divide2_meta
|
||||
| 0
|
||||
0 | &Divide2::run
|
||||
|
||||
Divide2::run this adjustor: 0
|
||||
|
||||
class Divide size(36) :
|
||||
+-- -
|
||||
0 | +-- - (base class Divide1)
|
||||
0 | | +-- - (base class Base)
|
||||
0 | | | {vfptr}
|
||||
4 | | | a
|
||||
8 | | | b
|
||||
| | +-- -
|
||||
12 | | c
|
||||
| +-- -
|
||||
| +-- - (base class Divide2)
|
||||
| | +-- - (base class Base)
|
||||
| | | {vfptr}
|
||||
| | | a
|
||||
| | | b
|
||||
| | +-- -
|
||||
| | d
|
||||
| +-- -
|
||||
| d
|
||||
+-- -
|
||||
|
||||
Divide::$vftable@Divide1@:
|
||||
| &Divide_meta
|
||||
| 0
|
||||
0 | &Divide::run
|
||||
|
||||
Divide::$vftable@Divide2@:
|
||||
| -16
|
||||
0 | &thunk: this -= 16; goto Divide::run
|
||||
|
||||
Divide::run this adjustor: 0
|
||||
```
|
||||
|
||||
总结：主要看最后一个`Divide`类，内存排列顺序先是Divide1，后是Divide2，在Divide1和Divide2中各有一份虚表；
|
||||
|
||||
------
|
||||
|
||||
- **虚拟继承（菱形继承）**
|
||||
|
||||
```
|
||||
class Base
|
||||
{
|
||||
int a;
|
||||
int b;
|
||||
public:
|
||||
virtual void run();
|
||||
};
|
||||
|
||||
class Divide1 :virtual public Base
|
||||
{
|
||||
public:
|
||||
virtual void run();
|
||||
private:
|
||||
int c;
|
||||
};
|
||||
|
||||
class Divide2 :virtual public Base
|
||||
{
|
||||
public:
|
||||
virtual void run();
|
||||
private:
|
||||
int d;
|
||||
};
|
||||
|
||||
class Divide :public Divide1, Divide2
|
||||
{
|
||||
public:
|
||||
virtual void run();
|
||||
private:
|
||||
int d;
|
||||
};
|
||||
```
|
||||
|
||||
**内存分布：**
|
||||
|
||||
```
|
||||
class Divide1 size(20) :
|
||||
+-- -
|
||||
0 | {vbptr}
|
||||
4 | c
|
||||
+-- -
|
||||
+-- - (virtual base Base)
|
||||
8 | {vfptr}
|
||||
12 | a
|
||||
16 | b
|
||||
+-- -
|
||||
|
||||
Divide1::$vbtable@:
|
||||
0 | 0
|
||||
1 | 8 (Divide1d(Divide1 + 0)Base)
|
||||
|
||||
Divide1::$vftable@:
|
||||
| -8
|
||||
0 | &Divide1::run
|
||||
|
||||
Divide1::run this adjustor: 8
|
||||
vbi: class offset o.vbptr o.vbte fVtorDisp
|
||||
Base 8 0 4 0
|
||||
|
||||
class Divide2 size(20) :
|
||||
+-- -
|
||||
0 | {vbptr}
|
||||
4 | d
|
||||
+-- -
|
||||
+-- - (virtual base Base)
|
||||
8 | {vfptr}
|
||||
12 | a
|
||||
16 | b
|
||||
+-- -
|
||||
|
||||
Divide2::$vbtable@:
|
||||
0 | 0
|
||||
1 | 8 (Divide2d(Divide2 + 0)Base)
|
||||
|
||||
Divide2::$vftable@:
|
||||
| -8
|
||||
0 | &Divide2::run
|
||||
|
||||
Divide2::run this adjustor: 8
|
||||
vbi: class offset o.vbptr o.vbte fVtorDisp
|
||||
Base 8 0 4 0
|
||||
|
||||
class Divide size(32) :
|
||||
+-- -
|
||||
0 | +-- - (base class Divide1)
|
||||
0 | | {vbptr}
|
||||
4 | | c
|
||||
| +-- -
|
||||
8 | +-- - (base class Divide2)
|
||||
8 | | {vbptr}
|
||||
12 | | d
|
||||
| +-- -
|
||||
16 | d
|
||||
+-- -
|
||||
+-- - (virtual base Base)
|
||||
20 | {vfptr}
|
||||
24 | a
|
||||
28 | b
|
||||
+-- -
|
||||
|
||||
Divide::$vbtable@Divide1@:
|
||||
0 | 0
|
||||
1 | 20 (Divided(Divide1 + 0)Base)
|
||||
|
||||
Divide::$vbtable@Divide2@:
|
||||
0 | 0
|
||||
1 | 12 (Divided(Divide2 + 0)Base)
|
||||
|
||||
Divide::$vftable@:
|
||||
| -20
|
||||
0 | &Divide::run
|
||||
```
|
||||
|
||||
总结：通过内存分布可知，`Divide1`和`Divide2`都是两个虚表，Divide中却是成了3个虚表，只有一份base；所以说：**虚继承的作用是减少了对基类的重复，代价是增加了虚表指针的负担（增加了更多的需指针）**
|
||||
BIN
source/_posts/c++/base/memory/一起探索Cplusplus类内存分布/images/640.png
Normal file
BIN
source/_posts/c++/base/memory/一起探索Cplusplus类内存分布/images/640.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 72 KiB |
425
source/_posts/c++/base/point/C语言中三块难啃的硬骨头.md
Normal file
425
source/_posts/c++/base/point/C语言中三块难啃的硬骨头.md
Normal file
@ -0,0 +1,425 @@
|
||||
---
|
||||
abbrlink: '0'
|
||||
---
|
||||
# [C语言中三块难啃的硬骨头](https://mp.weixin.qq.com/s/Ntr0cw7zeLNZbd-kdnjMsQ)
|
||||
|
||||
C语言在嵌入式学习中是必备的知识，审核大部分操作都要围绕C语言进行，而其中有三块“难啃的硬骨头”几乎是公认级别的。
|
||||
|
||||
|
||||
|
||||
# 0x01 指针
|
||||
|
||||
指针公认最难理解的概念，也是让很多初学者选择放弃的直接原因。
|
||||
|
||||
指针之所以难理解，因为指针本身就是一个变量，是一个非常特殊的变量，专门存放地址的变量，这个地址需要给申请空间才能装东西，而且因为是个变量可以中间赋值，这么一倒腾很多人就开始犯晕了，绕不开弯了。C语言之所以被很多高手所喜欢，就是指针的魅力，中间可以灵活的切换，执行效率超高，这点也是让小白晕菜的地方。
|
||||
|
||||
指针是学习绕不过去的知识点，而且学完C语言，下一步紧接着切换到数据结构和算法，指针是切换的重点，指针搞不定下一步进行起来就很难，会让很多人放弃继续学习的勇气。
|
||||
|
||||
指针直接对接内存结构，常见的C语言里面的指针乱指，数组越界根本原因就是内存问题。在指针这个点有无穷无尽的发挥空间。很多编程的技巧都在此集结。
|
||||
|
||||
指针还涉及如何申请释放内存，如果释放不及时就会出现内存泄露的情况，指针是高效好用，但不彻底搞明白对于有些人来说简直就是噩梦。
|
||||
|
||||
在概念方面问题可以参见此前推文《对于C语言指针最详尽的讲解》，那么在指针方面可以参见一下大神的经验：
|
||||
|
||||
## **复杂类型说明**
|
||||
|
||||
要了解指针，多多少少会出现一些比较复杂的类型。所以先介绍一下如何完全理解一个复杂类型。
|
||||
|
||||
要理解复杂类型其实很简单，一个类型里会出现很多运算符，他们也像普通的表达式一样，有优先级，其优先级和运算优先级一样。
|
||||
|
||||
所以笔者总结了一下其原则：从变量名处起，根据运算符优先级结合，一步一步分析。
|
||||
|
||||
下面让我们先从简单的类型开始慢慢分析吧。
|
||||
|
||||
```
|
||||
int p;
|
||||
```
|
||||
|
||||
这是一个普通的整型变量
|
||||
|
||||
```
|
||||
int p;
|
||||
```
|
||||
|
||||
首先从P处开始，先与结合，所以说明P是一个指针。然后再与int结合，说明指针所指向的内容的类型为int型，所以P是一个返回整型数据的指针
|
||||
|
||||
```
|
||||
int p[3];
|
||||
```
|
||||
|
||||
首先从P处开始，先与[]结合，说明P是一个数组。然后与int结合，说明数组里的元素是整型的，所以P是一个由整型数据组成的数组。
|
||||
|
||||
```
|
||||
int *p[3];
|
||||
```
|
||||
|
||||
首先从P处开始，先与[]结合，因为其优先级比高，所以P是一个数组。然后再与结合，说明数组里的元素是指针类型。之后再与int结合，说明指针所指向的内容的类型是整型的，所以P是一个由返回整型数据的指针所组成的数组。
|
||||
|
||||
```
|
||||
int (*p)[3];
|
||||
```
|
||||
|
||||
首先从P处开始，先与结合，说明P是一个指针。然后再与[]结合(与"()"这步可以忽略，只是为了改变优先级)，说明指针所指向的内容是一个数组。之后再与int结合，说明数组里的元素是整型的。所以P是一个指向由整型数据组成3个整数的指针。
|
||||
|
||||
```
|
||||
int **p;
|
||||
```
|
||||
|
||||
首先从P开始，先与*结合，说明P是一个指针。然后再与*结合，说明指针所指向的元素是指针。之后再与int结合，说明该指针所指向的元素是整型数据。由于二级指针以及更高级的指针极少用在复杂的类型中，所以后面更复杂的类型我们就不考虑多级指针了，最多只考虑一级指针。
|
||||
|
||||
```
|
||||
int p(int);
|
||||
```
|
||||
|
||||
从P处起，先与()结合，说明P是一个函数。然后进入()里分析，说明该函数有一个整型变量的参数，之后再与外面的int结合，说明函数的返回值是一个整型数据。
|
||||
|
||||
```
|
||||
int (*p)(int);
|
||||
```
|
||||
|
||||
从P处开始，先与指针结合，说明P是一个指针。然后与()结合，说明指针指向的是一个函数。之后再与()里的int结合，说明函数有一个int型的参数，再与最外层的int结合，说明函数的返回类型是整型，所以P是一个指向有一个整型参数且返回类型为整型的函数的指针。
|
||||
|
||||
```
|
||||
int (p(int))[3];
|
||||
```
|
||||
|
||||
可以先跳过，不看这个类型，过于复杂。从P开始，先与()结合，说明P是一个函数。然后进入()里面，与int结合，说明函数有一个整型变量参数。然后再与外面的结合，说明函数返回的是一个指针。之后到最外面一层，先与[]结合，说明返回的指针指向的是一个数组。接着再与结合，说明数组里的元素是指针，最后再与int结合，说明指针指向的内容是整型数据。所以P是一个参数为一个整数据且返回一个指向由整型指针变量组成的数组的指针变量的函数。
|
||||
|
||||
说到这里也就差不多了。理解了这几个类型，其它的类型对我们来说也是小菜了。不过一般不会用太复杂的类型，那样会大大减小程序的可读性，请慎用。这上面的几种类型已经足够我们用了。
|
||||
|
||||
## **细说指针**
|
||||
|
||||
指针是一个特殊的变量，它里面存储的数值被解释成为内存里的一个地址。
|
||||
|
||||
要搞清一个指针需要搞清指针的四方面的内容：指针的类型、指针所指向的类型、指针的值或者叫指针所指向的内存区、指针本身所占据的内存区。让我们分别说明。
|
||||
|
||||
先声明几个指针放着做例子：
|
||||
|
||||
```
|
||||
（1）int*ptr;
|
||||
|
||||
（2）char*ptr;
|
||||
|
||||
（3）int**ptr;
|
||||
|
||||
（4）int(*ptr)[3];
|
||||
|
||||
（5）int*(*ptr)[4];
|
||||
```
|
||||
|
||||
## **指针的类型**
|
||||
|
||||
从语法的角度看，小伙伴们只要把指针声明语句里的指针名字去掉，剩下的部分就是这个指针的类型。这是指针本身所具有的类型。
|
||||
|
||||
让我们看看上述例子中各个指针的类型：
|
||||
|
||||
```
|
||||
（1）intptr;//指针的类型是int
|
||||
|
||||
（2）charptr;//指针的类型是char
|
||||
|
||||
（3）intptr;//指针的类型是int
|
||||
|
||||
（4）int(ptr)[3];//指针的类型是int()[3]
|
||||
|
||||
（5）int*(ptr)[4];//指针的类型是int(*)[4]
|
||||
```
|
||||
|
||||
怎么样？找出指针的类型的方法是不是很简单？
|
||||
|
||||
## **指针所指向的类型**
|
||||
|
||||
当通过指针来访问指针所指向的内存区时，指针所指向的类型决定了编译器将把那片内存区里的内容当做什么来看待。
|
||||
|
||||
从语法上看，小伙伴们只需把指针声明语句中的指针名字和名字左边的指针声明符*去掉，剩下的就是指针所指向的类型。
|
||||
|
||||
上述例子中各个指针所指向的类型：
|
||||
|
||||
```
|
||||
（1）intptr; //指针所指向的类型是int
|
||||
|
||||
（2）char*ptr; //指针所指向的的类型是char*
|
||||
|
||||
（3）int*ptr; //指针所指向的的类型是int*
|
||||
|
||||
（4）int(*ptr)[3]; //指针所指向的的类型是int(*)[3]
|
||||
|
||||
（5）int*(*ptr)[4]; //指针所指向的的类型是int*(*)[4]
|
||||
```
|
||||
|
||||
在指针的算术运算中，指针所指向的类型有很大的作用。
|
||||
|
||||
指针的类型(即指针本身的类型)和指针所指向的类型是两个概念。当小伙伴们对C 越来越熟悉时，就会发现，把与指针搅和在一起的"类型"这个概念分成"指针的类型"和"指针所指向的类型"两个概念，是精通指针的关键点之一。
|
||||
|
||||
笔者看了不少书，发现有些写得差的书中，就把指针的这两个概念搅在一起了，所以看起书来前后矛盾，越看越糊涂。
|
||||
|
||||
## **指针的值**
|
||||
|
||||
即指针所指向的内存区或地址。
|
||||
|
||||
指针的值是指针本身存储的数值，这个值将被编译器当作一个地址，而不是一个一般的数值。
|
||||
|
||||
在32位程序里，所有类型的指针的值都是一个32位整数，因为32位程序里内存地址全都是32位长。指针所指向的内存区就是从指针的值所代表的那个内存地址开始，长度为si zeof(指针所指向的类型)的一片内存区。
|
||||
|
||||
以后，我们说一个指针的值是XX，就相当于说该指针指向了以XX为首地址的一片内存区域；我们说一个指针指向了某块内存区域，就相当于说该指针的值是这块内存区域的首地址。
|
||||
|
||||
指针所指向的内存区和指针所指向的类型是两个完全不同的概念。在例一中，指针所指向的类型已经有了，但由于指针还未初始化，所以它所指向的内存区是不存在的，或者说是无意义的。
|
||||
|
||||
以后，每遇到一个指针，都应该问问：这个指针的类型是什么？指针指的类型是什么？该指针指向了哪里？
|
||||
|
||||
## **指针本身所占据的内存区**
|
||||
|
||||
指针本身占了多大的内存？只要用函数sizeof(指针的类型)测一下就知道了。在32位平台里，指针本身占据4个字节的长度。指针本身占据的内存这个概念在判断一个指针表达式是否是左值时很有用。
|
||||
|
||||
# 0x02 函数
|
||||
|
||||
面向过程对象模块的基本单位，以及对应各种组合，函数指针，指针函数
|
||||
|
||||
一个函数就是一个业务逻辑块，是面向过程，单元模块的最小单元，而且在函数的执行过程中，形参，实参如何交换数据，如何将数据传递出去，如何设计一个合理的函数，不单单是解决一个功能，还要看是不是能够复用，避免重复造轮子。
|
||||
|
||||
函数指针和指针函数，表面是两个字面意思的互换实际上含义截然不同，指针函数比较好理解，就是返回指针的一个函数，函数指针这个主要用在回调函数，很多人觉得函数都没还搞明白，回调函数更晕菜了。其实可以通俗的理解指向函数的指针，本身是一个指针变量，只不过在初始化的时候指向了函数，这又回到了指针层面。没搞明白指针再次深入的向前走特别难。
|
||||
|
||||
|
||||
|
||||
C语言的开发者们为后来的开发者做了一些省力气的事情，他们编写了大量代码，将常见的基本功能都完成了，可以让别人直接拿来使用。但是那么多代码，如何从中找到自己需要的呢？将所有代码都拿来显然是不太现实。
|
||||
|
||||
但是这些代码，早已被早期的开发者们分门别类地放在了不同的文件中，并且每一段代码都有唯一的名字。所以其实学习C语言并没有那么难，尤其是可以在动手锻炼做项目中进行。使用代码时，只要在对应的名字后面加上( )就可以。这样的一段代码就是函数，函数能够独立地完成某个功能，一次编写完成后可以多次使用。
|
||||
|
||||
很多初学者可能都会把C语言中的函数和数学中的函数概念搞混淆。其实真相并没有那么复杂，C语言中的函数是有规律可循迹的，只要搞清楚了概念你会发现还挺有意思的。函数的英文名称是 Function，对应翻译过来的中文还有“功能”的意思。C语言中的函数也跟功能有着密切的关系。
|
||||
|
||||
我们来看一小段C语言代码：
|
||||
|
||||
```
|
||||
#include<stdio.h>
|
||||
int main()
|
||||
{
|
||||
puts("Hello World");
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
把目光放在第4行代码上，这行代码会在显示器上输出“Hello World”。前面我们已经讲过，puts 后面要带()，字符串也要放在()中。
|
||||
|
||||
在C语言中，有的语句使用时不能带括号，有的语句必须带括号。带括号的就是函数（Function）。
|
||||
|
||||
C语言提供了很多功能，我们只需要一句简单的代码就能够使用。但是这些功能的底层都比较复杂，通常是软件和硬件的结合，还要要考虑很多细节和边界，如果将这些功能都交给程序员去完成，那将极大增加程序员的学习成本，降低编程效率。
|
||||
|
||||
有了函数之后，C语言的编程效率就好像有了神器一样，开发者们只需要随时调用就可以了，像进程函数、操作函数、时间日期函数等都可以帮助我们直接实现C语言本身的功能。
|
||||
|
||||
**C语言函数是可以重复使用的**。
|
||||
|
||||
函数的一个明显特征就是使用时必须带括号()，必要的话，括号中还可以包含待处理的数据。例如puts("果果小师弟")就使用了一段具有输出功能的代码，这段代码的名字是 puts，"尚观科技" 是要交给这段代码处理的数据。使用函数在编程中有专业的称呼，叫做函数调用（Function Call）。
|
||||
|
||||
如果函数需要处理多个数据，那么它们之间使用逗号,分隔，例如：
|
||||
|
||||
```
|
||||
pow(10, 2);
|
||||
```
|
||||
|
||||
该函数用来求10的2次方。
|
||||
|
||||
好了，看到这里你有没有觉得其实C语言函数还是比较有意思的，而且并没有那么复杂困难。以后再遇到菜鸟小白的时候，你一口一个C语言的函数，说不定就能当场引来无数膜拜的目光。
|
||||
|
||||
# 0x03 结构体、递归
|
||||
|
||||
很多在大学学习C语言的，很多课程都没学完，结构体都没学到，因为从章节的安排来看好像，结构体学习放在教材的后半部分了，弄得很多学生觉得结构体不重要，如果只是应付学校的考试，或者就是为了混个毕业证，的确学的意义不大。
|
||||
|
||||
如果想从事编程这个行业，对这个概念还不了解，基本上无法构造数据模型，没有一个业务体是完全使用原生数据类型来完成的，很多高手在设计数据模型的时候，一般先把头文件中的结构体数据整理出来。然后设计好功能函数的参数，以及名字，然后才真正开始写c源码。
|
||||
|
||||
如果从节省空间考虑结构体里面的数据放的顺序不一样在内存中占用的空间也不一样，结构体与结构体之间赋值，结构体存在指针那么赋值要特别注意，需要进行深度的赋值。
|
||||
|
||||
递归一般用于从头到位统计或者罗列一些数据，在使用的时候很多初学者都觉得别扭，怎么还能自己调用自己？而且在使用的时候，一定设置好跳出的条件，不然无休止的进行下去，真就成无线死循环了。
|
||||
|
||||
对于结构体方面的知识，可以参见此前推送的文章《C语言结构体（struct）最全的讲解（万字干货）》。具体也可以参见大佬的经验：
|
||||
|
||||
相信大家对于结构体都不陌生。在此，分享出本人对C语言结构体的研究和学习的总结。如果你发现这个总结中有你以前所未掌握的，那本文也算是有点价值了。当然，水平有限，若发现不足之处恳请指出。代码文件test.c我放在下面。在此，我会围绕以下2个问题来分析和应用C语言结构体：
|
||||
|
||||
1. C语言中的结构体有何作用
|
||||
2. 结构体成员变量内存对齐有何讲究(重点)
|
||||
|
||||
对于一些概念的说明，我就不把C语言教材上的定义搬上来。我们坐下来慢慢聊吧。
|
||||
|
||||
## **1. 结构体有何作用**
|
||||
|
||||
三个月前，教研室里一个学长在华为南京研究院的面试中就遇到这个问题。当然，这只是面试中最基础的问题。如果问你你怎么回答？我的理解是这样的，C语言中结构体至少有以下三个作用：
|
||||
|
||||
(1) 有机地组织了对象的属性。
|
||||
|
||||
比如，在STM32的RTC开发中，我们需要数据来表示日期和时间，这些数据通常是年、月、日、时、分、秒。如果我们不用结构体，那么就需要定义6个变量来表示。这样的话程序的数据结构是松散的，我们的数据结构最好是“高内聚，低耦合”的。所以，用一个结构体来表示更好，无论是从程序的可读性还是可移植性还是可维护性皆是：
|
||||
|
||||
```
|
||||
typedef struct //公历日期和时间结构体
|
||||
{
|
||||
vu16 year;
|
||||
vu8 month;
|
||||
vu8 date;
|
||||
vu8 hour;
|
||||
vu8 min;
|
||||
vu8 sec;
|
||||
}_calendar_obj;
|
||||
_calendar_obj calendar; //定义结构体变量
|
||||
```
|
||||
|
||||
(2) 以修改结构体成员变量的方法代替了函数(入口参数)的重新定义。
|
||||
|
||||
如果说结构体有机地组织了对象的属性表示结构体“中看”，那么以修改结构体成员变量的方法代替函数(入口参数)的重新定义就表示了结构体“中用”。继续以上面的结构体为例子，我们来分析。假如现在我有如下函数来显示日期和时间：
|
||||
|
||||
```
|
||||
void DsipDateTime( _calendar_obj DateTimeVal)
|
||||
```
|
||||
|
||||
那么我们只要将一个_calendar_obj这个结构体类型的变量作为实参调用DsipDateTime()即可，DsipDateTime()通过DateTimeVal的成变量来实现内容的显示。如果不用结构体，我们很可能需要写这样的一个函数：
|
||||
|
||||
```
|
||||
void DsipDateTime( vu16 year，vu8 month，vu8 date，vu8 hour，vu8 min，vu8 sec)
|
||||
```
|
||||
|
||||
显然这样的形参很不可观，数据结构管理起来也很繁琐。如果某个函数的返回值得是一个表示日期和时间的数据，那就更复杂了。这只是一方面。
|
||||
|
||||
另一方面，如果用户需要表示日期和时间的数据中还要包含星期(周)，这个时候，如果之前没有用机构体，那么应该在DsipDateTime()函数中在增加一个形参vu8 week：
|
||||
|
||||
```
|
||||
void DsipDateTime( vu16 year，vu8 month，vu8 date，vu8 week，vu8 hour，vu8 min，vu8 sec)
|
||||
```
|
||||
|
||||
可见这种方法来传递参数非常繁琐。所以以结构体作为函数的入口参数的好处之一就是函数的声明void DsipDateTime(_calendar_obj DateTimeVal)不需要改变，只需要增加结构体的成员变量，然后在函数的内部实现上对calendar.week作相应的处理即可。这样，在程序的修改、维护方面作用显著。
|
||||
|
||||
```
|
||||
typedef struct //公历日期和时间结构体
|
||||
{
|
||||
vu16 year;
|
||||
vu8 month;
|
||||
vu8 date;
|
||||
vu8 week;
|
||||
vu8 hour;
|
||||
vu8 min;
|
||||
vu8 sec;
|
||||
}_calendar_obj;
|
||||
_calendar_obj calendar; //定义结构体变量
|
||||
```
|
||||
|
||||
(3) 结构体的内存对齐原则可以提高CPU对内存的访问速度(以空间换取时间)。
|
||||
|
||||
并且，结构体成员变量的地址可以根据基地址(以偏移量offset)计算。我们先来看看下面的一段简单的程序，对于此程序的分析会在第2部分结构体成员变量内存对齐中详细说明。
|
||||
|
||||
```
|
||||
#include<stdio.h>
|
||||
|
||||
int main()
|
||||
{
|
||||
struct //声明结构体char_short_long
|
||||
{
|
||||
char c;
|
||||
short s;
|
||||
long l;
|
||||
}char_short_long;
|
||||
|
||||
struct //声明结构体long_short_char
|
||||
{
|
||||
long l;
|
||||
short s;
|
||||
char c;
|
||||
}long_short_char;
|
||||
|
||||
struct //声明结构体char_long_short
|
||||
{
|
||||
char c;
|
||||
long l;
|
||||
short s;
|
||||
}char_long_short;
|
||||
|
||||
printf(" \n");
|
||||
printf(" Size of char = %d bytes\n",sizeof(char));
|
||||
printf(" Size of shrot = %d bytes\n",sizeof(short));
|
||||
printf(" Size of long = %d bytes\n",sizeof(long));
|
||||
printf(" \n"); //char_short_long
|
||||
printf(" Size of char_short_long = %d bytes\n",sizeof(char_short_long));
|
||||
printf(" Addr of char_short_long.c = 0x%p (10进制：%d)\n",&char_short_long.c,&char_short_long.c);
|
||||
printf(" Addr of char_short_long.s = 0x%p (10进制：%d)\n",&char_short_long.s,&char_short_long.s);
|
||||
printf(" Addr of char_short_long.l = 0x%p (10进制：%d)\n",&char_short_long.l,&char_short_long.l);
|
||||
printf(" \n");
|
||||
|
||||
printf(" \n"); //long_short_char
|
||||
printf(" Size of long_short_char = %d bytes\n",sizeof(long_short_char));
|
||||
printf(" Addr of long_short_char.l = 0x%p (10进制：%d)\n",&long_short_char.l,&long_short_char.l);
|
||||
printf(" Addr of long_short_char.s = 0x%p (10进制：%d)\n",&long_short_char.s,&long_short_char.s);
|
||||
printf(" Addr of long_short_char.c = 0x%p (10进制：%d)\n",&long_short_char.c,&long_short_char.c);
|
||||
printf(" \n");
|
||||
|
||||
printf(" \n"); //char_long_short
|
||||
printf(" Size of char_long_short = %d bytes\n",sizeof(char_long_short));
|
||||
printf(" Addr of char_long_short.c = 0x%p (10进制：%d)\n",&char_long_short.c,&char_long_short.c);
|
||||
printf(" Addr of char_long_short.l = 0x%p (10进制：%d)\n",&char_long_short.l,&char_long_short.l);
|
||||
printf(" Addr of char_long_short.s = 0x%p (10进制：%d)\n",&char_long_short.s,&char_long_short.s);
|
||||
printf(" \n");
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
程序的运行结果如下(注意：括号内的数据是成员变量的地址的十进制形式)：
|
||||
|
||||
|
||||
|
||||
## **2. 结构体成员变量内存对齐**
|
||||
|
||||
首先，我们来分析一下上面程序的运行结果。前三行说明在我的程序中，char型占1个字节，short型占2个字节，long型占4个字节。char_short_long、long_short_char和char_long_short是三个结构体成员相同但是成员变量的排列顺序不同。并且从程序的运行结果来看，
|
||||
|
||||
```
|
||||
Size of char_short_long = 8 bytes
|
||||
Size of long_short_char = 8 bytes
|
||||
Size of char_long_short = 12 bytes //比前两种情况大4 byte ！
|
||||
```
|
||||
|
||||
并且，还要注意到，1 byte (char)+ 2 byte (short)+ 4 byte (long) = 7 byte，而不是8 byte。
|
||||
|
||||
所以，结构体成员变量的放置顺序影响着结构体所占的内存空间的大小。一个结构体变量所占内存的大小不一定等于其成员变量所占空间之和。如果一个用户程序或者操作系统(比如uC/OS-II)中存在大量结构体变量时，这种内存占用必须要进行优化，也就是说，结构体内部成员变量的排列次序是有讲究的。
|
||||
|
||||
结构体成员变量到底是如何存放的呢？
|
||||
|
||||
在这里，我就不卖关子了，直接给出如下结论，在没有#pragma pack宏的情况下：
|
||||
|
||||
- 原则1 结构（struct或联合union）的数据成员，第一个数据成员放在offset为0的地方，以后每个数据成员存储的起始位置要从该成员大小的整数倍开始（比如int在32位机为4字节，则要从4的整数倍地址开始存储）。
|
||||
- 原则2 结构体的总大小，也就是sizeof的结果，必须是其内部最大成员的整数倍，不足的要补齐。
|
||||
- 原则3 结构体作为成员时，结构体成员要从其内部最大元素大小的整数倍地址开始存储。（struct a里存有struct b，b里有char，int，double等元素时，那么b应该从8的整数倍地址处开始存储，因为sizeof(double) = 8 bytes）
|
||||
|
||||
这里，我们结合上面的程序来分析(暂时不讨论原则3)。
|
||||
|
||||
先看看char_short_long和long_short_char这两个结构体，从它们的成员变量的地址可以看出来，这两个结构体符合原则1和原则2。注意，在 char_short_long的成员变量的地址中，char_short_long.s的地址是1244994，也就是说，1244993是“空的”，只是被“占位”了！
|
||||
|
||||
| 成员变量 | 成员变量十六进制地址 | 成员变量十进制地址 |
|
||||
| :---------------- | :------------------- | :----------------- |
|
||||
| char_long_short.c | 0x0012FF2C | 1244972 |
|
||||
| char_long_short.l | 0x0012FF30 | 1244976 |
|
||||
| char_long_short.s | 0x0012FF34 | 1244980 |
|
||||
|
||||
可见，其内存分布图如下，共12 bytes：
|
||||
|
||||
|
||||
|
||||
首先，1244972能被1整除，所以char_long_short.c放在1244972处没有问题(其实，就char型成员变量自身来说，其放在任何地址单元处都没有问题)，根据原则1，在之后的1244973~1244975中都没有能被4(因为sizeof(long)=4bytes)整除的，1244976能被4整除，所以char_long_short.l应该放在1244976处，那么同理，最后一个.s(sizeof(short)=2 bytes)是应该放在1244980处。
|
||||
|
||||
是不是这样就结束了？不是，还有原则2。根据原则2的要求，char_long_short这个结构体所占的空间大小应该是其占内存空间最大的成员变量的大小的整数倍。如果我们到此就结束了，那么char_long_short所占的内存空间是1244972~1244981共计10bytes，不符合原则2，所以，必须在最后补齐2个 bytes(1244982~1244983)。
|
||||
|
||||
至此，一个结构体的内存布局完成了。
|
||||
|
||||
下面我们按照上述原则，来验证这样的分析是不是正确。按上面的分析，地址单元1244973、1244974、1244975以及1244982、1244983都是空的(至少char_long_short未用到，只是“占位”了)。如果我们的分析是正确的，那么，定义这样一个结构体，其所占内存也应该是12 bytes：
|
||||
|
||||
```
|
||||
struct //声明结构体char_long_short_new
|
||||
{
|
||||
char c;
|
||||
char add1; //补齐空间
|
||||
char add2; //补齐空间
|
||||
char add3; //补齐空间
|
||||
long l;
|
||||
short s;
|
||||
char add4; //补齐空间
|
||||
char add5; //补齐空间
|
||||
}char_long_short_new;
|
||||
```
|
||||
|
||||
可见，我们的分析是正确的。至于原则3，大家可以自己编程验证，这里就不再讨论了。
|
||||
|
||||
所以，无论你是在VC6.0还是Keil C51，还是Keil MDK中，当你需要定义一个结构体时，只要你稍微留心结构体成员变量内存对齐这一现象，就可以在很大程度上节约MCU的RAM。这一点不仅仅应用于实际编程，在很多大型公司，比如IBM、微软、百度、华为的笔试和面试中，也是常见的。
|
||||
|
||||
这三大块硬骨头是学习C语言的绊脚石，下功夫拿掉基本上C语言的大动脉就打通了，那么再去学习别的内容就相对比较简单了。编程学习过程中越是痛苦的时候，学到的东西就会越多，克服过去就会自己的技能，放弃了前面的付出的时间都将清零。越是难学的语言在入门之后，在入门之后越觉得过瘾，而且还容易上瘾。你上瘾了没？还是放弃了？
|
||||
BIN
source/_posts/c++/base/point/C语言中三块难啃的硬骨头/images/640.webp
Normal file
BIN
source/_posts/c++/base/point/C语言中三块难啃的硬骨头/images/640.webp
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 62 KiB |
Binary file not shown.
|
After Width: | Height: | Size: 92 KiB |
Binary file not shown.
|
After Width: | Height: | Size: 726 KiB |
285
source/_posts/data_structure/hashmap/HashMap.md
Normal file
285
source/_posts/data_structure/hashmap/HashMap.md
Normal file
@ -0,0 +1,285 @@
|
||||
---
|
||||
title: HashMap简介
|
||||
tag:
|
||||
- hashmap
|
||||
categories: 数据结构
|
||||
abbrlink: dbb6295a
|
||||
---
|
||||
|
||||
# HashMap简介
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
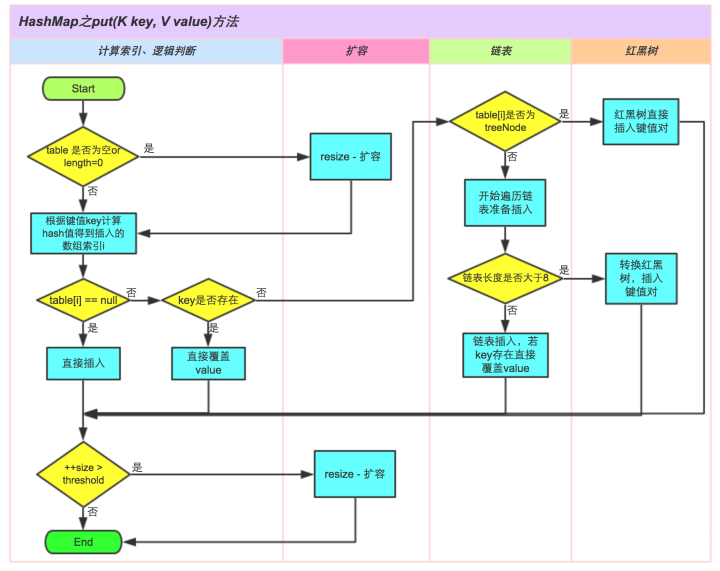
#### HashMap核心数据结构
|
||||
|
||||
|
||||
|
||||
Hash表 = 数组 + 线性链表 + 红黑树
|
||||
|
||||
|
||||
|
||||
#### 为什么初始容量是2的指数幂?
|
||||
|
||||
|
||||
|
||||
如果创建HashMap时指定的大小不是2的指数就会报错吗?
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
Map map = new HashMap<>(13);
|
||||
```
|
||||
|
||||
|
||||
|
||||
这行代码在编译的时候也不会报错,那为什么说初始容量是2的指数呢?
|
||||
|
||||
|
||||
|
||||
看一下HashMap的构造器
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
public HashMap(int initialCapacity, float loadFactor) {
|
||||
if (initialCapacity < 0)
|
||||
throw new IllegalArgumentException("Illegal initial capacity: " +
|
||||
initialCapacity);
|
||||
if (initialCapacity > MAXIMUM_CAPACITY)
|
||||
initialCapacity = MAXIMUM_CAPACITY;
|
||||
if (loadFactor <= 0 || Float.isNaN(loadFactor))
|
||||
throw new IllegalArgumentException("Illegal load factor: " +
|
||||
loadFactor);
|
||||
this.loadFactor = loadFactor;
|
||||
// 调用了tableSizeFor()方法
|
||||
this.threshold = tableSizeFor(initialCapacity);
|
||||
}
|
||||
|
||||
static final int tableSizeFor(int cap) {
|
||||
int n = cap - 1;
|
||||
n |= n >>> 1;
|
||||
n |= n >>> 2;
|
||||
n |= n >>> 4;
|
||||
n |= n >>> 8;
|
||||
n |= n >>> 16;
|
||||
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
tableSizeFor写的奇奇怪怪的嘞, 这一长串是干嘛呢?
|
||||
|
||||
|
||||
|
||||
因为initCapacity必定大于等于0, 所以在他的二进制数中,首位必然是1.而且initCapacity最大值又小于32位.
|
||||
因此,先将他右移一位取或,结果的前两位必然也是1,依次将后续的所有位数全部变成1, 得到的就是他所在的,距离值最近的2^n-1. 最后将该值 +1 就得到了比initCapacity大,且距离最近的2的指数值.
|
||||
|
||||
|
||||
|
||||
那为什么呢? 为什么一定要将容量设置为2的指数呢?初始容量给多少就是多少不行吗?
|
||||
先提一些题外话, 哈希值可以很大也可以很小,如何将这个很大范围的哈希值塞进很小的一个数组里呢?
|
||||
很容易想到的方法就是对这个值取余,这样不管多大的数值,散布在这个数组各个索引的概率也差不多相等.
|
||||
在HashMap中,计算索引的方法是
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
// n = table.length
|
||||
// hash = hash(key)
|
||||
i = (n - 1) & hash
|
||||
|
||||
static final int hash(Object key) {
|
||||
int h;
|
||||
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
因为n都被置为2的指数,n = 0000 0000 0100 0000, n - 1 = 0000 0000 0011 1111,这样做且运算时,hash值前面的位数和0做&计算都是0,直接取hash后几位就可以了,而且这个结果的范围就在0 ~ n-1之间.
|
||||
|
||||
|
||||
|
||||
#### 加载因子为什么是0.75?
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
/*
|
||||
* <p>As a general rule, the default load factor (.75) offers a good
|
||||
* tradeoff between time and space costs. Higher values decrease the
|
||||
* space overhead but increase the lookup cost (reflected in most of
|
||||
* the operations of the <tt>HashMap</tt> class, including
|
||||
* <tt>get</tt> and <tt>put</tt>). The expected number of entries in
|
||||
* the map and its load factor should be taken into account when
|
||||
* setting its initial capacity, so as to minimize the number of
|
||||
* rehash operations. If the initial capacity is greater than the
|
||||
* maximum number of entries divided by the load factor, no rehash
|
||||
* operations will ever occur.
|
||||
*/
|
||||
```
|
||||
|
||||
|
||||
|
||||
从HashMap中摘下来的一段注释, 加载因子决定了当数组填充多少时,才开始扩容.
|
||||
理论上来说数组的每个位置都是有均等的可能放入元素的,那是不是填个1,当所有的位置都占满了才去扩容呢?
|
||||
理论是这样的,但是会有可能发生 有一个位置就是没有数据,其他格子下链的数据已经堆积起来了. 这样去get(key)的时候会花费更长的时间.
|
||||
同样的道理,基于空间上考虑,在尽量数组装的差不多的时候才去考虑扩容.毕竟每个位置放入元素的机会都是均等的.
|
||||
因此,`the default load factor (.75) offers a good tradeoff between time and space costs`.
|
||||
|
||||
|
||||
|
||||
#### 为什么链表长度为8的时候,会去转为红黑树?
|
||||
|
||||
|
||||
|
||||
这里要引入一个泊松分布的概念
|
||||
[泊松分布和指数分布：10分钟教程](http://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html)
|
||||
在HashMap的源码中也有相应的概率显示
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
* 0: 0.60653066
|
||||
* 1: 0.30326533
|
||||
* 2: 0.07581633
|
||||
* 3: 0.01263606
|
||||
* 4: 0.00157952
|
||||
* 5: 0.00015795
|
||||
* 6: 0.00001316
|
||||
* 7: 0.00000094
|
||||
* 8: 0.00000006
|
||||
* more: less than 1 in ten million
|
||||
```
|
||||
|
||||
|
||||
|
||||
可以看到,在链表长度为8的时候概率已经非常小了, 已经小于千万分之一.所以即使在长度超过8的情况下链表会转成红黑树,树的出现依然很少见.
|
||||
`Because TreeNodes are about twice the size of regular nodes.`
|
||||
|
||||
|
||||
|
||||
#### JAVA7的HashMap扩容出现的问题
|
||||
|
||||
|
||||
|
||||
JAVA7中扩容的代码主要是下面这段. 当然,中间还有一段重新计算索引的被我删掉, 考虑的是扩容后链表内存放的数据重新计算数组下标依然一样的情况.
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
for (Entry<K, V> e : table){
|
||||
while (null != e){
|
||||
Entry<K, V> next = e.next;
|
||||
|
||||
e.next = newTable[i];
|
||||
newTable[i] = e;
|
||||
e = next;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
如果进行扩容,扩容后的结果
|
||||
|
||||
|
||||
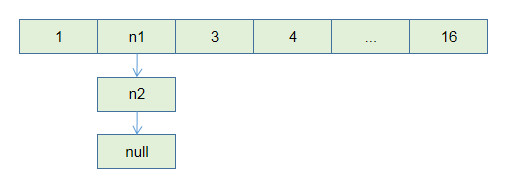
扩容前
|
||||
|
||||
|
||||
|
||||
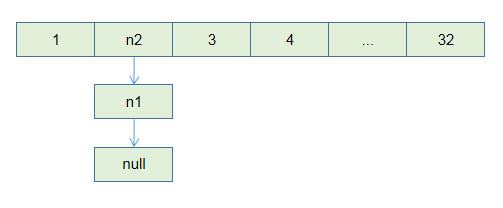
扩容后
|
||||
可以看到,扩容后链表是顺序倒了过来.
|
||||
|
||||
|
||||
|
||||
如果是两个线程同时遇到扩容问题,
|
||||
t1为线程1, e1,next1为t1中的e和next对象.
|
||||
t2为线程2, e2,next2为t2中的e和next对象.
|
||||
若t2在`Entry<K, V> next = e.next;`时挂起,由t1执行,t1执行结束后:
|
||||
|
||||
|
||||
|
||||
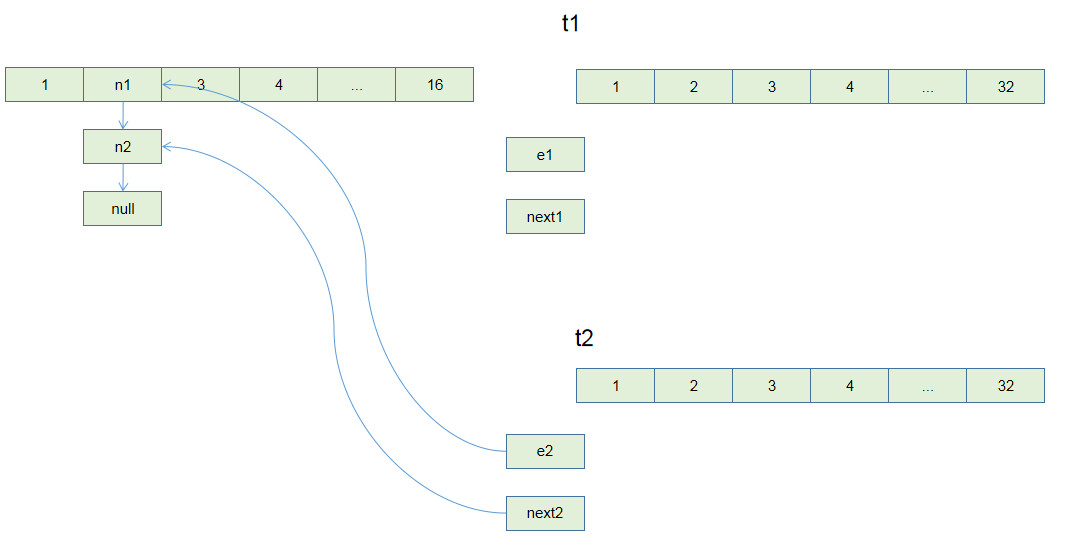
t2挂起
|
||||
根据我们上面看到的扩容后链表顺序返过来,
|
||||
|
||||
|
||||
|
||||
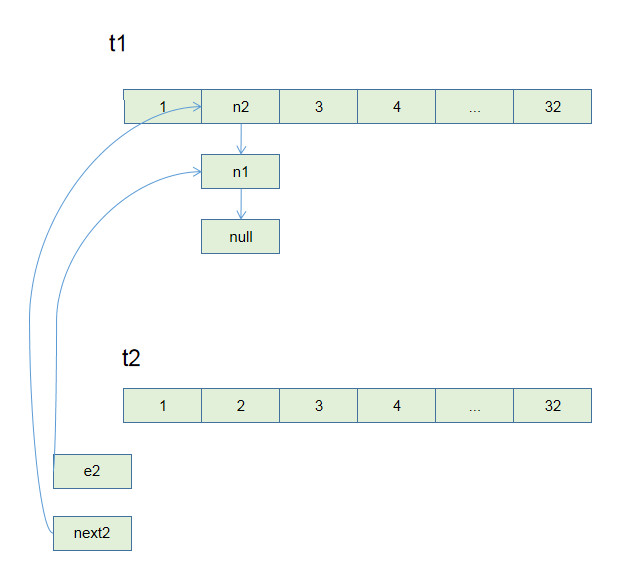
t1执行结束
|
||||
|
||||
|
||||
|
||||
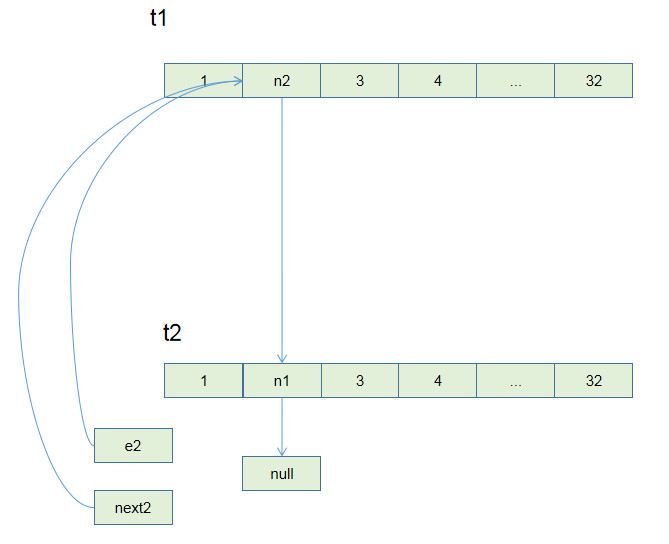
t2第一次循环后
|
||||
|
||||
|
||||
|
||||
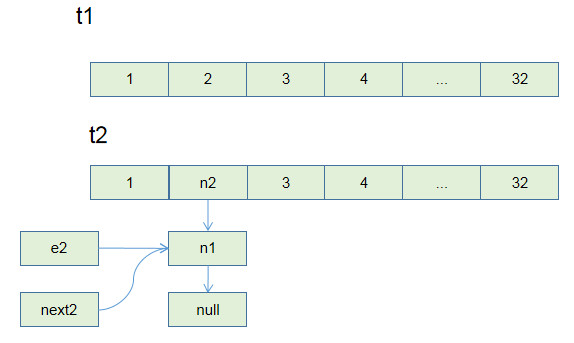
t2第二次循环结束
|
||||
|
||||
第二次循环执行完毕, 在t1时,两次循环后就已经跳出循环. 但是在t2这里, e仍然非空,所以要继续执行.
|
||||
|
||||
|
||||
|
||||
第三次循环执行到`e.next = newTable[i];`时,出现了一个问题
|
||||
|
||||
|
||||
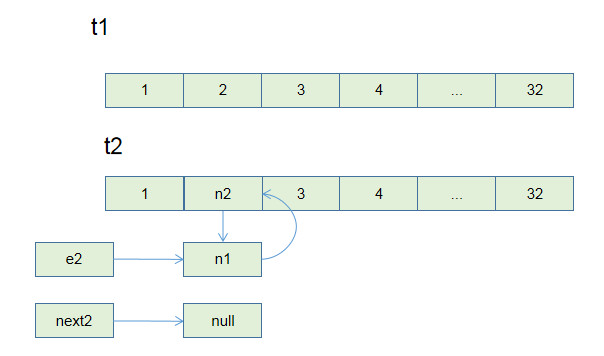
n1.next = n2; n2.next = n1;
|
||||
|
||||
|
||||
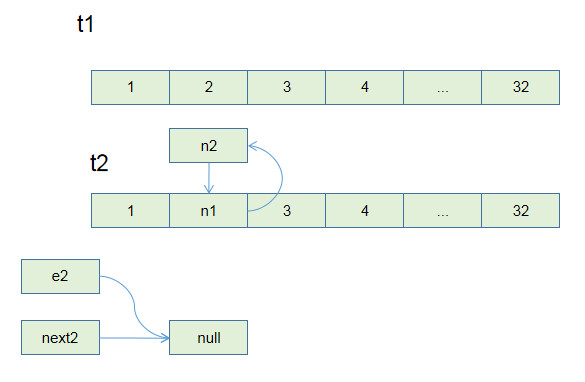
第三次循环结束时
|
||||
第三次循环结束时,e == null 结束循环.
|
||||
但是t2线程中的链表已经形成了一个环状.
|
||||
|
||||
|
||||
|
||||
#### JAVA8的HashMap扩容
|
||||
|
||||
|
||||
|
||||
JAVA8中,HashMap的扩容不再使用重新计算数组下标,挨个移动. 这样就避免了next的指来指去导致链表形成环状的情况.
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
Node<K,V> loHead = null, loTail = null;
|
||||
Node<K,V> hiHead = null, hiTail = null;
|
||||
Node<K,V> next;
|
||||
do {
|
||||
next = e.next;
|
||||
if ((e.hash & oldCap) == 0) {
|
||||
if (loTail == null)
|
||||
loHead = e;
|
||||
else
|
||||
loTail.next = e;
|
||||
loTail = e;
|
||||
}
|
||||
else {
|
||||
if (hiTail == null)
|
||||
hiHead = e;
|
||||
else
|
||||
hiTail.next = e;
|
||||
hiTail = e;
|
||||
}
|
||||
} while ((e = next) != null);
|
||||
if (loTail != null) {
|
||||
loTail.next = null;
|
||||
newTab[j] = loHead;
|
||||
}
|
||||
if (hiTail != null) {
|
||||
hiTail.next = null;
|
||||
newTab[j + oldCap] = hiHead;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
在JAVA8中, 使用的是四个指针,高低位指针,将链表直接分成两段. 低位将低位链表放入新数组的原索引位置, 高位将高位链表放入扩容出的新空间中,相应位置.
|
||||
这样处理避免了挨个元素移动,并且将链表的长度减少.
|
||||
|
||||
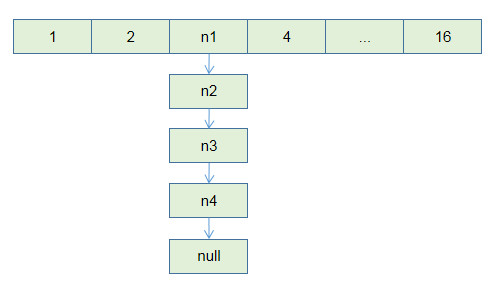
假设有这么一个数组, n1,n3计算结果为低位, n2,n4计算结果为高位.
|
||||
|
||||
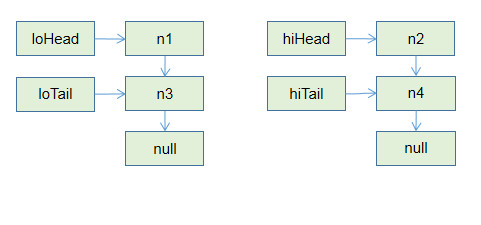
将loHead放到原来的3位置,hiHead放入3+16位置
|
||||
|
||||
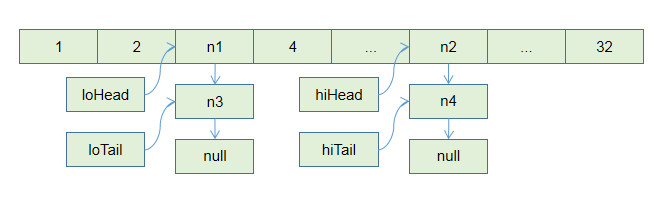
这样就避免了环状的情况,因为hash值和容量做计算的时候,结果始终是一样的.
|
||||
211
source/_posts/data_structure/hashmap/HashMap最大容量.md
Normal file
211
source/_posts/data_structure/hashmap/HashMap最大容量.md
Normal file
@ -0,0 +1,211 @@
|
||||
---
|
||||
title: HashMap的最大容量是多少
|
||||
tag:
|
||||
- hashmap
|
||||
categories: 数据结构
|
||||
abbrlink: 87ddd1f4
|
||||
---
|
||||
|
||||
|
||||
### HashMap的最大容量是多少.
|
||||
|
||||
|
||||
|
||||
首先, HashMap底层是数组+链表, 所以HashMap的容量约等于 `数组长度 * 链表长度`.
|
||||
因为链表长度不固定,甚至可能链表会是树结构, 所以我们主要讨论数组长度.
|
||||
|
||||
|
||||
|
||||
那么, 数组的最大长度是多长呢? 仔细想想, 好像这么多年也没去看过数组的源码(笑).
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
一是规范隐含的限制。Java数组的length必须是非负的int，
|
||||
所以它的理论最大值就是java.lang.Integer.MAX_VALUE = 2^31-1 = 2147483647。
|
||||
|
||||
二是具体的实现带来的限制。
|
||||
这会使得实际的JVM不一定能支持上面说的理论上的最大length。
|
||||
例如说如果有JVM使用uint32_t来记录对象大小的话，那可以允许的最大的数组长度（按元素的个数计算）就会是：
|
||||
(uint32_t的最大值 - 数组对象的对象头大小) / 数组元素大小
|
||||
```
|
||||
|
||||
|
||||
|
||||
嗯..数组长度理论上可以达到 2^31-1 这么长, 那么HashMap的最大长度也是这么了?
|
||||
|
||||
|
||||
|
||||
不, 在HashMap中规定HashMap底层数组的元素最大为 1<<30
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
static final int MAXIMUM_CAPACITY = 1 << 30;
|
||||
```
|
||||
|
||||
|
||||
|
||||
为啥呢? 理论上不是可以更长吗?
|
||||
|
||||
|
||||
|
||||
还记得我们以前提到过的HashMap会把容量定为输入容量的最近的2次幂.
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
static final int tableSizeFor(int cap) {
|
||||
int n = cap - 1;
|
||||
n |= n >>> 1;
|
||||
n |= n >>> 2;
|
||||
n |= n >>> 4;
|
||||
n |= n >>> 8;
|
||||
n |= n >>> 16;
|
||||
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
这串是干嘛呢?
|
||||
|
||||
|
||||
|
||||
现在想象一个场景, `new HashMap(9);`
|
||||
我想初始化一个长度为9的HashMap
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
cap:
|
||||
00000000 00000000 00000000 00001001
|
||||
|
||||
int n = cap - 1:
|
||||
00000000 00000000 00000000 00001000
|
||||
|
||||
n >>> 1:
|
||||
00000000 00000000 00000000 00000100
|
||||
|
||||
n |= n >>> 1:
|
||||
00000000 00000000 00000000 00001100
|
||||
|
||||
n >>> 2:
|
||||
00000000 00000000 00000000 00000011
|
||||
|
||||
n |= n >>> 2:
|
||||
00000000 00000000 00000000 00001111
|
||||
|
||||
n >>> 4:
|
||||
00000000 00000000 00000000 00001111
|
||||
|
||||
n |= n >>> 4:
|
||||
00000000 00000000 00000000 00001111
|
||||
|
||||
|
||||
n >>> 8:
|
||||
00000000 00000000 00000000 00001111
|
||||
|
||||
n |= n >>> 8:
|
||||
00000000 00000000 00000000 00001111
|
||||
|
||||
n >>> 16:
|
||||
00000000 00000000 00000000 00001111
|
||||
|
||||
n |= n >>> 16:
|
||||
00000000 00000000 00000000 00001111
|
||||
```
|
||||
|
||||
|
||||
|
||||
这边计算了什么呢
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
00000000 00000000 00000000 00001111 = 15
|
||||
```
|
||||
|
||||
|
||||
|
||||
也就是将原本最高的一位后面全部变成1
|
||||
也即, 变成了 `2^n -1`
|
||||
这样只要最后结果加1, 就会变成离他最近的2次幂.
|
||||
|
||||
|
||||
|
||||
那这些有什么用呢?
|
||||
|
||||
|
||||
|
||||
`00000000 00000000 00000000 00000001` 左边不是31个位置吗? 为什么最大容量不是 1 << 31 ?
|
||||
|
||||
|
||||
|
||||
如果左移31, 就会变成`10000000 00000000 00000000 00000000`,
|
||||
而最高位, 即最左边的位是符号位, 1为负数.
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
// 运行这条
|
||||
System.out.println(0b10000000_00000000_00000000_00000000);
|
||||
|
||||
// 输出
|
||||
-2147483648
|
||||
```
|
||||
|
||||
|
||||
|
||||
数组长度总不能是负数吧. 所以HashMap的数组长度最长是 1<<30
|
||||
|
||||
------
|
||||
|
||||
尝试了一下添加1<<30个数进HashMap
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
public static void main(String[] args) {
|
||||
int times = 1<<30;
|
||||
Map<Integer, Integer> map = new HashMap<>();
|
||||
for (int i = 0; i < times; i++) {
|
||||
map.put(i, i);
|
||||
System.out.println(i);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
可以看到, 我没有设置HashMap初始大小, 因此默认大小是16, 因为我们知道, HashMap在一定条件下会扩容, 扩容导致的问题就是数据迁移.
|
||||
|
||||
|
||||
|
||||
所以在运行到 1486699 的时候第一次出现明显卡顿,时间很短 大概一秒左右, 再往后的输出停顿时间越来越久.
|
||||
|
||||
|
||||
|
||||
因此小伙伴们如果预先知道要装多少数据, 或者大概数据, 不妨精心计算一下HashMap的初始大小.我认为 总数据量 / (3|4|5|6) 都可以.
|
||||
|
||||
|
||||
|
||||
因为按照同一节点下链表的数据多少规律, 同一个节点下挂载多个数据的概率是逐渐减少的.(而且没有哪个map会装这么多数据吧
|
||||
|
||||
|
||||
|
||||
```plain
|
||||
0: 0.60653066
|
||||
1: 0.30326533
|
||||
2: 0.07581633
|
||||
3: 0.01263606
|
||||
4: 0.00157952
|
||||
5: 0.00015795
|
||||
6: 0.00001316
|
||||
7: 0.00000094
|
||||
8: 0.00000006
|
||||
```
|
||||
|
||||
|
||||
|
||||
在 23739181 的时候就OOM了, 或许下次把堆内存调大点再试试(逃
|
||||
3634
source/_posts/java/base/stream/详细分析JDK中Stream的实现原理.md
Normal file
3634
source/_posts/java/base/stream/详细分析JDK中Stream的实现原理.md
Normal file
File diff suppressed because it is too large
Load Diff
518
source/_posts/java/base/thread/Java线程生命周期与状态切换.md
Normal file
518
source/_posts/java/base/thread/Java线程生命周期与状态切换.md
Normal file
@ -0,0 +1,518 @@
|
||||
---
|
||||
title: Java线程生命周期与状态切换
|
||||
tag:
|
||||
- 多线程
|
||||
- java
|
||||
categories:
|
||||
- 多线程
|
||||
- java
|
||||
abbrlink: 43515
|
||||
date: 2021-08-13 00:00:00
|
||||
---
|
||||
# Java线程生命周期与状态切换
|
||||
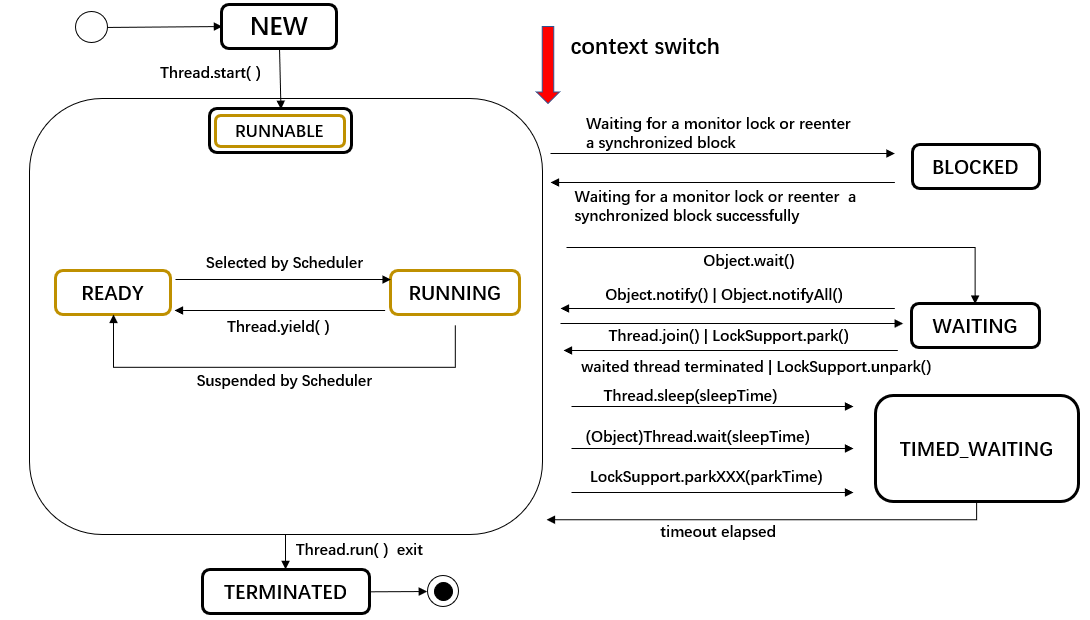[](https://throwable-blog-1256189093.cos.ap-guangzhou.myqcloud.com/202008/j-t-l-s-logo.png)
|
||||
|
||||
## 前提[#](https://www.cnblogs.com/throwable/p/13439079.html#前提)
|
||||
|
||||
最近有点懒散，没什么比较有深度的产出。刚好想重新研读一下`JUC`线程池的源码实现，在此之前先深入了解一下`Java`中的线程实现，包括线程的生命周期、状态切换以及线程的上下文切换等等。编写本文的时候，使用的`JDK`版本是11。
|
||||
|
||||
## Java线程的实现[#](https://www.cnblogs.com/throwable/p/13439079.html#java线程的实现)
|
||||
|
||||
在**JDK1.2之后**，Java线程模型已经确定了基于操作系统原生线程模型实现。因此，目前或者今后的JDK版本中，操作系统支持怎么样的线程模型，在很大程度上决定了Java虚拟机的线程如何映射，这一点在不同的平台上没有办法达成一致，虚拟机规范中也未限定Java线程需要使用哪种线程模型来实现。线程模型只对线程的并发规模和操作成本产生影响，对于Java程序来说，这些差异是透明的。
|
||||
|
||||
对应`Oracle Sun JDK`或者说`Oracle Sun JVM`而言，它的Windows版本和Linux版本都是使用**一对一的线程模型**实现的（如下图所示）。
|
||||
|
||||
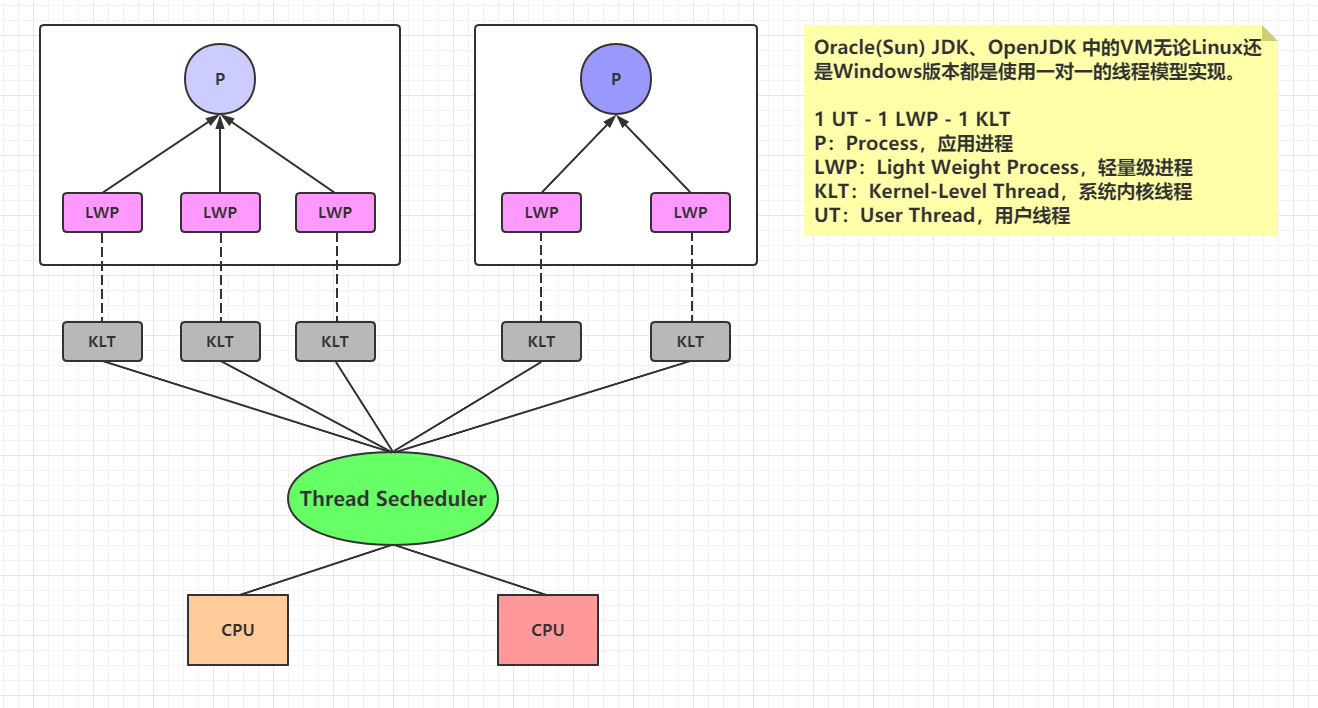[](https://throwable-blog-1256189093.cos.ap-guangzhou.myqcloud.com/202008/j-t-l-s-1.png)
|
||||
|
||||
也就是一条`Java`线程就映射到一条轻量级进程（**Light Weight Process**）中，而一条轻量级线程又映射到一条内核线程（**Kernel-Level Thread**）。我们平时所说的线程，往往就是指轻量级进程（或者通俗来说我们平时新建的`java.lang.Thread`就是轻量级进程实例的一个"句柄"，因为一个`java.lang.Thread`实例会对应`JVM`里面的一个`JavaThread`实例，而`JVM`里面的`JavaThread`就应该理解为轻量级进程）。前面推算这个线程映射关系，可以知道，我们在应用程序中创建或者操作的`java.lang.Thread`实例最终会映射到系统的内核线程，如果我们恶意或者实验性无限创建`java.lang.Thread`实例，最终会影响系统的正常运行甚至导致系统崩溃（可以在`Windows`开发环境中做实验，确保内存足够的情况下使用死循环创建和运行`java.lang.Thread`实例）。
|
||||
|
||||
线程调度方式包括两种，协同式线程调度和抢占式线程调度。
|
||||
|
||||
| 线程调度方式 | 描述 | 劣势 | 优势 |
|
||||
| :------------: | :----------------------------------------------------------: | :-------------------------------------------------: | :------------------------------------: |
|
||||
| 协同式线程调度 | 线程的执行时间由线程本身控制，执行完毕后主动通知操作系统切换到另一个线程上 | 某个线程如果不让出CPU执行时间可能会导致整个系统崩溃 | 实现简单，没有线程同步的问题 |
|
||||
| 抢占式线程调度 | 每个线程由操作系统来分配执行时间，线程的切换不由线程自身决定 | 实现相对复杂，操作系统需要控制线程同步和切换 | 不会出现一个线程阻塞导致系统崩溃的问题 |
|
||||
|
||||
`Java`线程最终会映射为系统内核原生线程，所以`Java`线程调度最终取决于系操作系统，而目前主流的操作系统内核线程调度基本都是使用抢占式线程调度。也就是可以死记硬背一下：**Java线程是使用抢占式线程调度方式进行线程调度的**。
|
||||
|
||||
很多操作系统都提供线程优先级的概念，但是由于平台特性的问题，Java中的线程优先级和不同平台中系统线程优先级并不匹配，所以Java线程优先级可以仅仅理解为“**建议优先级**”，通俗来说就是`java.lang.Thread#setPriority(int newPriority)`并不一定生效，**有可能Java线程的优先级会被系统自行改变**。
|
||||
|
||||
## Java线程的状态切换[#](https://www.cnblogs.com/throwable/p/13439079.html#java线程的状态切换)
|
||||
|
||||
`Java`线程的状态可以从`java.lang.Thread`的内部枚举类`java.lang.Thread$State`得知：
|
||||
|
||||
```java
|
||||
public enum State {
|
||||
|
||||
NEW,
|
||||
|
||||
RUNNABLE,
|
||||
|
||||
BLOCKED,
|
||||
|
||||
WAITING,
|
||||
|
||||
TIMED_WAITING,
|
||||
|
||||
TERMINATED;
|
||||
}
|
||||
```
|
||||
|
||||
这些状态的描述总结成图如下：
|
||||
|
||||
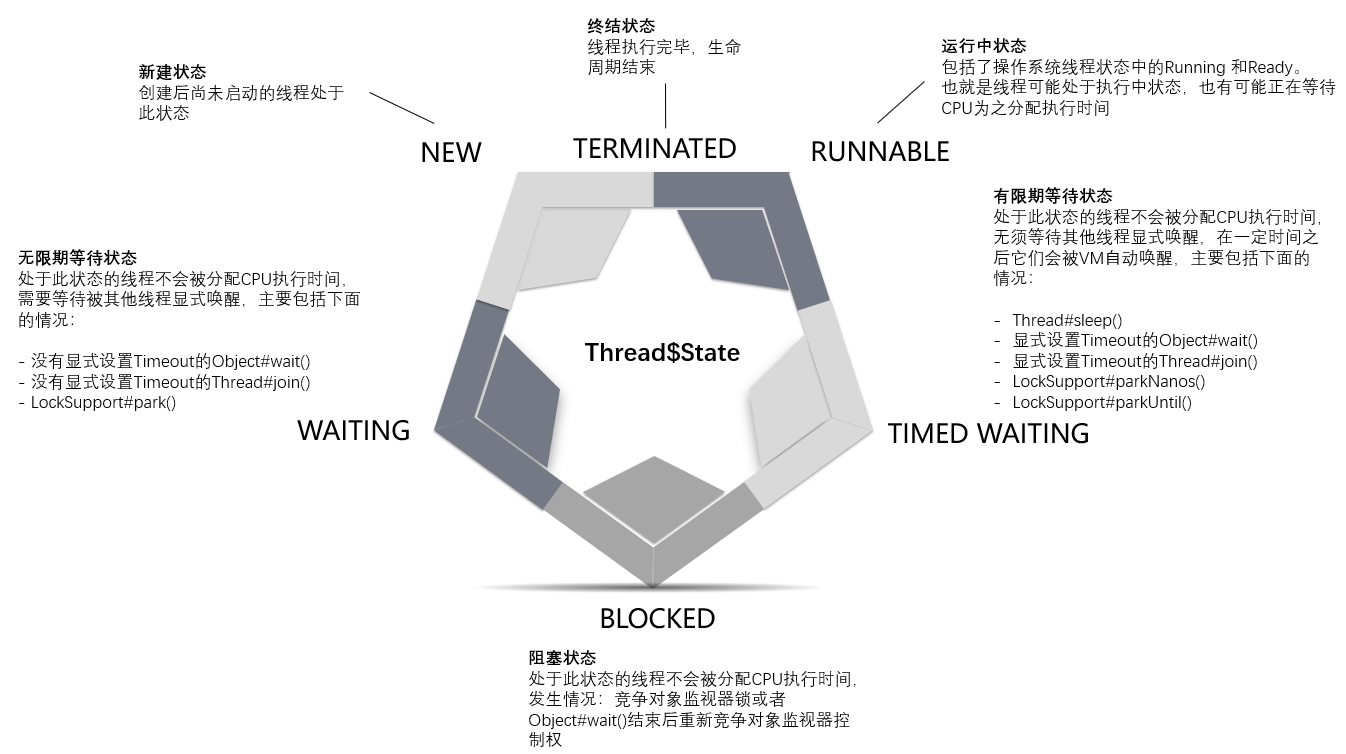[](https://throwable-blog-1256189093.cos.ap-guangzhou.myqcloud.com/202008/j-t-l-s-3.png)
|
||||
|
||||
**线程状态之间关系切换**图如下：
|
||||
|
||||
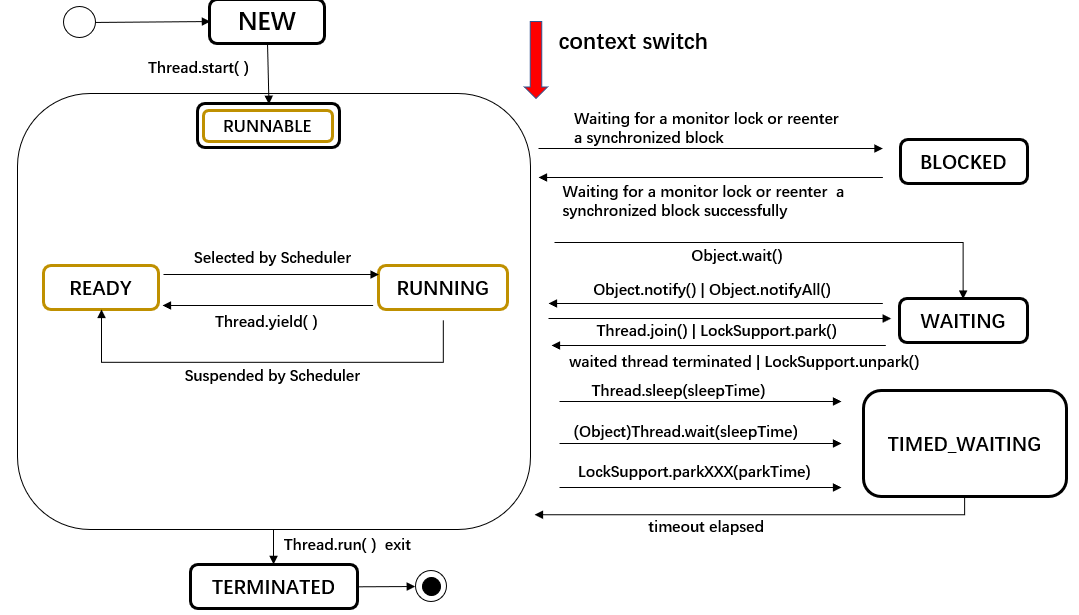[](https://throwable-blog-1256189093.cos.ap-guangzhou.myqcloud.com/202008/j-t-l-s-2.png)
|
||||
|
||||
下面通过API注释和一些简单的代码例子分析一下Java线程的状态含义和状态切换。
|
||||
|
||||
### NEW状态[#](https://www.cnblogs.com/throwable/p/13439079.html#new状态)
|
||||
|
||||
**API注释**：
|
||||
|
||||
```java
|
||||
/**
|
||||
* Thread state for a thread which has not yet started.
|
||||
*
|
||||
*/
|
||||
NEW,
|
||||
```
|
||||
|
||||
> 线程实例尚未启动时候的线程状态。
|
||||
|
||||
一个刚创建而尚未启动（尚未调用`Thread#start()`方法）的Java线程实例的就是处于`NEW`状态。
|
||||
|
||||
```java
|
||||
public class ThreadState {
|
||||
|
||||
public static void main(String[] args) throws Exception {
|
||||
Thread thread = new Thread();
|
||||
System.out.println(thread.getState());
|
||||
}
|
||||
}
|
||||
|
||||
// 输出结果
|
||||
NEW
|
||||
```
|
||||
|
||||
### RUNNABLE状态[#](https://www.cnblogs.com/throwable/p/13439079.html#runnable状态)
|
||||
|
||||
**API注释**：
|
||||
|
||||
```java
|
||||
/**
|
||||
* Thread state for a runnable thread. A thread in the runnable
|
||||
* state is executing in the Java virtual machine but it may
|
||||
* be waiting for other resources from the operating system
|
||||
* such as processor.
|
||||
*/
|
||||
RUNNABLE,
|
||||
```
|
||||
|
||||
> 可运行状态下线程的线程状态。可运行状态下的线程在Java虚拟机中执行，但它可能执行等待操作系统的其他资源，例如处理器。
|
||||
|
||||
当Java线程实例调用了`Thread#start()`之后，就会进入`RUNNABLE`状态。`RUNNABLE`状态可以认为包含两个子状态：`READY`和`RUNNING`。
|
||||
|
||||
- `READY`：该状态的线程可以被线程调度器进行调度使之更变为`RUNNING`状态。
|
||||
- `RUNNING`：该状态表示线程正在运行，线程对象的`run()`方法中的代码所对应的的指令正在被CPU执行。
|
||||
|
||||
当Java线程实例`Thread#yield()`方法被调用时或者由于线程调度器的调度，线程实例的状态有可能由`RUNNING`转变为`READY`，但是从线程状态`Thread#getState()`获取到的状态依然是`RUNNABLE`。例如：
|
||||
|
||||
```java
|
||||
public class ThreadState1 {
|
||||
|
||||
public static void main(String[] args) throws Exception {
|
||||
Thread thread = new Thread(()-> {
|
||||
while (true){
|
||||
Thread.yield();
|
||||
}
|
||||
});
|
||||
thread.start();
|
||||
Thread.sleep(2000);
|
||||
System.out.println(thread.getState());
|
||||
}
|
||||
}
|
||||
// 输出结果
|
||||
RUNNABLE
|
||||
```
|
||||
|
||||
### WAITING状态[#](https://www.cnblogs.com/throwable/p/13439079.html#waiting状态)
|
||||
|
||||
**API注释**：
|
||||
|
||||
```java
|
||||
/**
|
||||
* Thread state for a waiting thread.
|
||||
* A thread is in the waiting state due to calling one of the
|
||||
* following methods:
|
||||
* <ul>
|
||||
* <li>{@link Object#wait() Object.wait} with no timeout</li>
|
||||
* <li>{@link #join() Thread.join} with no timeout</li>
|
||||
* <li>{@link LockSupport#park() LockSupport.park}</li>
|
||||
* </ul>
|
||||
*
|
||||
* <p>A thread in the waiting state is waiting for another thread to
|
||||
* perform a particular action.
|
||||
*
|
||||
* For example, a thread that has called {@code Object.wait()}
|
||||
* on an object is waiting for another thread to call
|
||||
* {@code Object.notify()} or {@code Object.notifyAll()} on
|
||||
* that object. A thread that has called {@code Thread.join()}
|
||||
* is waiting for a specified thread to terminate.
|
||||
*/
|
||||
WAITING,
|
||||
```
|
||||
|
||||
> 等待中线程的状态。一个线程进入等待状态是由于调用了下面方法之一：
|
||||
> 不带超时的Object#wait()
|
||||
> 不带超时的Thread#join()
|
||||
> LockSupport.park()
|
||||
> 一个处于等待状态的线程总是在等待另一个线程进行一些特殊的处理。
|
||||
> 例如：一个线程调用了Object#wait()，那么它在等待另一个线程调用对象上的Object#notify()或者Object#notifyAll()；一个线程调用了Thread#join()，那么它在等待另一个线程终结。
|
||||
|
||||
`WAITING`是**无限期的等待状态**，这种状态下的线程不会被分配CPU执行时间。当一个线程执行了某些方法之后就会进入无限期等待状态，直到被显式唤醒，被唤醒后，线程状态由`WAITING`更变为`RUNNABLE`然后继续执行。
|
||||
|
||||
| `RUNNABLE`转换为`WAITING`的方法（无限期等待） | `WAITING`转换为`RUNNABLE`的方法（唤醒） |
|
||||
| :-------------------------------------------: | :-------------------------------------: |
|
||||
| `Object#wait()` | `Object#notify() | Object#notifyAll()` |
|
||||
| `Thread#join()` | - |
|
||||
| `LockSupport.part()` | `LockSupport.unpart(thread)` |
|
||||
|
||||
其中`Thread#join()`方法相对比较特殊，它会阻塞线程实例直到线程实例执行完毕，可以观察它的源码如下：
|
||||
|
||||
```java
|
||||
public final void join() throws InterruptedException {
|
||||
join(0);
|
||||
}
|
||||
|
||||
public final synchronized void join(long millis)throws InterruptedException {
|
||||
long base = System.currentTimeMillis();
|
||||
long now = 0;
|
||||
|
||||
if (millis < 0) {
|
||||
throw new IllegalArgumentException("timeout value is negative");
|
||||
}
|
||||
|
||||
if (millis == 0) {
|
||||
while (isAlive()) {
|
||||
wait(0);
|
||||
}
|
||||
} else {
|
||||
while (isAlive()) {
|
||||
long delay = millis - now;
|
||||
if (delay <= 0) {
|
||||
break;
|
||||
}
|
||||
wait(delay);
|
||||
now = System.currentTimeMillis() - base;
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
可见`Thread#join()`是在线程实例存活的时候总是调用`Object#wait()`方法，也就是必须在线程执行完毕`isAlive()`为false（意味着线程生命周期已经终结）的时候才会解除阻塞。
|
||||
|
||||
基于`WAITING`状态举个例子：
|
||||
|
||||
```java
|
||||
public class ThreadState3 {
|
||||
|
||||
public static void main(String[] args) throws Exception {
|
||||
Thread thread = new Thread(()-> {
|
||||
LockSupport.park();
|
||||
while (true){
|
||||
Thread.yield();
|
||||
}
|
||||
});
|
||||
thread.start();
|
||||
Thread.sleep(50);
|
||||
System.out.println(thread.getState());
|
||||
LockSupport.unpark(thread);
|
||||
Thread.sleep(50);
|
||||
System.out.println(thread.getState());
|
||||
}
|
||||
}
|
||||
// 输出结果
|
||||
WAITING
|
||||
RUNNABLE
|
||||
```
|
||||
|
||||
### TIMED WAITING状态[#](https://www.cnblogs.com/throwable/p/13439079.html#timed-waiting状态)
|
||||
|
||||
**API注释**：
|
||||
|
||||
```java
|
||||
/**
|
||||
* Thread state for a waiting thread with a specified waiting time.
|
||||
* A thread is in the timed waiting state due to calling one of
|
||||
* the following methods with a specified positive waiting time:
|
||||
* <ul>
|
||||
* <li>{@link #sleep Thread.sleep}</li>
|
||||
* <li>{@link Object#wait(long) Object.wait} with timeout</li>
|
||||
* <li>{@link #join(long) Thread.join} with timeout</li>
|
||||
* <li>{@link LockSupport#parkNanos LockSupport.parkNanos}</li>
|
||||
* <li>{@link LockSupport#parkUntil LockSupport.parkUntil}</li>
|
||||
* </ul>
|
||||
*/
|
||||
TIMED_WAITING,
|
||||
```
|
||||
|
||||
> 定义了具体等待时间的等待中线程的状态。一个线程进入该状态是由于指定了具体的超时期限调用了下面方法之一：
|
||||
> Thread.sleep()
|
||||
> 带超时的Object#wait()
|
||||
> 带超时的Thread#join()
|
||||
> LockSupport.parkNanos()
|
||||
> LockSupport.parkUntil()
|
||||
|
||||
`TIMED WAITING`就是**有限期等待状态**，它和`WAITING`有点相似，这种状态下的线程不会被分配CPU执行时间，不过这种状态下的线程不需要被显式唤醒，只需要等待超时限期到达就会被`VM`唤醒，有点类似于现实生活中的闹钟。
|
||||
|
||||
| `RUNNABLE`转换为`TIMED WAITING`的方法（有限期等待） | `TIMED WAITING`转换为`RUNNABLE`的方法（超时解除等待） |
|
||||
| :-------------------------------------------------: | :---------------------------------------------------: |
|
||||
| `Object#wait(timeout)` | - |
|
||||
| `Thread#sleep(timeout)` | - |
|
||||
| `Thread#join(timeout)` | - |
|
||||
| `LockSupport.parkNanos(timeout)` | - |
|
||||
| `LockSupport.parkUntil(timeout)` | - |
|
||||
|
||||
举个例子：
|
||||
|
||||
```java
|
||||
public class ThreadState4 {
|
||||
|
||||
public static void main(String[] args) throws Exception {
|
||||
Thread thread = new Thread(()-> {
|
||||
try {
|
||||
Thread.sleep(1000);
|
||||
} catch (InterruptedException e) {
|
||||
//ignore
|
||||
}
|
||||
});
|
||||
thread.start();
|
||||
Thread.sleep(50);
|
||||
System.out.println(thread.getState());
|
||||
Thread.sleep(1000);
|
||||
System.out.println(thread.getState());
|
||||
}
|
||||
}
|
||||
// 输出结果
|
||||
TIMED_WAITING
|
||||
TERMINATED
|
||||
```
|
||||
|
||||
### BLOCKED状态[#](https://www.cnblogs.com/throwable/p/13439079.html#blocked状态)
|
||||
|
||||
**API注释**：
|
||||
|
||||
```java
|
||||
/**
|
||||
* Thread state for a thread blocked waiting for a monitor lock.
|
||||
* A thread in the blocked state is waiting for a monitor lock
|
||||
* to enter a synchronized block/method or
|
||||
* reenter a synchronized block/method after calling
|
||||
* {@link Object#wait() Object.wait}.
|
||||
*/
|
||||
BLOCKED,
|
||||
```
|
||||
|
||||
> 此状态表示一个线程正在阻塞等待获取一个监视器锁。如果线程处于阻塞状态，说明线程等待进入同步代码块或者同步方法的监视器锁或者在调用了Object#wait()之后重入同步代码块或者同步方法。
|
||||
|
||||
`BLOCKED`状态也就是阻塞状态，该状态下的线程不会被分配CPU执行时间。线程的状态为`BLOCKED`的时候有两种可能的情况：
|
||||
|
||||
> A thread in the blocked state is waiting for a monitor lock to enter a synchronized block/method
|
||||
|
||||
1. 线程正在等待一个监视器锁，只有获取监视器锁之后才能进入`synchronized`代码块或者`synchronized`方法，在此等待获取锁的过程线程都处于阻塞状态。
|
||||
|
||||
> reenter a synchronized block/method after calling Object#wait()
|
||||
|
||||
1. 线程X步入`synchronized`代码块或者`synchronized`方法后（此时已经释放监视器锁）调用`Object#wait()`方法之后进行阻塞，当接收其他线程T调用该锁对象`Object#notify()/notifyAll()`，但是线程T尚未退出它所在的`synchronized`代码块或者`synchronized`方法，那么线程X依然处于阻塞状态（注意API注释中的**reenter**，理解它场景2就豁然开朗）。
|
||||
|
||||
更加详细的描述可以参考笔者之前写过的一篇文章：[深入理解Object提供的阻塞和唤醒API](http://www.throwable.club/2019/04/30/java-object-wait-notify)
|
||||
|
||||
针对上面的场景1举个简单的例子：
|
||||
|
||||
```java
|
||||
public class ThreadState6 {
|
||||
|
||||
private static final Object MONITOR = new Object();
|
||||
|
||||
public static void main(String[] args) throws Exception {
|
||||
Thread thread1 = new Thread(()-> {
|
||||
synchronized (MONITOR){
|
||||
try {
|
||||
Thread.sleep(Integer.MAX_VALUE);
|
||||
} catch (InterruptedException e) {
|
||||
//ignore
|
||||
}
|
||||
}
|
||||
});
|
||||
Thread thread2 = new Thread(()-> {
|
||||
synchronized (MONITOR){
|
||||
System.out.println("thread2 got monitor lock...");
|
||||
}
|
||||
});
|
||||
thread1.start();
|
||||
Thread.sleep(50);
|
||||
thread2.start();
|
||||
Thread.sleep(50);
|
||||
System.out.println(thread2.getState());
|
||||
}
|
||||
}
|
||||
// 输出结果
|
||||
BLOCKED
|
||||
```
|
||||
|
||||
针对上面的场景2举个简单的例子：
|
||||
|
||||
```java
|
||||
public class ThreadState7 {
|
||||
|
||||
private static final Object MONITOR = new Object();
|
||||
private static final DateTimeFormatter F = DateTimeFormatter.ofPattern("yyyy-MM-dd HH:mm:ss");
|
||||
|
||||
public static void main(String[] args) throws Exception {
|
||||
System.out.println(String.format("[%s]-begin...", F.format(LocalDateTime.now())));
|
||||
Thread thread1 = new Thread(() -> {
|
||||
synchronized (MONITOR) {
|
||||
System.out.println(String.format("[%s]-thread1 got monitor lock...", F.format(LocalDateTime.now())));
|
||||
try {
|
||||
Thread.sleep(1000);
|
||||
MONITOR.wait();
|
||||
} catch (InterruptedException e) {
|
||||
//ignore
|
||||
}
|
||||
System.out.println(String.format("[%s]-thread1 exit waiting...", F.format(LocalDateTime.now())));
|
||||
}
|
||||
});
|
||||
Thread thread2 = new Thread(() -> {
|
||||
synchronized (MONITOR) {
|
||||
System.out.println(String.format("[%s]-thread2 got monitor lock...", F.format(LocalDateTime.now())));
|
||||
try {
|
||||
MONITOR.notify();
|
||||
Thread.sleep(2000);
|
||||
} catch (InterruptedException e) {
|
||||
//ignore
|
||||
}
|
||||
System.out.println(String.format("[%s]-thread2 releases monitor lock...", F.format(LocalDateTime.now())));
|
||||
}
|
||||
});
|
||||
thread1.start();
|
||||
thread2.start();
|
||||
// 这里故意让主线程sleep 1500毫秒从而让thread2调用了Object#notify()并且尚未退出同步代码块，确保thread1调用了Object#wait()
|
||||
Thread.sleep(1500);
|
||||
System.out.println(thread1.getState());
|
||||
System.out.println(String.format("[%s]-end...", F.format(LocalDateTime.now())));
|
||||
}
|
||||
}
|
||||
// 某个时刻的输出如下：
|
||||
[2019-06-20 00:30:22]-begin...
|
||||
[2019-06-20 00:30:22]-thread1 got monitor lock...
|
||||
[2019-06-20 00:30:23]-thread2 got monitor lock...
|
||||
BLOCKED
|
||||
[2019-06-20 00:30:23]-end...
|
||||
[2019-06-20 00:30:25]-thread2 releases monitor lock...
|
||||
[2019-06-20 00:30:25]-thread1 exit waiting...
|
||||
```
|
||||
|
||||
场景2中：
|
||||
|
||||
- 线程2调用`Object#notify()`后睡眠2000毫秒再退出同步代码块，释放监视器锁。
|
||||
- 线程1只睡眠了1000毫秒就调用了`Object#wait()`，此时它已经释放了监视器锁，所以线程2成功进入同步块，线程1处于API注释中所述的`reenter a synchronized block/method`的状态。
|
||||
- 主线程睡眠1500毫秒刚好可以命中线程1处于`reenter`状态并且打印其线程状态，刚好就是`BLOCKED`状态。
|
||||
|
||||
这三点看起来有点绕，多看几次多思考一下应该就能理解。
|
||||
|
||||
### TERMINATED状态[#](https://www.cnblogs.com/throwable/p/13439079.html#terminated状态)
|
||||
|
||||
**API注释**：
|
||||
|
||||
```java
|
||||
/**
|
||||
* Thread state for a terminated thread.
|
||||
* The thread has completed execution.
|
||||
*/
|
||||
TERMINATED;
|
||||
```
|
||||
|
||||
> 终结的线程对应的线程状态，此时线程已经执行完毕。
|
||||
|
||||
`TERMINATED`状态表示线程已经终结。一个线程实例只能被启动一次，准确来说，只会调用一次`Thread#run()`方法，`Thread#run()`方法执行结束之后，线程状态就会更变为`TERMINATED`，意味着线程的生命周期已经结束。
|
||||
|
||||
举个简单的例子：
|
||||
|
||||
```java
|
||||
public class ThreadState8 {
|
||||
|
||||
public static void main(String[] args) throws Exception {
|
||||
Thread thread = new Thread(() -> {
|
||||
|
||||
});
|
||||
thread.start();
|
||||
Thread.sleep(50);
|
||||
System.out.println(thread.getState());
|
||||
}
|
||||
}
|
||||
// 输出结果
|
||||
TERMINATED
|
||||
```
|
||||
|
||||
## 上下文切换[#](https://www.cnblogs.com/throwable/p/13439079.html#上下文切换)
|
||||
|
||||
多线程环境中，当一个线程的状态由`RUNNABLE`转换为非`RUNNABLE`（`BLOCKED`、`WAITING`或者`TIMED_WAITING`）时，相应线程的上下文信息（也就是常说的`Context`，包括`CPU`的寄存器和程序计数器在某一时间点的内容等等）需要被保存，以便线程稍后恢复为`RUNNABLE`状态时能够在之前的执行进度的基础上继续执行。而一个线程的状态由非`RUNNABLE`状态进入`RUNNABLE`状态时可能涉及恢复之前保存的线程上下文信息并且在此基础上继续执行。这里的对**线程的上下文信息进行保存和恢复的过程**就称为上下文切换（`Context Switch`）。
|
||||
|
||||
线程的上下文切换会带来额外的性能开销，这包括保存和恢复线程上下文信息的开销、对线程进行调度的`CPU`时间开销以及`CPU`缓存内容失效的开销（线程所执行的代码从`CPU`缓存中访问其所需要的变量值要比从主内存（`RAM`）中访问响应的变量值要快得多，但是**线程上下文切换会导致相关线程所访问的CPU缓存内容失效，一般是CPU的`L1 Cache`和`L2 Cache`**，使得相关线程稍后被重新调度到运行时其不得不再次访问主内存中的变量以重新创建`CPU`缓存内容）。
|
||||
|
||||
在`Linux`系统中，可以通过`vmstat`命令来查看全局的上下文切换的次数，例如：
|
||||
|
||||
```shell
|
||||
$ vmstat 1
|
||||
```
|
||||
|
||||
对于`Java`程序的运行，在`Linux`系统中也可以通过`perf`命令进行监视，例如：
|
||||
|
||||
```shell
|
||||
$ perf stat -e cpu-clock,task-clock,cs,cache-reference,cache-misses java YourJavaClass
|
||||
```
|
||||
|
||||
参考资料中提到`Windows`系统下可以通过自带的工具`perfmon`（其实也就是任务管理器）来监视线程的上下文切换，实际上笔者并没有从任务管理器发现有任何办法查看上下文切换，通过搜索之后发现了一个工具：[Process Explorer](https://docs.microsoft.com/zh-cn/sysinternals/downloads/process-explorer)。运行`Process Explorer`同时运行一个`Java`程序并且查看其状态：
|
||||
|
||||
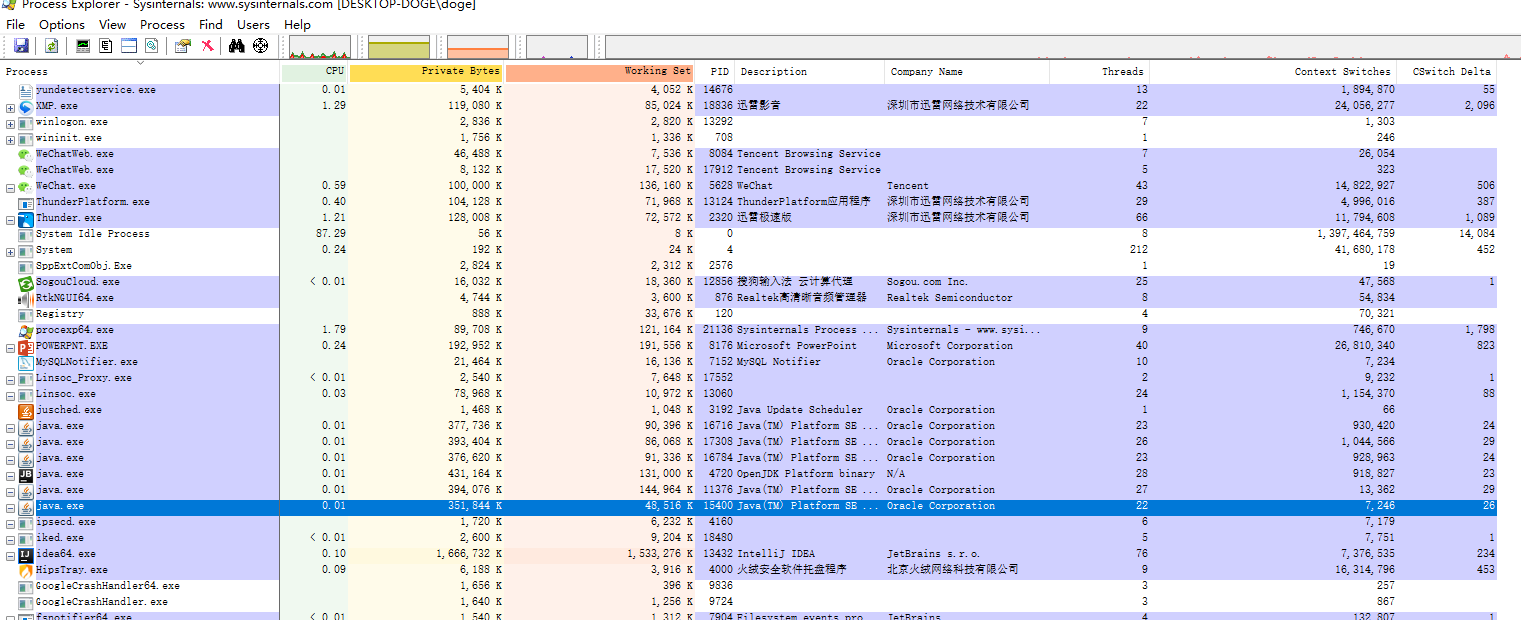[](https://throwable-blog-1256189093.cos.ap-guangzhou.myqcloud.com/202008/j-t-l-s-4.png)
|
||||
|
||||
因为打了断点，可以看到运行中的程序的上下文切换一共7000多次，当前一秒的上下文切换增量为26（因为笔者设置了`Process Explorer`每秒刷新一次数据）。
|
||||
|
||||
## 监控线程状态[#](https://www.cnblogs.com/throwable/p/13439079.html#监控线程状态)
|
||||
|
||||
如果项目在生产环境中运行，不可能频繁调用`Thread#getState()`方法去监测线程的状态变化。JDK本身提供了一些监控线程状态的工具，还有一些开源的轻量级工具如阿里的[Arthas](https://alibaba.github.io/arthas/)，这里简单介绍一下。
|
||||
|
||||
### 使用jvisualvm[#](https://www.cnblogs.com/throwable/p/13439079.html#使用jvisualvm)
|
||||
|
||||
`jvisualvm`是JDK自带的堆、线程等待JVM指标监控工具，适合使用于开发和测试环境。它位于`JAVA_HOME/bin`目录之下。
|
||||
|
||||
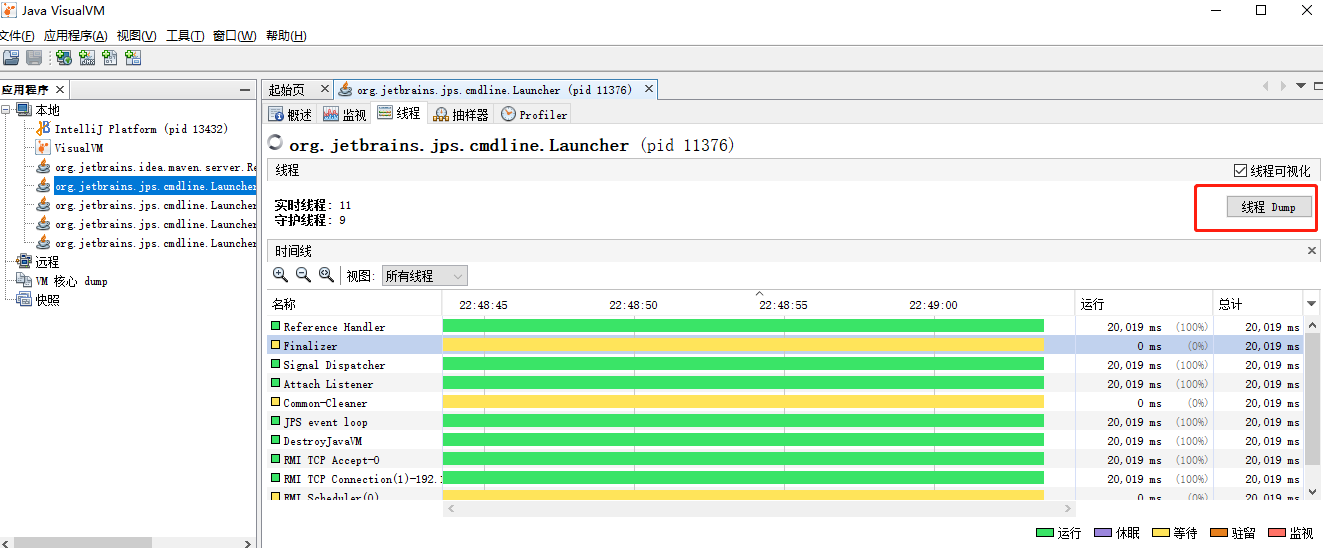[](https://throwable-blog-1256189093.cos.ap-guangzhou.myqcloud.com/202008/j-t-l-s-5.png)
|
||||
|
||||
其中`线程Dump`的按钮类似于下面要提到的`jstack`命令，用于导出所有线程的栈信息。
|
||||
|
||||
### 使用jstack[#](https://www.cnblogs.com/throwable/p/13439079.html#使用jstack)
|
||||
|
||||
`jstack`是JDK自带的命令行工具，功能是用于获取指定PID的Java进程的线程栈信息。例如本地运行的一个`IDEA`实例的`PID`是11376，那么只需要输入：
|
||||
|
||||
```shell
|
||||
jstack 11376
|
||||
```
|
||||
|
||||
然后控制台输出如下：
|
||||
|
||||
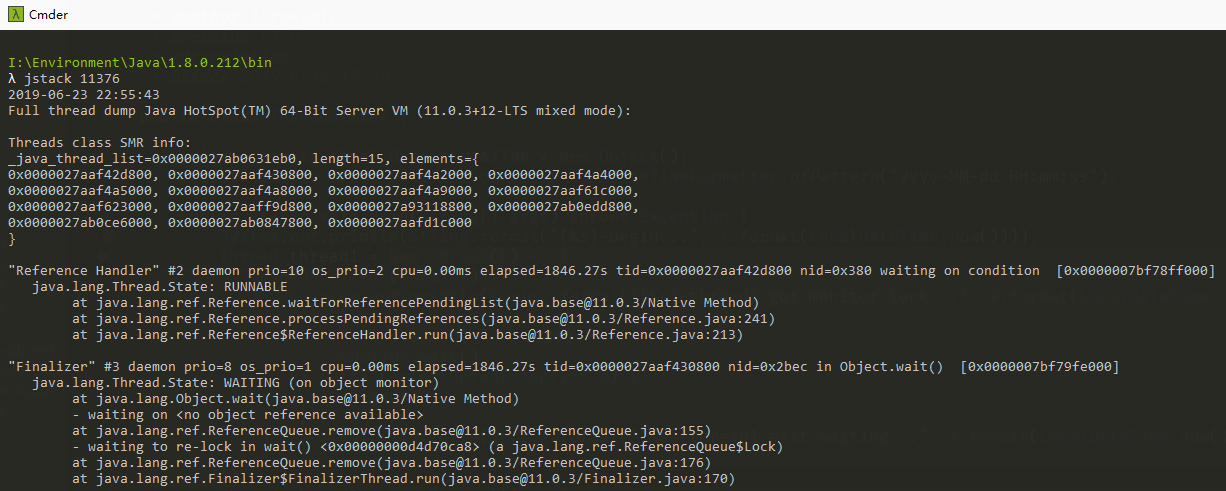[](https://throwable-blog-1256189093.cos.ap-guangzhou.myqcloud.com/202008/j-t-l-s-6.png)
|
||||
|
||||
另外，如果想要定位具体Java进程的`PID`，可以使用`jps`命令。
|
||||
|
||||
### 使用JMC[#](https://www.cnblogs.com/throwable/p/13439079.html#使用jmc)
|
||||
|
||||
`JMC`也就是`Java Mission Control`，它也是JDK自带的工具，提供的功能要比`jvisualvm`强大，包括MBean的处理、线程栈已经状态查看、飞行记录器等等。
|
||||
|
||||
[](https://throwable-blog-1256189093.cos.ap-guangzhou.myqcloud.com/202008/j-t-l-s-7.png)
|
||||
|
||||
## 小结[#](https://www.cnblogs.com/throwable/p/13439079.html#小结)
|
||||
|
||||
理解Java线程状态的切换和一些监控手段，更有利于日常开发多线程程序，对于生产环境出现问题，通过监控线程的栈信息能够快速定位到问题的根本原因（通常来说，目前比较主流的`MVC`应用（准确来说应该是`Servlet`容器如`Tomcat`）都是通过一个线程处理一个单独的请求，当请求出现阻塞的时候，导出对应处理请求的线程基本可以定位到阻塞的精准位置，如果使用消息队列例如`RabbitMQ`，消费者线程出现阻塞也可以利用相似的思路解决）。
|
||||
587
source/_posts/java/base/thread/synchronized实现原理.md
Normal file
587
source/_posts/java/base/thread/synchronized实现原理.md
Normal file
@ -0,0 +1,587 @@
|
||||
---
|
||||
title: synchronized 实现原理
|
||||
tag:
|
||||
- 多线程
|
||||
- java
|
||||
categories:
|
||||
- 多线程
|
||||
- java
|
||||
abbrlink: f11fd659
|
||||
---
|
||||
|
||||
## synchronized 实现原理
|
||||
|
||||
2020-03-24
|
||||
|
||||
# synchronized 实现原理
|
||||
|
||||
## 前言
|
||||
|
||||
众所周知 `synchronized` 锁在 `Java` 中经常使用它的源码是 `C++` 实现的，它的实现原理是怎样的呢？本文以 `OpenJDK 8` 为例探究以下内容。
|
||||
|
||||
- synchronized 是如何工作的
|
||||
- synchronized 锁升级过程
|
||||
- 重量级锁的队列之间协作过程和策略
|
||||
|
||||
## 对象头
|
||||
|
||||
对象头的内容非常多这里我们只做简单介绍以引出后文。在 JVM 中对象布局分为三块区域：
|
||||
|
||||
- 对象头
|
||||
- 实例数据
|
||||
- 对齐填充
|
||||
|
||||
|
||||
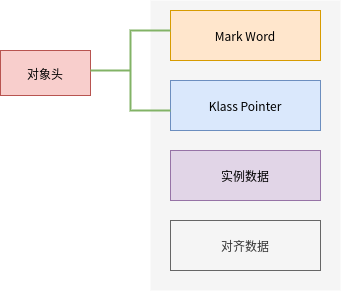
当线程访问同步块时首先需要获得锁并把相关信息存储在对象头中。所以 `wait`、`notify`、`notifyAll` 这些方法为什么被设计在 `Object` 中或许你已经找到答案了。
|
||||
|
||||
Hotspot 有两种对象头：
|
||||
|
||||
- 数组类型，使用 `arrayOopDesc` 来描述对象头
|
||||
- 其它，使用 `instanceOopDesc` 来描述对象头
|
||||
|
||||
对象头由两部分组成
|
||||
|
||||
- Mark Word：存储自身的运行时数据，例如 HashCode、GC 年龄、锁相关信息等内容。
|
||||
- Klass Pointer：类型指针指向它的类元数据的指针。
|
||||
|
||||
64 位虚拟机 Mark Word 是 64bit 其结构如下：
|
||||
|
||||
|
||||
|
||||
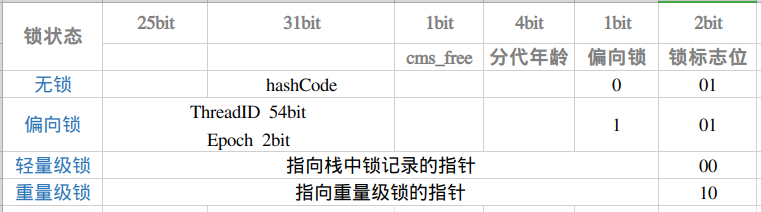
在 JDK 6 中虚拟机团队对锁进行了重要改进，优化了其性能引入了 `偏向锁`、`轻量级锁`、`适应性自旋`、`锁消除`、`锁粗化`等实现，其中 `锁消除`和`锁粗化`本文不做详细讨论其余内容我们将对其进行逐一探究。
|
||||
|
||||
总体上来说锁状态升级流程如下：
|
||||
|
||||
|
||||
|
||||
## 偏向锁
|
||||
|
||||
### 流程
|
||||
|
||||
当线程访问同步块并获取锁时处理流程如下：
|
||||
|
||||
1. 检查 `mark word` 的`线程 id` 。
|
||||
2. 如果为空则设置 CAS 替换当前线程 id。如果替换成功则获取锁成功，如果失败则撤销偏向锁。
|
||||
3. 如果不为空则检查 `线程 id`为是否为本线程。如果是则获取锁成功，如果失败则撤销偏向锁。
|
||||
|
||||
持有偏向锁的线程以后每次进入这个锁相关的同步块时，只需比对一下 mark word 的线程 id 是否为本线程，如果是则获取锁成功。
|
||||
|
||||
如果发生线程竞争发生 2、3 步失败的情况则需要撤销偏向锁。
|
||||
|
||||
### 偏向锁的撤销
|
||||
|
||||
1. 偏向锁的撤销动作必须等待全局安全点
|
||||
2. 暂停拥有偏向锁的线程，判断锁对象是否处于被锁定状态
|
||||
3. 撤销偏向锁恢复到无锁（标志位为 01）或轻量级锁（标志位为 00）的状态
|
||||
|
||||
### 优点
|
||||
|
||||
只有一个线程执行同步块时进一步提高性能，适用于一个线程反复获得同一锁的情况。偏向锁可以提高带有同步但无竞争的程序性能。
|
||||
|
||||
### 缺点
|
||||
|
||||
如果存在竞争会带来额外的锁撤销操作。
|
||||
|
||||
## 轻量级锁
|
||||
|
||||
### 加锁
|
||||
|
||||
多个线程竞争偏向锁导致偏向锁升级为轻量级锁
|
||||
|
||||
1. JVM 在当前线程的栈帧中创建 Lock Reocrd，并将对象头中的 Mark Word 复制到 Lock Reocrd 中。（Displaced Mark Word）
|
||||
2. 线程尝试使用 CAS 将对象头中的 Mark Word 替换为指向 Lock Reocrd 的指针。如果成功则获得锁，如果失败则先检查对象的 Mark Word 是否指向当前线程的栈帧如果是则说明已经获取锁，否则说明其它线程竞争锁则膨胀为重量级锁。
|
||||
|
||||
### 解锁
|
||||
|
||||
1. 使用 CAS 操作将 Mark Word 还原
|
||||
2. 如果第 1 步执行成功则释放完成
|
||||
3. 如果第 1 步执行失败则膨胀为重量级锁。
|
||||
|
||||
### 优点
|
||||
|
||||
其性能提升的依据是对于绝大部分的锁在整个生命周期内都是不会存在竞争。在多线程交替执行同步块的情况下，可以避免重量级锁引起的性能消耗。
|
||||
|
||||
### 缺点
|
||||
|
||||
在有多线程竞争的情况下轻量级锁增加了额外开销。
|
||||
|
||||
## 自旋锁
|
||||
|
||||
自旋是一种获取锁的机制并不是一个锁状态。在膨胀为重量级锁的过程中或重入时会多次尝试自旋获取锁以避免线程唤醒的开销，但是它会占用 CPU 的时间因此如果同步代码块执行时间很短自旋等待的效果就很好，反之则浪费了 CPU 资源。默认情况下自旋次数是 10 次用户可以使用参数 `-XX : PreBlockSpin` 来更改。那么如何优化来避免此情况发生呢？我们来看适应性自旋。
|
||||
|
||||
### 适应性自旋锁
|
||||
|
||||
JDK 6 引入了自适应自旋锁，意味着自旋的次数不在固定，而是由前一次在同一个锁上的自旋时间及锁的拥有者的状态来决定。如果对于某个锁很少自旋成功那么以后有可能省略掉自旋过程以避免资源浪费。有了自适应自旋随着程序运行和性能监控信息的不断完善，虚拟机对程序锁的状况预测就会越来越准确，虛拟机就会变得越来越“聪明”了。
|
||||
|
||||
### 优点
|
||||
|
||||
竞争的线程不会阻塞挂起，提高了程序响应速度。避免重量级锁引起的性能消耗。
|
||||
|
||||
### 缺点
|
||||
|
||||
如果线程始终无法获取锁，自旋消耗 CPU 最终会膨胀为重量级锁。
|
||||
|
||||
## 重量级锁
|
||||
|
||||
在重量级锁中没有竞争到锁的对象会 park 被挂起，退出同步块时 unpark 唤醒后续线程。唤醒操作涉及到操作系统调度会有额外的开销。
|
||||
|
||||
`ObjectMonitor` 中包含一个同步队列（由 `_cxq` 和 `_EntryList` 组成）一个等待队列（ `_WaitSet` ）。
|
||||
|
||||
- 被`notify`或 `notifyAll` 唤醒时根据 `policy` 策略选择加入的队列（policy 默认为 0）
|
||||
- 退出同步块时根据 `QMode` 策略来唤醒下一个线程（QMode 默认为 0）
|
||||
|
||||
这里稍微提及一下**管程**这个概念。synchronized 关键字及 `wait`、`notify`、`notifyAll` 这三个方法都是管程的组成部分。可以说管程就是一把解决并发问题的万能钥匙。有两大核心问题管程都是能够解决的：
|
||||
|
||||
- **互斥**：即同一时刻只允许一个线程访问共享资源；
|
||||
- **同步**：即线程之间如何通信、协作。
|
||||
|
||||
`synchronized` 的 `monitor`锁机制和 JDK 并发包中的 `AQS` 是很相似的，只不过 `AQS` 中是一个同步队列多个等待队列。熟悉 `AQS` 的同学可以拿来做个对比。
|
||||
|
||||
### 队列协作流程图
|
||||
|
||||
|
||||
|
||||
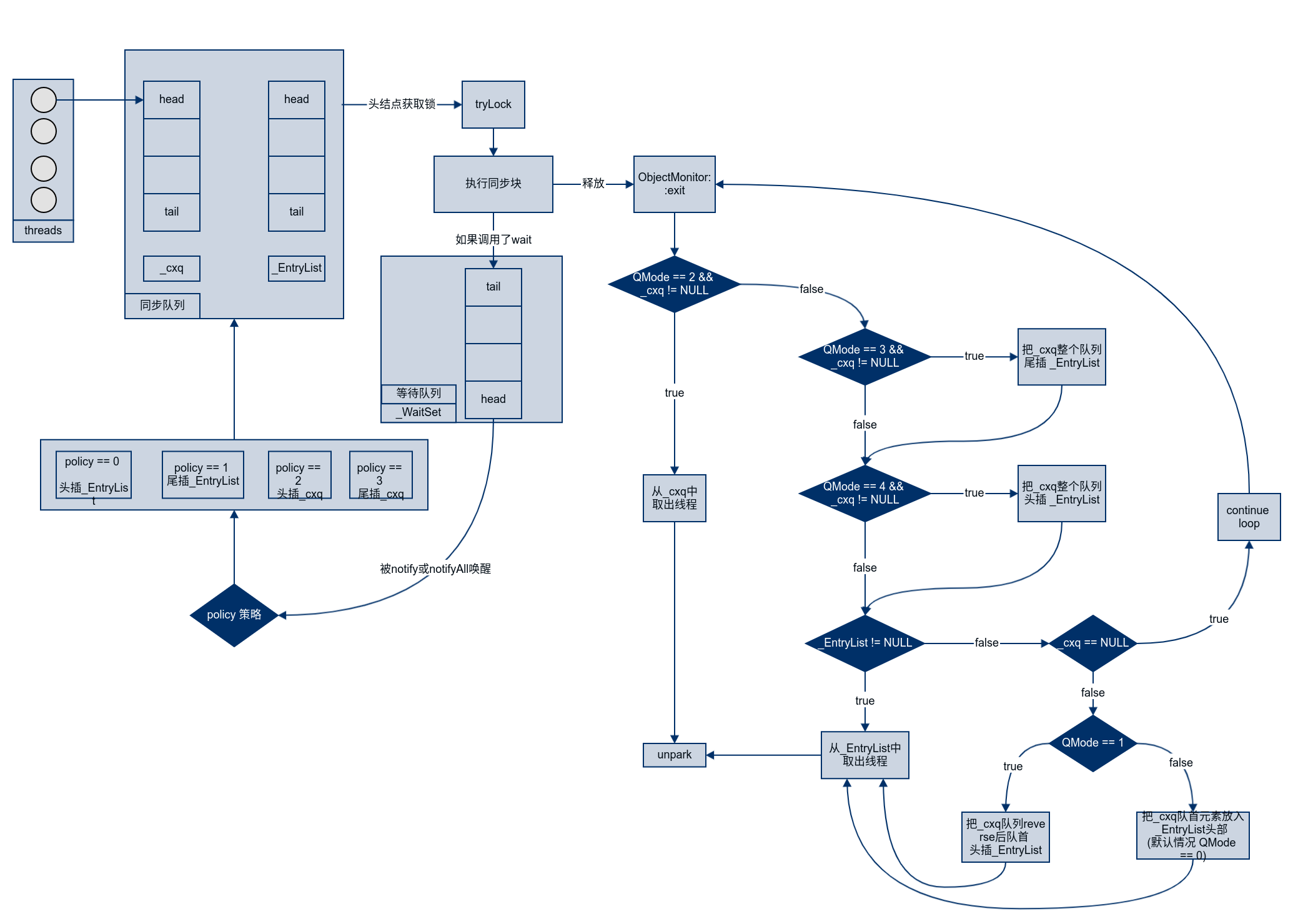
## 源码分析
|
||||
|
||||
在 HotSpot 中 monitor 是由 ObjectMonitor 实现的。其源码是用 c++来实现的源文件是 ObjectMonitor.hpp 主要数据结构如下所示：
|
||||
|
||||
```java
|
||||
ObjectMonitor() {
|
||||
_header = NULL;
|
||||
_count = 0;
|
||||
_waiters = 0, // 等待中的线程数
|
||||
_recursions = 0; // 线程重入次数
|
||||
_object = NULL; // 存储该 monitor 的对象
|
||||
_owner = NULL; // 指向拥有该 monitor 的线程
|
||||
_WaitSet = NULL; // 等待线程 双向循环链表_WaitSet 指向第一个节点
|
||||
_WaitSetLock = 0 ;
|
||||
_Responsible = NULL ;
|
||||
_succ = NULL ;
|
||||
_cxq = NULL ; // 多线程竞争锁时的单向链表
|
||||
FreeNext = NULL ;
|
||||
_EntryList = NULL ; // _owner 从该双向循环链表中唤醒线程，
|
||||
_SpinFreq = 0 ;
|
||||
_SpinClock = 0 ;
|
||||
OwnerIsThread = 0 ;
|
||||
_previous_owner_tid = 0; // 前一个拥有此监视器的线程 ID
|
||||
}
|
||||
```
|
||||
|
||||
> 1. _owner：初始时为 NULL。当有线程占有该 monitor 时 owner 标记为该线程的 ID。当线程释放 monitor 时 owner 恢复为 NULL。owner 是一个临界资源 JVM 是通过 CAS 操作来保证其线程安全的。
|
||||
> 2. _cxq：竞争队列所有请求锁的线程首先会被放在这个队列中（单向）。_cxq 是一个临界资源 JVM 通过 CAS 原子指令来修改_cxq 队列。
|
||||
> 每当有新来的节点入队，它的 next 指针总是指向之前队列的头节点，而_cxq 指针会指向该新入队的节点，所以是后来居上。
|
||||
> 3. _EntryList： _cxq 队列中有资格成为候选资源的线程会被移动到该队列中。
|
||||
> 4. _WaitSet: 等待队列因为调用 wait 方法而被阻塞的线程会被放在该队列中。
|
||||
|
||||
### monitor 竞争过程
|
||||
|
||||
> 1. 通过 CAS 尝试把 monitor 的 owner 字段设置为当前线程。
|
||||
> 2. 如果设置之前的 owner 指向当前线程，说明当前线程再次进入 monitor，即重入锁执行 recursions ++ , 记录重入的次数。
|
||||
> 3. 如果当前线程是第一次进入该 monitor, 设置 recursions 为 1,_owner 为当前线程，该线程成功获得锁并返回。
|
||||
> 4. 如果获取锁失败，则等待锁的释放。
|
||||
|
||||
执行 `monitorenter` 指令时 调用以下代码
|
||||
|
||||
```java
|
||||
IRT_ENTRY_NO_ASYNC(void, InterpreterRuntime::monitorenter(JavaThread* thread, BasicObjectLock* elem))
|
||||
#ifdef ASSERT
|
||||
thread->last_frame().interpreter_frame_verify_monitor(elem);
|
||||
#endif
|
||||
if (PrintBiasedLockingStatistics) {
|
||||
Atomic::inc(BiasedLocking::slow_path_entry_count_addr());
|
||||
}
|
||||
Handle h_obj(thread, elem->obj());
|
||||
assert(Universe::heap()->is_in_reserved_or_null(h_obj()),"must be NULL or an object");
|
||||
// 是否使用偏向锁 JVM 启动时设置的偏向锁-XX:-UseBiasedLocking=false/true
|
||||
if (UseBiasedLocking) {
|
||||
// Retry fast entry if bias is revoked to avoid unnecessary inflation
|
||||
ObjectSynchronizer::fast_enter(h_obj, elem->lock(), true, CHECK);
|
||||
} else {
|
||||
// 轻量级锁
|
||||
ObjectSynchronizer::slow_enter(h_obj, elem->lock(), CHECK);
|
||||
}
|
||||
assert(Universe::heap()->is_in_reserved_or_null(elem->obj()),
|
||||
"must be NULL or an object");
|
||||
#ifdef ASSERT
|
||||
thread->last_frame().interpreter_frame_verify_monitor(elem);
|
||||
#endif
|
||||
IRT_END
|
||||
```
|
||||
|
||||
> `slow_enter` 方法主要是轻量级锁的一些操作，如果操作失败则会膨胀为重量级锁，过程前面已经描述比较清楚此处不在赘述。`enter` 方法则为重量级锁的入口源码如下
|
||||
|
||||
```java
|
||||
void ATTR ObjectMonitor::enter(TRAPS) {
|
||||
Thread * const Self = THREAD ;
|
||||
void * cur ;
|
||||
// 省略部分代码
|
||||
|
||||
// 通过 CAS 操作尝试把 monitor 的_owner 字段设置为当前线程
|
||||
cur = Atomic::cmpxchg_ptr (Self, &_owner, NULL) ;
|
||||
if (cur == NULL) {
|
||||
assert (_recursions == 0 , "invariant") ;
|
||||
assert (_owner == Self, "invariant") ;
|
||||
return ;
|
||||
}
|
||||
|
||||
// 线程重入，recursions++
|
||||
if (cur == Self) {
|
||||
_recursions ++ ;
|
||||
return ;
|
||||
}
|
||||
|
||||
// 如果当前线程是第一次进入该 monitor, 设置_recursions 为 1,_owner 为当前线程
|
||||
if (Self->is_lock_owned ((address)cur)) {
|
||||
assert (_recursions == 0, "internal state error");
|
||||
_recursions = 1 ;
|
||||
_owner = Self ;
|
||||
OwnerIsThread = 1 ;
|
||||
return ;
|
||||
}
|
||||
|
||||
for (;;) {
|
||||
jt->set_suspend_equivalent();
|
||||
// 如果获取锁失败，则等待锁的释放；
|
||||
EnterI (THREAD) ;
|
||||
|
||||
if (!ExitSuspendEquivalent(jt)) break ;
|
||||
_recursions = 0 ;
|
||||
_succ = NULL ;
|
||||
exit (false, Self) ;
|
||||
|
||||
jt->java_suspend_self();
|
||||
}
|
||||
Self->set_current_pending_monitor(NULL);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### monitor 等待
|
||||
|
||||
> 1. 当前线程被封装成 ObjectWaiter 对象 node，状态设置成 ObjectWaiter::TS_CXQ。
|
||||
> 2. for 循环通过 CAS 把 node 节点 push 到`_cxq`列表中，同一时刻可能有多个线程把自己的 node 节点 push 到`_cxq`列表中。
|
||||
> 3. node 节点 push 到_cxq 列表之后，通过自旋尝试获取锁，如果还是没有获取到锁则通过 park 将当前线程挂起等待被唤醒。
|
||||
> 4. 当该线程被唤醒时会从挂起的点继续执行，通过 ObjectMonitor::TryLock 尝试获取锁。
|
||||
|
||||
```java
|
||||
// 省略部分代码
|
||||
void ATTR ObjectMonitor::EnterI (TRAPS) {
|
||||
Thread * Self = THREAD ;
|
||||
assert (Self->is_Java_thread(), "invariant") ;
|
||||
assert (((JavaThread *) Self)->thread_state() == _thread_blocked , "invariant") ;
|
||||
|
||||
// Try lock 尝试获取锁
|
||||
if (TryLock (Self) > 0) {
|
||||
assert (_succ != Self , "invariant") ;
|
||||
assert (_owner == Self , "invariant") ;
|
||||
assert (_Responsible != Self , "invariant") ;
|
||||
// 如果获取成功则退出，避免 park unpark 系统调度的开销
|
||||
return ;
|
||||
}
|
||||
|
||||
// 自旋获取锁
|
||||
if (TrySpin(Self) > 0) {
|
||||
assert (_owner == Self, "invariant");
|
||||
assert (_succ != Self, "invariant");
|
||||
assert (_Responsible != Self, "invariant");
|
||||
return;
|
||||
}
|
||||
|
||||
// 当前线程被封装成 ObjectWaiter 对象 node, 状态设置成 ObjectWaiter::TS_CXQ
|
||||
ObjectWaiter node(Self) ;
|
||||
Self->_ParkEvent->reset() ;
|
||||
node._prev = (ObjectWaiter *) 0xBAD ;
|
||||
node.TState = ObjectWaiter::TS_CXQ ;
|
||||
|
||||
// 通过 CAS 把 node 节点 push 到_cxq 列表中
|
||||
ObjectWaiter * nxt ;
|
||||
for (;;) {
|
||||
node._next = nxt = _cxq ;
|
||||
if (Atomic::cmpxchg_ptr (&node, &_cxq, nxt) == nxt) break ;
|
||||
|
||||
// 再次 tryLock
|
||||
if (TryLock (Self) > 0) {
|
||||
assert (_succ != Self , "invariant") ;
|
||||
assert (_owner == Self , "invariant") ;
|
||||
assert (_Responsible != Self , "invariant") ;
|
||||
return ;
|
||||
}
|
||||
}
|
||||
|
||||
for (;;) {
|
||||
// 本段代码的主要思想和 AQS 中相似可以类比来看
|
||||
// 再次尝试
|
||||
if (TryLock (Self) > 0) break ;
|
||||
assert (_owner != Self, "invariant") ;
|
||||
|
||||
if ((SyncFlags & 2) && _Responsible == NULL) {
|
||||
Atomic::cmpxchg_ptr (Self, &_Responsible, NULL) ;
|
||||
}
|
||||
|
||||
// 满足条件则 park self
|
||||
if (_Responsible == Self || (SyncFlags & 1)) {
|
||||
TEVENT (Inflated enter - park TIMED) ;
|
||||
Self->_ParkEvent->park ((jlong) RecheckInterval) ;
|
||||
// Increase the RecheckInterval, but clamp the value.
|
||||
RecheckInterval *= 8 ;
|
||||
if (RecheckInterval > 1000) RecheckInterval = 1000 ;
|
||||
} else {
|
||||
TEVENT (Inflated enter - park UNTIMED) ;
|
||||
// 通过 park 将当前线程挂起，等待被唤醒
|
||||
Self->_ParkEvent->park() ;
|
||||
}
|
||||
|
||||
if (TryLock(Self) > 0) break ;
|
||||
// 再次尝试自旋
|
||||
if ((Knob_SpinAfterFutile & 1) && TrySpin(Self) > 0) break;
|
||||
}
|
||||
return ;
|
||||
}
|
||||
```
|
||||
|
||||
### monitor 释放
|
||||
|
||||
> 当某个持有锁的线程执行完同步代码块时，会释放锁并 `unpark` 后续线程（由于篇幅只保留重要代码）。
|
||||
|
||||
```java
|
||||
void ATTR ObjectMonitor::exit(bool not_suspended, TRAPS) {
|
||||
Thread * Self = THREAD ;
|
||||
|
||||
if (_recursions != 0) {
|
||||
_recursions--; // this is simple recursive enter
|
||||
TEVENT (Inflated exit - recursive) ;
|
||||
return ;
|
||||
}
|
||||
|
||||
ObjectWaiter * w = NULL ;
|
||||
int QMode = Knob_QMode ;
|
||||
|
||||
// 直接绕过 EntryList 队列，从 cxq 队列中获取线程用于竞争锁
|
||||
if (QMode == 2 && _cxq != NULL) {
|
||||
w = _cxq ;
|
||||
assert (w != NULL, "invariant") ;
|
||||
assert (w->TState == ObjectWaiter::TS_CXQ, "Invariant") ;
|
||||
ExitEpilog (Self, w) ;
|
||||
return ;
|
||||
}
|
||||
// cxq 队列插入 EntryList 尾部
|
||||
if (QMode == 3 && _cxq != NULL) {
|
||||
w = _cxq ;
|
||||
for (;;) {
|
||||
assert (w != NULL, "Invariant") ;
|
||||
ObjectWaiter * u = (ObjectWaiter *) Atomic::cmpxchg_ptr (NULL, &_cxq, w) ;
|
||||
if (u == w) break ;
|
||||
w = u ;
|
||||
}
|
||||
ObjectWaiter * q = NULL ;
|
||||
ObjectWaiter * p ;
|
||||
for (p = w ; p != NULL ; p = p->_next) {
|
||||
guarantee (p->TState == ObjectWaiter::TS_CXQ, "Invariant") ;
|
||||
p->TState = ObjectWaiter::TS_ENTER ;
|
||||
p->_prev = q ;
|
||||
q = p ;
|
||||
}
|
||||
|
||||
ObjectWaiter * Tail ;
|
||||
for (Tail = _EntryList ; Tail != NULL && Tail->_next != NULL ; Tail = Tail->_next) ;
|
||||
if (Tail == NULL) {
|
||||
_EntryList = w ;
|
||||
} else {
|
||||
Tail->_next = w ;
|
||||
w->_prev = Tail ;
|
||||
}
|
||||
}
|
||||
|
||||
// cxq 队列插入到_EntryList 头部
|
||||
if (QMode == 4 && _cxq != NULL) {
|
||||
// 把 cxq 队列放入 EntryList
|
||||
// 此策略确保最近运行的线程位于 EntryList 的头部
|
||||
w = _cxq ;
|
||||
for (;;) {
|
||||
assert (w != NULL, "Invariant") ;
|
||||
ObjectWaiter * u = (ObjectWaiter *) Atomic::cmpxchg_ptr (NULL, &_cxq, w) ;
|
||||
if (u == w) break ;
|
||||
w = u ;
|
||||
}
|
||||
assert (w != NULL , "invariant") ;
|
||||
|
||||
ObjectWaiter * q = NULL ;
|
||||
ObjectWaiter * p ;
|
||||
for (p = w ; p != NULL ; p = p->_next) {
|
||||
guarantee (p->TState == ObjectWaiter::TS_CXQ, "Invariant") ;
|
||||
p->TState = ObjectWaiter::TS_ENTER ;
|
||||
p->_prev = q ;
|
||||
q = p ;
|
||||
}
|
||||
|
||||
if (_EntryList != NULL) {
|
||||
q->_next = _EntryList ;
|
||||
_EntryList->_prev = q ;
|
||||
}
|
||||
_EntryList = w ;
|
||||
}
|
||||
|
||||
w = _EntryList ;
|
||||
if (w != NULL) {
|
||||
assert (w->TState == ObjectWaiter::TS_ENTER, "invariant") ;
|
||||
ExitEpilog (Self, w) ;
|
||||
return ;
|
||||
}
|
||||
w = _cxq ;
|
||||
if (w == NULL) continue ;
|
||||
|
||||
for (;;) {
|
||||
assert (w != NULL, "Invariant") ;
|
||||
ObjectWaiter * u = (ObjectWaiter *) Atomic::cmpxchg_ptr (NULL, &_cxq, w) ;
|
||||
if (u == w) break ;
|
||||
w = u ;
|
||||
}
|
||||
|
||||
if (QMode == 1) {
|
||||
// QMode == 1 : 把 cxq 倾倒入 EntryList 逆序
|
||||
ObjectWaiter * s = NULL ;
|
||||
ObjectWaiter * t = w ;
|
||||
ObjectWaiter * u = NULL ;
|
||||
while (t != NULL) {
|
||||
guarantee (t->TState == ObjectWaiter::TS_CXQ, "invariant") ;
|
||||
t->TState = ObjectWaiter::TS_ENTER ;
|
||||
u = t->_next ;
|
||||
t->_prev = u ;
|
||||
t->_next = s ;
|
||||
s = t;
|
||||
t = u ;
|
||||
}
|
||||
_EntryList = s ;
|
||||
assert (s != NULL, "invariant") ;
|
||||
} else {
|
||||
// QMode == 0 or QMode == 2
|
||||
_EntryList = w ;
|
||||
ObjectWaiter * q = NULL ;
|
||||
ObjectWaiter * p ;
|
||||
// 将单向链表构造成双向环形链表；
|
||||
for (p = w ; p != NULL ; p = p->_next) {
|
||||
guarantee (p->TState == ObjectWaiter::TS_CXQ, "Invariant") ;
|
||||
p->TState = ObjectWaiter::TS_ENTER ;
|
||||
p->_prev = q ;
|
||||
q = p ;
|
||||
}
|
||||
}
|
||||
|
||||
if (_succ != NULL) continue;
|
||||
|
||||
w = _EntryList ;
|
||||
if (w != NULL) {
|
||||
guarantee (w->TState == ObjectWaiter::TS_ENTER, "invariant") ;
|
||||
ExitEpilog (Self, w) ;
|
||||
return ;
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### notify 唤醒
|
||||
|
||||
> notify 或者 notifyAll 方法可以唤醒同一个锁监视器下调用 wait 挂起的线程，具体实现如下
|
||||
|
||||
```java
|
||||
void ObjectMonitor::notify(TRAPS) {
|
||||
CHECK_OWNER();
|
||||
if (_WaitSet == NULL) {
|
||||
TEVENT (Empty - Notify);
|
||||
return;
|
||||
}
|
||||
DTRACE_MONITOR_PROBE(notify, this, object(), THREAD);
|
||||
|
||||
int Policy = Knob_MoveNotifyee;
|
||||
|
||||
Thread::SpinAcquire(&_WaitSetLock, "WaitSet - notify");
|
||||
ObjectWaiter *iterator = DequeueWaiter();
|
||||
if (iterator != NULL) {
|
||||
// 省略一些代码
|
||||
|
||||
// 头插 EntryList
|
||||
if (Policy == 0) {
|
||||
if (List == NULL) {
|
||||
iterator->_next = iterator->_prev = NULL;
|
||||
_EntryList = iterator;
|
||||
} else {
|
||||
List->_prev = iterator;
|
||||
iterator->_next = List;
|
||||
iterator->_prev = NULL;
|
||||
_EntryList = iterator;
|
||||
}
|
||||
} else if (Policy == 1) { // 尾插 EntryList
|
||||
if (List == NULL) {
|
||||
iterator->_next = iterator->_prev = NULL;
|
||||
_EntryList = iterator;
|
||||
} else {
|
||||
ObjectWaiter *Tail;
|
||||
for (Tail = List; Tail->_next != NULL; Tail = Tail->_next);
|
||||
assert (Tail != NULL && Tail->_next == NULL, "invariant");
|
||||
Tail->_next = iterator;
|
||||
iterator->_prev = Tail;
|
||||
iterator->_next = NULL;
|
||||
}
|
||||
} else if (Policy == 2) { // 头插 cxq
|
||||
// prepend to cxq
|
||||
if (List == NULL) {
|
||||
iterator->_next = iterator->_prev = NULL;
|
||||
_EntryList = iterator;
|
||||
} else {
|
||||
iterator->TState = ObjectWaiter::TS_CXQ;
|
||||
for (;;) {
|
||||
ObjectWaiter *Front = _cxq;
|
||||
iterator->_next = Front;
|
||||
if (Atomic::cmpxchg_ptr(iterator, &_cxq, Front) == Front) {
|
||||
break;
|
||||
}
|
||||
}
|
||||
}
|
||||
} else if (Policy == 3) { // 尾插 cxq
|
||||
iterator->TState = ObjectWaiter::TS_CXQ;
|
||||
for (;;) {
|
||||
ObjectWaiter *Tail;
|
||||
Tail = _cxq;
|
||||
if (Tail == NULL) {
|
||||
iterator->_next = NULL;
|
||||
if (Atomic::cmpxchg_ptr(iterator, &_cxq, NULL) == NULL) {
|
||||
break;
|
||||
}
|
||||
} else {
|
||||
while (Tail->_next != NULL) Tail = Tail->_next;
|
||||
Tail->_next = iterator;
|
||||
iterator->_prev = Tail;
|
||||
iterator->_next = NULL;
|
||||
break;
|
||||
}
|
||||
}
|
||||
} else {
|
||||
ParkEvent *ev = iterator->_event;
|
||||
iterator->TState = ObjectWaiter::TS_RUN;
|
||||
OrderAccess::fence();
|
||||
ev->unpark();
|
||||
}
|
||||
|
||||
if (Policy < 4) {
|
||||
iterator->wait_reenter_begin(this);
|
||||
}
|
||||
}
|
||||
// 自旋释放
|
||||
Thread::SpinRelease(&_WaitSetLock);
|
||||
|
||||
if (iterator != NULL && ObjectMonitor::_sync_Notifications != NULL) {
|
||||
ObjectMonitor::_sync_Notifications->inc();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
## 总结
|
||||
|
||||
本文介绍了 `synchronized` 工作原理和锁升级的过程。其中锁队列的协作流程较复杂，本文配了详细的流程图可以参照。最后附上了一部分重要代码的解析，理解 `synchronized` 原理之后便于写出性能更高的代码。
|
||||
|
||||
简单的来说偏向锁通过对比 Mark Word thread id 解决加锁问题。而轻量级锁是通过用 CAS 操作 Mark Word 和自旋来解决加锁问题，避免线程阻塞和唤醒而影响性能。重量级锁是将除了拥有锁的线程以外的线程都阻塞。
|
||||
|
||||
## 参考资料
|
||||
|
||||
- [HotSpot Glossary of Terms](http://openjdk.java.net/groups/hotspot/docs/HotSpotGlossary.html)
|
||||
- [Java SE 6 Performance White Paper](https://www.oracle.com/technetwork/java/6-performance-137236.html)
|
||||
Loading…
Reference in New Issue
Block a user