12 KiB
알고리즘 - 자바
이 개발브런치는 기존 프로젝트를 Java 프로젝트 구조로 재개발하기 위해 작성되었다. 기여도를 위해 개발 지사로 전환할 수 있다. 자세한 내용은 이 문제를 참조하십시오. 컨트리뷰션을 위해 개발브런치로 전환할 수 있다. 자세한 내용은 이 이슈를 참고하십시오.
자바로 구현된 모든 알고리즘들 (교육용)
이것들은 단지 시범을 위한 것이다. 표준 자바 라이브러리에는 성능상의 이유로 더 나은 것들이 구현되어있다
정렬 알고리즘
Bubble(버블 정렬)
From Wikipedia: 버블 소트(sinking sor라고도 불리움)는 리스트를 반복적인 단계로 접근하여 정렬한다. 각각의 짝을 비교하며, 순서가 잘못된 경우 그접한 아이템들을 스왑하는 알고리즘이다. 더 이상 스왑할 것이 없을 때까지 반복하며, 반복이 끝남음 리스트가 정렬되었음을 의미한다.
속성
- 최악의 성능 O(n^2)
- 최고의 성능 O(n)
- 평균 성능 O(n^2)
View the algorithm in action
Insertion(삽입 정렬)
From Wikipedia: 삽입 정렬은 최종 정렬된 배열(또는 리스트)을 한번에 하나씩 구축하는 알고리즘이다. 이것은 큰 리스트에서 더 나은 알고리즘인 퀵 소트, 힙 소트, 또는 머지 소트보다 훨씬 안좋은 효율을 가진다. 그림에서 각 막대는 정렬해야 하는 배열의 요소를 나타낸다. 상단과 두 번째 상단 막대의 첫 번째 교차점에서 발생하는 것은 두 번째 요소가 첫 번째 요소보다 더 높은 우선 순위를 가지기 떄문에 막대로 표시되는 이러한 요소를 교환한 것이다. 이 방법을 반복하면 삽입 정렬이 완료된다.
속성
- 최악의 성능 O(n^2)
- 최고의 성능 O(n)
- 평균 O(n^2)
View the algorithm in action
Merge(합병 정렬)
From Wikipedia: 컴퓨터 과학에서, 합병 정렬은 효율적인, 범용적인, 비교 기반 정렬 알고리즘이다. 대부분의 구현은 안정적인 분류를 이루는데, 이것은 구현이 정렬된 출력에 동일한 요소의 입력 순서를 유지한다는 것을 의미한다. 합병 정렬은 1945년에 John von Neumann이 발명한 분할 정복 알고리즘이다.
속성
- 최악의 성능 O(n log n) (일반적)
- 최고의 성능 O(n log n)
- 평균 O(n log n)
View the algorithm in action
Quick(퀵 정렬)
From Wikipedia: 퀵 정렬sometimes called partition-exchange sort)은 효율적인 정렬 알고리즘으로, 배열의 요소를 순서대로 정렬하는 체계적인 방법 역활을 한다.
속성
- 최악의 성능 O(n^2)
- 최고의 성능 O(n log n) or O(n) with three-way partition
- 평균 O(n log n)
View the algorithm in action
Selection(선택 정렬)
From Wikipedia: 알고리즘 입력 리스트를 두 부분으로 나눈다 : 첫 부분은 아이템들이 이미 왼쪽에서 오른쪽으로 정렬되었다. 그리고 남은 부분의 아이템들은 나머지 항목을 차지하는 리스트이다. 처음에는 정렬된 리스트는 공백이고 나머지가 전부이다. 오르차순(또는 내림차순) 알고리즘은 가장 작은 요소를 정렬되지 않은 리스트에서 찾고 정렬이 안된 가장 왼쪽(정렬된 리스트) 리스트와 바꾼다. 이렇게 오른쪽으로 나아간다.
속성
- 최악의 성능 O(n^2)
- Best case performance O(n^2)
- Average case performance O(n^2)
View the algorithm in action
Shell
From Wikipedia: Shellsort is a generalization of insertion sort that allows the exchange of items that are far apart. The idea is to arrange the list of elements so that, starting anywhere, considering every nth element gives a sorted list. Such a list is said to be h-sorted. Equivalently, it can be thought of as h interleaved lists, each individually sorted.
Properties
- Worst case performance O(nlog2 2n)
- Best case performance O(n log n)
- Average case performance depends on gap sequence
View the algorithm in action
Time-Compexity Graphs
Comparing the complexity of sorting algorithms (Bubble Sort, Insertion Sort, Selection Sort)
Search Algorithms
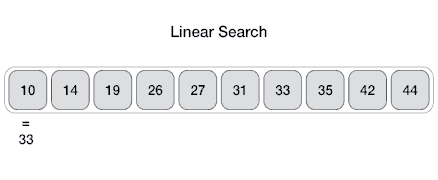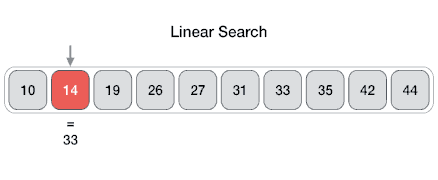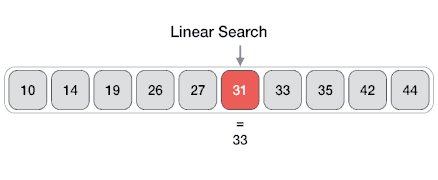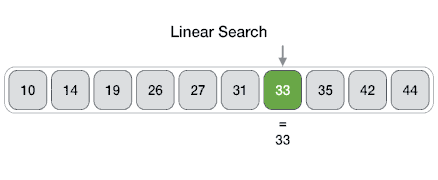
Linear
From Wikipedia: linear search or sequential search is a method for finding a target value within a list. It sequentially checks each element of the list for the target value until a match is found or until all the elements have been searched. The linear search runs in at the worst linear time and makes at most n comparisons, where n is the length of the list.
Properties
- Worst case performance O(n)
- Best case performance O(1)
- Average case performance O(n)
- Worst case space complexity O(1) iterative
Binary
From Wikipedia: Binary search, also known as half-interval search or logarithmic search, is a search algorithm that finds the position of a target value within a sorted array. It compares the target value to the middle element of the array; if they are unequal, the half in which the target cannot lie is eliminated and the search continues on the remaining half until it is successful.
Properties
- Worst case performance O(log n)
- Best case performance O(1)
- Average case performance O(log n)
- Worst case space complexity O(1)
From Wikipedia: Shellsort is a generalization of insertion sort that allows the exchange of items that are far apart. The idea is to arrange the list of elements so that, starting anywhere, considering every nth element gives a sorted list. Such a list is said to be h-sorted. Equivalently, it can be thought of as h interleaved lists, each individually sorted.
Properties
- Worst case performance O(nlog2 2n)
- Best case performance O(n log n)
- Average case performance depends on gap sequence
View the algorithm in action
Links to the rest of the algorithms
| Conversions | Dynamic Programming | Ciphers | Miscellaneous |
|---|---|---|---|
| Any Base to Any Base | Coin Change | Caesar | Heap Sort |
| Any Base to Decimal | Egg Dropping | Columnar Transposition Cipher | Palindromic Prime Checker |
| Binary to Decimal | Fibonacci | RSA | More soon... |
| Binary to HexaDecimal | Kadane Algorithm | more coming soon... | |
| Binary to Octal | Knapsack | ||
| Decimal To Any Base | Longest Common Subsequence | ||
| Decimal To Binary | Longest Increasing Subsequence | ||
| Decimal To Hexadecimal | Rod Cutting | ||
| and much more... | and more... |
Data Structures
| Graphs | Heaps | Lists | Queues |
|---|---|---|---|
| BFS | Empty Heap Exception | Circle Linked List | Generic Array List Queue |
| DFS | Heap | Doubly Linked List | Queues |
| Graphs | Heap Element | Singly Linked List | |
| Kruskals Algorithm | Max Heap | ||
| Matrix Graphs | Min Heap | ||
| PrimMST |
| Stacks | Trees |
|---|---|
| Node Stack | AVL Tree |
| Stack of Linked List | Binary Tree |
| Stacks | And much more... |