@ -1,6 +1,8 @@
|
||||
## LeetCode第11号问题:盛水最多的容器
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步个人博客:https://www.zhangxiaoshuai.fun
|
||||
> 同步个人博客:www.zhangxiaoshuai.fun
|
||||
|
||||
**本题选自leetcode的第11题,medium级别,目前通过率:61.3%**
|
||||
|
||||
|
||||
|
After Width: | Height: | Size: 6.6 MiB |
149
0022-Generate-Parentheses/Article/0022-Generate-Parentheses.md
Normal file
@ -0,0 +1,149 @@
|
||||
# LeetCode 第 22 号问题:生成所有的括号对
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
题目来源于 LeetCode 上第 22 号问题:生成所有的括号对。题目难度为 Medium,目前通过率为 60.9% 。
|
||||
|
||||
### 题目描述
|
||||
|
||||
给定数字n,要求使用n对()括号生成所有合法的组合情况。
|
||||
|
||||
**示例**
|
||||
|
||||
```
|
||||
3
|
||||
|
||||
[
|
||||
"((()))",
|
||||
"(()())",
|
||||
"(())()",
|
||||
"()(())",
|
||||
"()()()"
|
||||
]
|
||||
```
|
||||
|
||||
### 题目解析
|
||||
|
||||
#### 解法一: 暴力
|
||||
|
||||
暴力的解法应该最容易想到,因为n是确定的,也就是说一共有n个左括号和n个右括号。很容易想到,我们可以对这2n个字符进行排列组合,之后再对所有的组合进行过滤。留下合法的且不重复的即可。
|
||||
|
||||
伪代码很容易写:
|
||||
|
||||
```python
|
||||
def brute_force(str, l, r):
|
||||
if l == n and r == n:
|
||||
ans.append(str)
|
||||
if l < n:
|
||||
brute_force(str+'(', l+1, r)
|
||||
if r < n:
|
||||
brute_force(str+')', l, r+1)
|
||||
```
|
||||
|
||||
写完了再根据结果判断是否合法,留下合法的所有情况即可。
|
||||
|
||||
这样编码的确不难,而且也很容易想到,但是计算n个字符的排列组合复杂度是 $O(2^n)$ 是一个指数级的算法,复杂度是我们不能接受的。而且根据上一题当中的结论,在匹配括号的时候是可以取巧的,我们其实没必要把所有的情况都枚举到。因为想要括号匹配合法,必须有一条,对于字符串当中的任何一个位置i,都必须有:前i个字符中所有左括号的数量大于等于右括号的数量。
|
||||
,否则就是非法的。
|
||||
|
||||
也就是说必须要保证任意一个位置右括号的数量小于等于左括号的数量,不然的话,多余的右括号永远也无法匹配。
|
||||
|
||||
#### 解法二: 回溯
|
||||
|
||||
既然左括号的数量必须大于右括号的数量,我们完全可以据此进行优化。我们在递归的时候对l和r进行大小判断,保证所有时刻都有l >= r即可。
|
||||
|
||||
代码:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
|
||||
void dfs(int n, int l, int r, string str, vector<string>& vt) {
|
||||
if (l+r == 2 *n) {
|
||||
vt.push_back(str);
|
||||
return ;
|
||||
}
|
||||
if (l < n) dfs(n, l+1, r, str+"(", vt);
|
||||
if (r < l) dfs(n, l, r+1, str+")", vt);
|
||||
}
|
||||
|
||||
vector<string> generateParenthesis(int n) {
|
||||
vector<string> vt;
|
||||
dfs(n, 0, 0, "", vt);
|
||||
return vt;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
#### 解法三: 构造
|
||||
|
||||
这个方法是我原创的,官方的题解当中没有收录。
|
||||
|
||||
我们直接求解n的答案的时候是比较困难的,这个时候我们可以把问题拆解,大问题变成小问题,通过小问题的答案构造大问题的答案。上述的两种方法本质上也是一样的思路,不过递归替我们做了问题的拆分。
|
||||
|
||||
实际上我们可以自己拆分问题,n的时候我们一下子不清楚答案。我们可以先从简单的观察一下结果:比如当n==1的时候,答案就是”()”。n==2有两种:”()()”, “(())”。n==3的时候是5种:”((()))”, “()(())”, “()()()”, “(()())”, “(())()”。
|
||||
|
||||
细心的读者已经可以总结出规律了,其实并不难想到。
|
||||
|
||||
solution(n) = solution(i) + solution(n-i) + '(' solution(n-1) ')'
|
||||
|
||||
解释一下这个公式,这里的solution(n)表示n的所有答案串,也就是说n个括号的答案串是可以通过小于n的答案串进行组合的。比如n=1时答案是(),n=2则有两种,一种是用两个n=1拼接,第二种是在n=1的答案外层加上一个括号:
|
||||
|
||||
solution(2) = [()(), (())]
|
||||
|
||||
我们再来看solution(3),它可以用n=1和n=2拼接,以及通过n=2外层加上单独的括号得到所有答案:
|
||||
|
||||
solution(3) = [()()(), ()(()), (())(), (()()), ((()))]
|
||||
|
||||
前面3种是通过solution(2)和solution(1)拼接得到的,后面两种则是在solution(2)外面直接加上括号得到的,这种情况是无法通过拼接得到的情况。我们把这些情况全部汇总,然后去除掉重复的情况就是答案了。
|
||||
|
||||
这样我们就用小于n的所有结果构造出了n的结果,由于n=0 和n=1的情况是已知的。我们只需要把中间结果存储下来,通过递推就可以获取所有的答案。
|
||||
|
||||
### 动画描述
|
||||
|
||||

|
||||
|
||||
### 代码实现
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
|
||||
vector<string> generateParenthesis(int n) {
|
||||
// 存储所有中间结果
|
||||
map<int, set<string>> mp;
|
||||
set<string> st;
|
||||
st.insert("()");
|
||||
mp[1] = st;
|
||||
|
||||
for (int i = 2; i <= n; i++) {
|
||||
// 使用set来去重
|
||||
set<string> cur;
|
||||
for (int j = 1; j <= i-1; j++) {
|
||||
// 取出所有solution(j)和solution(i-j)
|
||||
set<string> vj = mp[j];
|
||||
set<string> vk = mp[i-j];
|
||||
for (string str:vj) {
|
||||
for (string stj : vk) {
|
||||
cur.insert(str + stj);
|
||||
}
|
||||
}
|
||||
}
|
||||
// solution(i-1)最外层套上括号
|
||||
set<string> vj = mp[i-1];
|
||||
for (string str : vj) {
|
||||
cur.insert("(" + str + ")");
|
||||
}
|
||||
// 得到solution(i)
|
||||
mp[i] = cur;
|
||||
}
|
||||
vector<string> vt;
|
||||
st = mp[n];
|
||||
for (string str : st) vt.push_back(str);
|
||||
return vt;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||

|
||||
BIN
0024-Swap-Nodes-in-Pairs/Animation/Animation1.gif
Normal file
|
After Width: | Height: | Size: 4.7 MiB |
BIN
0024-Swap-Nodes-in-Pairs/Animation/Animation2.gif
Normal file
|
After Width: | Height: | Size: 2.4 MiB |
128
0024-Swap-Nodes-in-Pairs/Article/0024-Swap-Nodes-in-Pairs2.md
Normal file
@ -0,0 +1,128 @@
|
||||
# LeetCode 第 24 号问题:两两交换链表中的节点
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
题目来源于 LeetCode 上第 24 号问题:两两交换链表中的节点。
|
||||
|
||||
### 题目描述
|
||||
|
||||
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
|
||||
|
||||
**你不能只是单纯的改变节点内部的值**,而是需要实际的进行节点交换。
|
||||
|
||||
**示例:**
|
||||
|
||||
```
|
||||
给定 1->2->3->4, 你应该返回 2->1->4->3.
|
||||
```
|
||||
|
||||
### 题目解析 - 迭代法
|
||||
|
||||
由题目描述可知需要两两交换, 那么以两个为一组子链表交换指针即可, 在设置一个 **哨兵** 指向交换后的子链表 (或者哨兵提前指向子链表的第二个节点,因为第二个节点交换后就成了第一个节点); 然后让哨兵指向下一组子链表,继续交换,直至最后.
|
||||
|
||||
设 **哨兵** 为 节点 `prev`, 子链表第一个节点为 `A`, 第二个节点为 `B`, 第三个节点为 `C`, 那么操作流程如下:
|
||||
|
||||
- 终止条件 `head == null && head -> next == null`
|
||||
1. prev -> B ( A -> B -> C )
|
||||
2. A - > C
|
||||
3. B -> A ( prev -> B -> A -> C )
|
||||
4. prev -> A
|
||||
5. head -> C
|
||||
6. 循环以上步骤
|
||||
|
||||
### 动画描述
|
||||
|
||||
<img src="../Animation/Animation1.gif" alt="Animation1" style="zoom:150%;" />
|
||||
|
||||
### 代码实现
|
||||
|
||||
```javascript
|
||||
/**
|
||||
* JavaScript描述
|
||||
* 迭代法
|
||||
*/
|
||||
var swapPairs = function(head) {
|
||||
let dummy = new ListNode(0);
|
||||
dummy.next = head;
|
||||
|
||||
let prevNode = dummy;
|
||||
|
||||
while (head !== null && head.next !== null) {
|
||||
// Nodes to be swapped
|
||||
let firstNode = head,
|
||||
secondNode = head.next;
|
||||
// Swapping
|
||||
prevNode.next = secondNode; // 放到交换前后都可以
|
||||
firstNode.next = secondNode.next;
|
||||
secondNode.next = firstNode;
|
||||
// Reinitializing the head and prevNode for next swap
|
||||
prevNode = firstNode;
|
||||
head = firstNode.next;
|
||||
}
|
||||
return dummy.next;
|
||||
};
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
- 时间复杂度:**O(N)**,其中 *N* 指的是链表的节点数量
|
||||
- 空间复杂度:**O(1)**
|
||||
|
||||
### 题目解析 - 递归
|
||||
|
||||
递归的思路和迭代类似, 都是分组交换. 具体来说这里的递归不是针对一个问题深入进去,而是不断向后推进.
|
||||
|
||||
- 每次递归只交换一对节点
|
||||
- 下一次递归则是交换下一对节点
|
||||
- 交换完成后返回第二个节点, 因为它是交换后的子链表新头
|
||||
- 递归完成后返回第一次递归的第二个节点, 这就是新链表的头结点
|
||||
|
||||
**注意:** 不要人肉递归, 更多关注整体逻辑
|
||||
|
||||
示例执行大致流程为:
|
||||
|
||||
- 终止条件: `(head == null) || (head.next == null)`
|
||||
1. 1 -> 2 -> 3 -> 4 ( 原始链表 )
|
||||
2. 1 -> 3 -> 4
|
||||
3. ( 2 -> 1 ) -> 3 -> 4 ( 第一次递归完成后返回原来的第二个节点, 也就是值为 2 的节点 )
|
||||
4. 2 -> 1 -> 3 -> null
|
||||
5. 2 -> 1 -> ( 4 -> 3 ) ( 第二次递归完成后返回原来的第二个节点, 也就是值为 4 的节点 )
|
||||
|
||||
### 动画描述
|
||||
|
||||
<img src="../Animation/Animation2.gif" alt="Animation2" style="zoom:150%;" />
|
||||
|
||||
### 代码实现
|
||||
|
||||
```javascript
|
||||
/**
|
||||
* JavaScript描述
|
||||
* 递归法
|
||||
*/
|
||||
var swapPairs = function(head) {
|
||||
if (head == null || head.next == null) {
|
||||
return head;
|
||||
}
|
||||
// Nodes to be swapped
|
||||
let firstNode = head,
|
||||
secondNode = head.next;
|
||||
// Swapping
|
||||
firstNode.next = swapPairs(secondNode.next);
|
||||
secondNode.next = firstNode;
|
||||
|
||||
return secondNode;
|
||||
|
||||
};
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
- 时间复杂度:**O(N)**,其中 *N* 指的是链表的节点数量
|
||||
- 空间复杂度:**O(N)**, 递归过程使用的堆栈空间
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
|
After Width: | Height: | Size: 6.5 MiB |
@ -0,0 +1,81 @@
|
||||
# LeetCode 第 34 号问题:在排序数组中查找元素的第一个和最后一个位置
|
||||
|
||||
|
||||
题目来源于 LeetCode 上第 34 号问题:find-first-and-last-position-of-element-in-sorted-array。题目难度为 中等。
|
||||
|
||||
### 题目描述
|
||||
|
||||
给定一个按照升序排列的整数数组 **nums**,和一个目标值 **target**。找出给定目标值在数组中的开始位置和结束位置。
|
||||
|
||||
你的算法时间复杂度必须是 **O(log n)** 级别。
|
||||
|
||||
如果数组中不存在目标值,返回 [-1, -1]。
|
||||
|
||||
|
||||
**示例:**
|
||||
|
||||
```
|
||||
输入: nums = [5,7,7,8,8,10], target = 8
|
||||
输出: [3,4]
|
||||
```
|
||||
```
|
||||
输入: nums = [5,7,7,8,8,10], target = 6
|
||||
输出: [-1,-1]
|
||||
```
|
||||
### 题目解析
|
||||
|
||||
题目中要求了时间复杂度为O(log n),这就很清楚要使用二分查找法了。
|
||||
|
||||
首先定义两个指针变量,分别存储左右两个位置的索引。首先去找目标值的最左面的索引,通过循环为了防止元素丢失,每次保留最右面的元素,左侧的指针移动时+1。在循环结束的时候判断一下数组中是否包括目标值,不包括的话直接退出。
|
||||
右面的跟左侧相同,只不过正好相反。
|
||||
|
||||
|
||||
|
||||
### 动画描述
|
||||
|
||||

|
||||
|
||||
### 代码实现
|
||||
|
||||
```java
|
||||
// 34. 下一个排列
|
||||
// https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/
|
||||
// 时间复杂度:O(n)
|
||||
// 空间复杂度:O(1)
|
||||
class Solution {
|
||||
public int[] searchRange(int[] nums, int target) {
|
||||
int[] res = new int[] { -1, -1 };
|
||||
int left = 0;
|
||||
int right = nums.length - 1;
|
||||
int l = left;
|
||||
int r = right;
|
||||
while (left < right) {
|
||||
int mid = (left + right) / 2;
|
||||
if (nums[mid] < target) {
|
||||
left = mid + 1;
|
||||
} else {
|
||||
right = mid;
|
||||
}
|
||||
}
|
||||
if (left>right||nums[left]!=target) {
|
||||
return new int[]{-1,-1};
|
||||
}
|
||||
while (l < r) {
|
||||
int mid = (l + r) / 2 + 1;
|
||||
if (nums[mid] > target) {
|
||||
r = mid - 1;
|
||||
} else {
|
||||
l = mid;
|
||||
}
|
||||
}
|
||||
if (left > right || left > r) {
|
||||
return new int[] { -1, -1 };
|
||||
} else {
|
||||
return new int[] { left, r };
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||

|
||||
33
0034-find-first-and-last-position-of-element-in-sorted-array/Code/1.java
Executable file
@ -0,0 +1,33 @@
|
||||
class Solution {
|
||||
public int[] searchRange(int[] nums, int target) {
|
||||
int[] res = new int[] { -1, -1 };
|
||||
int left = 0;
|
||||
int right = nums.length - 1;
|
||||
int l = left;
|
||||
int r = right;
|
||||
while (left < right) {
|
||||
int mid = (left + right) / 2;
|
||||
if (nums[mid] < target) {
|
||||
left = mid + 1;
|
||||
} else {
|
||||
right = mid;
|
||||
}
|
||||
}
|
||||
if (left>right||nums[left]!=target) {
|
||||
return new int[]{-1,-1};
|
||||
}
|
||||
while (l < r) {
|
||||
int mid = (l + r) / 2 + 1;
|
||||
if (nums[mid] > target) {
|
||||
r = mid - 1;
|
||||
} else {
|
||||
l = mid;
|
||||
}
|
||||
}
|
||||
if (left > right || left > r) {
|
||||
return new int[] { -1, -1 };
|
||||
} else {
|
||||
return new int[] { left, r };
|
||||
}
|
||||
}
|
||||
}
|
||||
BIN
0035-search-insert-position/Animation/~$搜索插入位置.pptx
Executable file
BIN
0035-search-insert-position/Animation/二分查找.gif
Executable file
|
After Width: | Height: | Size: 2.9 MiB |
BIN
0035-search-insert-position/Animation/二分查找.mp4
Executable file
BIN
0035-search-insert-position/Animation/暴力查找.gif
Executable file
|
After Width: | Height: | Size: 2.4 MiB |
BIN
0035-search-insert-position/Animation/暴力查找.mp4
Executable file
113
0035-search-insert-position/Article/0035-search-insert-position.md
Executable file
@ -0,0 +1,113 @@
|
||||
# LeetCode 第 35 号问题:搜索插入位置
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
题目来源于 LeetCode 第 35 号问题:搜索插入位置.
|
||||
|
||||
## 题目
|
||||
|
||||
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
|
||||
你可以假设数组中无重复元素。
|
||||
|
||||
|
||||
示例 1:
|
||||
|
||||
```
|
||||
输入: [1,3,5,6], 5
|
||||
输出: 2
|
||||
```
|
||||
|
||||
示例 2:
|
||||
|
||||
|
||||
```
|
||||
输入: [1,3,5,6], 2
|
||||
输出: 1
|
||||
```
|
||||
|
||||
示例 3:
|
||||
|
||||
|
||||
```
|
||||
输入: [1,3,5,6], 7
|
||||
输出: 4
|
||||
```
|
||||
|
||||
|
||||
示例 4:
|
||||
|
||||
|
||||
```
|
||||
输入: [1,3,5,6], 0
|
||||
输出: 0
|
||||
```
|
||||
|
||||
|
||||
|
||||
## 思路解析
|
||||
|
||||
### 暴力循环法
|
||||
|
||||
这个题看起来就是很简单的,就是一道考验查找算法的题目。最简单的就是暴力查找了。
|
||||
|
||||
#### 思路
|
||||
|
||||
遍历这个数组,然后如果当前值和目标值target一致或小于目标值target,那么就return 当前下标。这种解法的时间复杂度是O(N)
|
||||
|
||||
### 动画理解
|
||||
|
||||

|
||||
|
||||
#### 代码实现
|
||||
|
||||
|
||||
```java
|
||||
//时间复杂度:O(n)
|
||||
//空间复杂度:O(1)
|
||||
class Solution {
|
||||
public int searchInsert(int[] nums, int target) {
|
||||
int i=0;
|
||||
for(;i<nums.length;i++){
|
||||
if (nums[i]>=target){
|
||||
break;
|
||||
}
|
||||
}
|
||||
return i;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### 二分法
|
||||
|
||||
#### 思路
|
||||
|
||||
除了暴力法,我们在排序数组中查找值还可以用的一种方法是二分法,思路还是和改良的暴力循环法一样,先找到左右边界,然后计算,每次可以省出一半的时间。时间复杂度为O(logn)
|
||||
|
||||
#### 代码实现
|
||||
|
||||
```java
|
||||
//时间复杂度:O(lon(n))
|
||||
//空间复杂度:O(1)
|
||||
class Solution {
|
||||
public int searchInsert(int[] nums, int target) {
|
||||
if (target>nums[nums.length-1]) {
|
||||
return nums.length;
|
||||
}
|
||||
int left=0;
|
||||
int right=nums.length-1;
|
||||
while (left < right) {
|
||||
int mid = (left + right) / 2;
|
||||
if (nums[mid] < target) {
|
||||
left = mid + 1;
|
||||
} else {
|
||||
right = mid;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
|
||||
}
|
||||
}
|
||||
```
|
||||

|
||||
11
0035-search-insert-position/Code/1.java
Executable file
@ -0,0 +1,11 @@
|
||||
class Solution1 {
|
||||
public int searchInsert(int[] nums, int target) {
|
||||
int i=0;
|
||||
for(;i<nums.length;i++){
|
||||
if (nums[i]>=target){
|
||||
break;
|
||||
}
|
||||
}
|
||||
return i;
|
||||
}
|
||||
}
|
||||
21
0035-search-insert-position/Code/2.java
Executable file
@ -0,0 +1,21 @@
|
||||
//时间复杂度:O(lon(n))
|
||||
//空间复杂度:O(1)
|
||||
class Solution2 {
|
||||
public int searchInsert(int[] nums, int target) {
|
||||
if (target>nums[nums.length-1]) {
|
||||
return nums.length;
|
||||
}
|
||||
int left=0;
|
||||
int right=nums.length-1;
|
||||
while (left < right) {
|
||||
int mid = (left + right) / 2;
|
||||
if (nums[mid] < target) {
|
||||
left = mid + 1;
|
||||
} else {
|
||||
right = mid;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
|
||||
}
|
||||
}
|
||||
BIN
0036-valid-sudoku/Animation/HashMap.gif
Executable file
|
After Width: | Height: | Size: 5.7 MiB |
BIN
0036-valid-sudoku/Animation/HashMap.mp4
Executable file
134
0036-valid-sudoku/Article/0036-valid-sudoku.md
Executable file
@ -0,0 +1,134 @@
|
||||
# LeetCode 第 36 号问题:有效的数独
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
题目来源于 LeetCode 第 36 号问题:有效的数独.
|
||||
|
||||
## 题目
|
||||
|
||||
判断一个 9x9 的数独是否有效。只需要根据以下规则,验证已经填入的数字是否有效即可。
|
||||
|
||||
|
||||
数字 1-9 在每一行只能出现一次。
|
||||
数字 1-9 在每一列只能出现一次。
|
||||
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
|
||||
|
||||
|
||||
示例 1:
|
||||
|
||||
```
|
||||
输入:
|
||||
[
|
||||
["5","3",".",".","7",".",".",".","."],
|
||||
["6",".",".","1","9","5",".",".","."],
|
||||
[".","9","8",".",".",".",".","6","."],
|
||||
["8",".",".",".","6",".",".",".","3"],
|
||||
["4",".",".","8",".","3",".",".","1"],
|
||||
["7",".",".",".","2",".",".",".","6"],
|
||||
[".","6",".",".",".",".","2","8","."],
|
||||
[".",".",".","4","1","9",".",".","5"],
|
||||
[".",".",".",".","8",".",".","7","9"]
|
||||
]
|
||||
输出: true
|
||||
```
|
||||
|
||||
示例 2:
|
||||
|
||||
|
||||
```
|
||||
输入:
|
||||
[
|
||||
["8","3",".",".","7",".",".",".","."],
|
||||
["6",".",".","1","9","5",".",".","."],
|
||||
[".","9","8",".",".",".",".","6","."],
|
||||
["8",".",".",".","6",".",".",".","3"],
|
||||
["4",".",".","8",".","3",".",".","1"],
|
||||
["7",".",".",".","2",".",".",".","6"],
|
||||
[".","6",".",".",".",".","2","8","."],
|
||||
[".",".",".","4","1","9",".",".","5"],
|
||||
[".",".",".",".","8",".",".","7","9"]
|
||||
]
|
||||
输出: false
|
||||
解释: 除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。
|
||||
但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
|
||||
```
|
||||
|
||||
示例 3:
|
||||
|
||||
|
||||
```
|
||||
输入: [1,3,5,6], 7
|
||||
输出: 4
|
||||
```
|
||||
|
||||
|
||||
示例 4:
|
||||
|
||||
|
||||
```
|
||||
输入: [1,3,5,6], 0
|
||||
输出: 0
|
||||
```
|
||||
|
||||
|
||||
|
||||
## 思路解析
|
||||
|
||||
### 一次遍历法
|
||||
|
||||
#### 思路
|
||||
|
||||
这道题因为需要判断数值是否存在,所以用Hash Map是一个很好的选择。
|
||||
因为每一行、每一列、每一格都是需要单独进行判断的,所以需要建立三个长度为9的HashMap数组,分别存放行、列、格的数值。
|
||||
|
||||
通过一个二层循环遍历这个9*9的数组,把当前格的数值存放到对应的HashMap中,判断之前是否已经存放过了,如果已经存放过那就退出,返回false,如果是.的话那就跳过,这样只需要遍历一边就可以了。
|
||||
|
||||
### 动画理解
|
||||
|
||||

|
||||
|
||||
#### 代码实现
|
||||
|
||||
|
||||
```java
|
||||
//时间复杂度:O(n)
|
||||
//空间复杂度:O(1)
|
||||
class Solution {
|
||||
public boolean isValidSudoku(char[][] board) {
|
||||
HashMap[] row = new HashMap[9];
|
||||
HashMap[] column = new HashMap[9];
|
||||
HashMap[] box = new HashMap[9];
|
||||
for (int i = 0; i < 9; i++) {
|
||||
row[i] = new HashMap(9);
|
||||
column[i] = new HashMap(9);
|
||||
box[i] = new HashMap(9);
|
||||
}
|
||||
for (int i = 0; i < 9; i++) {
|
||||
for (int j = 0; j < 9; j++) {
|
||||
if (board[i][j] == '.') {
|
||||
continue;
|
||||
}
|
||||
int boxIndex=i / 3 * 3 + j / 3;
|
||||
if ((boolean) row[i].getOrDefault(board[i][j], true)) {
|
||||
return false;
|
||||
}
|
||||
if ((boolean) column[j].getOrDefault(board[i][j], true)) {
|
||||
return false;
|
||||
}
|
||||
if ((boolean) box[boxIndex].getOrDefault(board[i][j], true)) {
|
||||
return false;
|
||||
}
|
||||
row[i].put(board[i][j], false);
|
||||
column[j].put(board[i][j], false);
|
||||
box[boxIndex].put(board[i][j], false);
|
||||
}
|
||||
}
|
||||
|
||||
return true;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
34
0036-valid-sudoku/Code/1.java
Executable file
@ -0,0 +1,34 @@
|
||||
class Solution {
|
||||
public boolean isValidSudoku(char[][] board) {
|
||||
HashMap[] row = new HashMap[9];
|
||||
HashMap[] column = new HashMap[9];
|
||||
HashMap[] box = new HashMap[9];
|
||||
for (int i = 0; i < 9; i++) {
|
||||
row[i] = new HashMap(9);
|
||||
column[i] = new HashMap(9);
|
||||
box[i] = new HashMap(9);
|
||||
}
|
||||
for (int i = 0; i < 9; i++) {
|
||||
for (int j = 0; j < 9; j++) {
|
||||
if (board[i][j] == '.') {
|
||||
continue;
|
||||
}
|
||||
int boxIndex=i / 3 * 3 + j / 3;
|
||||
if ((boolean) row[i].getOrDefault(board[i][j], true)) {
|
||||
return false;
|
||||
}
|
||||
if ((boolean) column[j].getOrDefault(board[i][j], true)) {
|
||||
return false;
|
||||
}
|
||||
if ((boolean) box[boxIndex].getOrDefault(board[i][j], true)) {
|
||||
return false;
|
||||
}
|
||||
row[i].put(board[i][j], false);
|
||||
column[j].put(board[i][j], false);
|
||||
box[boxIndex].put(board[i][j], false);
|
||||
}
|
||||
}
|
||||
|
||||
return true;
|
||||
}
|
||||
}
|
||||
BIN
0042-Trap/Animation/0042-Trap.gif
Normal file
|
After Width: | Height: | Size: 7.3 MiB |
BIN
0042-Trap/Animation/01.png
Normal file
|
After Width: | Height: | Size: 7.5 KiB |
BIN
0042-Trap/Animation/02.png
Normal file
|
After Width: | Height: | Size: 7.9 KiB |
BIN
0042-Trap/Animation/03.png
Normal file
|
After Width: | Height: | Size: 7.9 KiB |
BIN
0042-Trap/Animation/resource.png
Normal file
|
After Width: | Height: | Size: 7.7 KiB |
136
0042-Trap/Article/0042-Trap.md
Normal file
@ -0,0 +1,136 @@
|
||||
## LeetCode第42号问题:接雨水
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 个人博客:www.zhangxiaoshuai.fun
|
||||
|
||||
**本题选择leetcode中第42题,hard级别,目前通过率50.8%#**
|
||||
|
||||
### 题目描述:
|
||||
|
||||
```txt
|
||||
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
|
||||
示例:
|
||||
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
|
||||
输出: 6
|
||||
```
|
||||
|
||||

|
||||
|
||||
### 题目分析:
|
||||
|
||||
通过题意,一个“凹槽”可以存储的雨水的容量取决于它前后的柱子。
|
||||
|
||||
### 解法一:
|
||||
|
||||
仔细想想,其实这跟木桶原理是有相似的地方的,针对每一个柱子,我们需要往前看和往后看,分别找出当前柱子前面最高的柱子和后面最高的柱子。
|
||||
|
||||
这里有**三种情况**我们需要了解:
|
||||
|
||||
- **当前柱子小于前后两个柱子中最矮的那个**
|
||||

|
||||
|
||||
**当前位置可以存储的雨水容量 = leftMax - curr = 1**
|
||||
|
||||
|
||||
|
||||
- **当前柱子等于前后两个柱子中最矮的那个**
|
||||

|
||||
|
||||
**当前位置可以存储的雨水容量为0**
|
||||
|
||||
|
||||
|
||||
- **当前柱子大于前后两个柱子中最矮的那个**
|
||||
|
||||
**因为curr < leftMax,所以当前位置无法存储雨水**
|
||||
|
||||
**GIF动画演示:**
|
||||
|
||||

|
||||
|
||||
### 代码:
|
||||
|
||||
```java
|
||||
public int trap02(int[] height) {
|
||||
int sum = 0;
|
||||
//最两端的列不用考虑,因为一定不会有水。所以下标从 1 到 length - 2
|
||||
for (int i = 1; i < height.length - 1; i++) {
|
||||
int max_left = 0;
|
||||
//找出左边最高
|
||||
for (int j = i - 1; j >= 0; j--) {
|
||||
if (height[j] > max_left) {
|
||||
max_left = height[j];
|
||||
}
|
||||
}
|
||||
int max_right = 0;
|
||||
//找出右边最高
|
||||
for (int j = i + 1; j < height.length; j++) {
|
||||
if (height[j] > max_right) {
|
||||
max_right = height[j];
|
||||
}
|
||||
}
|
||||
//找出两端较小的
|
||||
int min = Math.min(max_left, max_right);
|
||||
//只有较小的一段大于当前列的高度才会有水,其他情况不会有水
|
||||
if (min > height[i]) {
|
||||
sum = sum + (min - height[i]);
|
||||
}
|
||||
}
|
||||
return sum;
|
||||
}
|
||||
```
|
||||
|
||||
可以看到,上面方法的时间复杂度达到了**O(n^2)**
|
||||
|
||||
**那么有没有更好的办法来解决这个问题?**
|
||||
|
||||
下面的方法巧妙的使用了**双指针**来解决问题:
|
||||
|
||||
与上述解法的思路大致是相同的,都是单个地求出当前墙可以存储雨水的容量;这种解法也是非常的巧妙,是在浏览解题区的时候碰见的,大佬还做了视频(链接放在文末),讲解的非常清楚,我大概用自己的思路来作一文字叙述:
|
||||
|
||||
既然使用的是**twoPointers**的思路,那么我们需要分别从数组的最前面和最后面开始,这两个指针是互不影响,都是各走各的,但是如何确定当前指针走过的地方能存放多少雨水量呢?
|
||||
|
||||
这个时候,我们就需要两块挡板**leftMax**和**rightMax**,这两块挡板最开始都是挡在最外面的墙边,随着两个指针前进,**leftMax**代表的是**left**走过的路中最高的墙,**rightMax**同理。
|
||||
|
||||
**那么如何计算雨水量呢?**
|
||||
|
||||
比较左右两个挡板的高度,然后根据两个挡板各自的指针配合计算。
|
||||
|
||||
- 如果左边挡板的高度小于右边的挡板高度,那么左边指针之前的雨水量取决于**leftMax**和height[left]的大小关系,如果前者大于后者,那么容量等与前者减去后者;反之,容量为0(可以参考解法一中的图来理解)
|
||||
- 如果左边挡板的高度大于等于右边挡板的高度,与上一种情况基本相同,只不过是求的右边的雨水量。
|
||||
- 在每次移动指针之后,我们要将挡板更新到最大值。
|
||||
|
||||
**其实道理也是比较简单,用宏观的思维去看待整个问题,最起码先保证两边的墙的高度(两块挡板),然后依次去到其中各个墙之间能装多少雨水的问题上。(求每次更新最高的挡板和指针指向的墙之间可以存储的雨水量)**
|
||||
|
||||
### 代码:
|
||||
|
||||
```java
|
||||
public int trap(int[] height) {
|
||||
if (height.length == 0) return 0;
|
||||
int left = 0;
|
||||
int right = height.length-1;
|
||||
int leftMax = 0;
|
||||
int rightMax = 0;
|
||||
int result = 0;
|
||||
while (left <= right) {
|
||||
if (leftMax < rightMax) {
|
||||
result += leftMax - height[left] > 0 ?
|
||||
leftMax - height[left] : 0;
|
||||
leftMax = Math.max(leftMax, height[left]);
|
||||
left++;
|
||||
} else {
|
||||
result += rightMax - height[right] > 0 ?
|
||||
rightMax - height[right] : 0;
|
||||
rightMax = Math.max(rightMax, height[right]);
|
||||
right--;
|
||||
}
|
||||
}
|
||||
return result;
|
||||
}
|
||||
```
|
||||
|
||||
**时间复杂度:O(n) 空间复杂度:O(1)**
|
||||
|
||||
[leetcode配套视频入口](https://leetcode-cn.com/problems/trapping-rain-water/solution/javashi-pin-jiang-jie-xi-lie-trapping-rain-water-b/)
|
||||
|
||||
BIN
0058-length-Of-Last-Word/Animation/0058.gif
Normal file
|
After Width: | Height: | Size: 1.2 MiB |
76
0058-length-Of-Last-Word/Article/0058-length-Of-Last-Word.md
Normal file
@ -0,0 +1,76 @@
|
||||
## LeetCode第58号问题:最后一个单词的长度
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 个人博客:www.zhangxiaoshuai.fun
|
||||
|
||||
**本题选自leetcode第58题,easy难度,目前通过率33.0%**
|
||||
|
||||
### 题目描述:
|
||||
```txt
|
||||
给定一个仅包含大小写字母和空格' '的字符串s,返回其最后一个单词的长度。
|
||||
如果字符串从左向右滚动显示,那么最后一个单词就是最后出现的单词。
|
||||
如果不存在最后一个单词,请返回0。
|
||||
说明:一个单词是指仅由字母组成、不包含任何空格字符的最大子字符串。
|
||||
|
||||
示例:
|
||||
输入:"Hello World"
|
||||
输出:5
|
||||
```
|
||||
|
||||
### 题目分析:
|
||||
|
||||
既然需要求出最后一个单词的长度,那我们直接从**字符串的末尾**开始好了;
|
||||
这里末尾有两种情况:有空格和没有空格
|
||||
|
||||
```
|
||||
(1)有空格:我们从末尾忽略掉空格,然后找到第一个遇见的字符(遇到第一个空格或者遍历完整个字符串为止)
|
||||
(2)无空格:直接从末尾往前寻找即可(遇到第一个空格或者遍历完整个字符串为止)
|
||||
```
|
||||
|
||||
### 动画gif演示:
|
||||
|
||||

|
||||
|
||||
### 代码:
|
||||
|
||||
**The first version**
|
||||
|
||||
```java
|
||||
public int lengthOfLastWord(String s) {
|
||||
if (s.length()==0) {
|
||||
return 0;
|
||||
}
|
||||
int index = 0;
|
||||
int temp = 0;
|
||||
int p = s.length()-1;
|
||||
while ((p-index >=0) && s.charAt(p-index) == 32) index++;
|
||||
for (int i = p-index;i >= 0;i--) {
|
||||
if (s.charAt(i) != 32){
|
||||
temp++;
|
||||
continue;
|
||||
}
|
||||
break;
|
||||
}
|
||||
return temp;
|
||||
}
|
||||
```
|
||||
|
||||
**2.代码:**
|
||||
|
||||
**The second version**
|
||||
|
||||
```java
|
||||
public int lengthOfLastWord(String s) {
|
||||
int len = 0;
|
||||
for (int i = s.length() - 1; i >= 0; i--) {
|
||||
if (s.charAt(i) != ' ') {
|
||||
len++;
|
||||
} else if (len != 0) {
|
||||
return len;
|
||||
}
|
||||
}
|
||||
return len;
|
||||
}
|
||||
```
|
||||
|
||||
BIN
0088-Merge-Sorted-Array/Animation/Animation.gif
Normal file
|
After Width: | Height: | Size: 6.7 MiB |
108
0088-Merge-Sorted-Array/Article/0088-Merge-Sorted-Array.md
Normal file
@ -0,0 +1,108 @@
|
||||
# LeetCode 第 88 号问题:合并两个有序数组
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
题目来源于 LeetCode 上第 88 号问题:合并两个有序数组。题目难度为 Easy
|
||||
|
||||
### 题目描述
|
||||
|
||||
给你两个有序整数数组 *nums1* 和 *nums2*,请你将 *nums2* 合并到 *nums1* 中*,*使 *nums1* 成为一个有序数组。
|
||||
|
||||
**说明:**
|
||||
|
||||
- 初始化 *nums1* 和 *nums2* 的元素数量分别为 *m* 和 *n* 。
|
||||
- 你可以假设 *nums1* 有足够的空间(空间大小大于或等于 *m* + *n*)来保存 *nums2* 中的元素。
|
||||
|
||||
**示例:**
|
||||
|
||||
```
|
||||
输入:
|
||||
nums1 = [1,2,3,0,0,0], m = 3
|
||||
nums2 = [2,5,6], n = 3
|
||||
|
||||
输出: [1,2,2,3,5,6]
|
||||
```
|
||||
|
||||
### 题目解析
|
||||
|
||||
将这个题目放到现实中就容易多了, 不信你看看.
|
||||
|
||||
假如你是玩具店的老板, 其中两个货架依次摆放了形状相同大小不同的小汽车, 这些小汽车都按照从小到大摆放着, 现在你想把第二个货架的小汽车移到第一个货架上, 为了顾客看起来直观, 这些小汽车要摆放的有序, 你会怎么做呢?
|
||||
|
||||
**很显现, 你不会把所有小汽车放到一起, 然后在一个个排序好放到第一个货架上.**
|
||||
|
||||
你肯定会比较两个货架小汽车的大小, 把第二个货架小汽车移到第一个货架的相应位置上.
|
||||
|
||||
那么问题来了, 是从小的比较呢还是从大的比较呢?
|
||||
|
||||
**先从小的比较来看**, 现在第二个货架第一个汽车是最小的, 那么你得把第一个货架所有玩具往后挪一位, 然后才能放下这个汽车, **好像有点费力了**.
|
||||
|
||||
不想费力, 我们可以先把第一个货架的玩具移到第三个货架, 比较第二个货架和第三个货架, 把比较小的汽车放到第一个货架上. 看来还得先搬移第一个货架, **需要占用其他空间了**.
|
||||
|
||||
**如果从后面比较呢**, **也就是先比较大的汽车**, 现在第二个货架最后一个是最大的汽车, 我只需要把最大的汽车拿到第一货架的最后面就可以了, 是不是很轻松, 这样依次比较, **不费力也不用费空间**就挪到了第一个货架后面了. 和第一个货架都比较完了, 发现第二个货架还剩一个最小的汽车, 这个时候你会发现第一个货架的第一个位置是空的, 我们直接拿过去就可以啦.
|
||||
|
||||
故事讲完啦, 通过这几种方法的尝试, 你也许已经发现了:
|
||||
|
||||
> 第一种方法 对应的算法是 **' 合并后排序 '**, 时间复杂度比较大;
|
||||
>
|
||||
> 第二种方法 对应的算法是 **' 双指针 + 从前向后比较 '**
|
||||
>
|
||||
> - 往后挪动汽车时间复杂度高
|
||||
> - 移到第三个货架空间复杂度高
|
||||
>
|
||||
> 第三种方法 对应的算法是 **' 双指针 + 从后向前比较 '** , 省时又不占空间, 完美!
|
||||
|
||||
下面说下 **' 双指针 + 从后向前比较 '** 的具体思路:
|
||||
|
||||
1. 设置双指针, 分别指向有序数组的最后一位;
|
||||
|
||||
2. 从后向前
|
||||
|
||||
- 终止条件: 其中一个指针不在指向数组
|
||||
|
||||
- 比较双指针指向的值
|
||||
|
||||
- 大的或相同的值放到 *num1* 空间的尾部( 尾部从后向前依次填充 ), 对应的指针向前挪一位
|
||||
- 循环上面步骤
|
||||
|
||||
3. 遍历完成后检查
|
||||
|
||||
- 若指向 *num2* 的指针还有效, 说明 *num2* 中还有小于 *num1* 最小值的存在
|
||||
- 将这些值搬移到 *num1* 最前面
|
||||
|
||||
### 动画描述
|
||||
|
||||
<img src="../Animation/Animation.gif" alt="Animation" style="zoom:150%;" />
|
||||
|
||||
### 参考代码
|
||||
|
||||
```javascript
|
||||
/**
|
||||
* JavaScript 描述
|
||||
* 双指针 + 从后向前
|
||||
*/
|
||||
var merge = function(nums1, m, nums2, n) {
|
||||
let len = m + n;
|
||||
while(m > 0 && n > 0){
|
||||
// '>=' 相比 '>' 在某些值相同的情况下能少比较一次
|
||||
nums1[--len] = nums2[n-1] >= nums1[m-1] ? nums2[--n]: nums1[--m];
|
||||
}
|
||||
if(n > 0){
|
||||
nums1.splice(0,n,...nums2.slice(0,n));
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
- 时间复杂度: **O( m+n )**
|
||||
|
||||
- 空间复杂度: **O( 1 )**
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||

|
||||
BIN
0104-Maximum-Depth-Of-Binary-Tree/Animation/Animation1.gif
Normal file
|
After Width: | Height: | Size: 7.9 MiB |
BIN
0104-Maximum-Depth-Of-Binary-Tree/Animation/Animation2.gif
Normal file
|
After Width: | Height: | Size: 14 MiB |
@ -0,0 +1,122 @@
|
||||
# LeetCode 第 104 号问题:二叉树的最大深度
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
今天分享的题目来源于 LeetCode 上第 104 号问题:二叉树的最大深度。题目难度为 Easy 。
|
||||
|
||||
### 题目描述
|
||||
|
||||
给定一个二叉树,找出其最大深度。
|
||||
|
||||
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
|
||||
|
||||
**说明:** 叶子节点是指没有子节点的节点。
|
||||
|
||||
**示例 :**
|
||||
|
||||
给定二叉树 `[3,9,20,null,null,15,7]`,
|
||||
|
||||
```
|
||||
3
|
||||
/ \
|
||||
9 20
|
||||
/ \
|
||||
15 7
|
||||
```
|
||||
|
||||
返回它的最大深度 3 。
|
||||
|
||||
### 题目解析 - DFS
|
||||
|
||||
最直接的办法就是使用DFS ( 深度优先搜索 ) 策略计算树的高度. 具体算法流程如下:
|
||||
|
||||
- **终止条件:**当前节点为空
|
||||
- **返回值:**
|
||||
- 节点为空时,所以返回 0
|
||||
- 节点不为空时, 返回左右子树高度的最大值 + 1
|
||||
|
||||
### 动画描述
|
||||
|
||||

|
||||
|
||||
### 代码实现
|
||||
|
||||
```javascript
|
||||
/**
|
||||
* JavaScript 描述
|
||||
* DFS
|
||||
*/
|
||||
var maxDepth = function(root) {
|
||||
if (root == null) {
|
||||
return 0;
|
||||
}
|
||||
let leftHeight = maxDepth(root.left);
|
||||
let rightHeight = maxDepth(root.right);
|
||||
return Math.max(leftHeight, rightHeight) + 1;
|
||||
};
|
||||
```
|
||||
|
||||
**精简版**
|
||||
|
||||
```javascript
|
||||
var maxDepth = function(root) {
|
||||
return !root ? 0 : Math.max(maxDepth(root.left) + 1, maxDepth(root.right) + 1) ;
|
||||
};
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
- 时间复杂度:**O(n)**, 我们每个结点只访问一次,因此时间复杂度为 O(N)
|
||||
- 空间复杂度:
|
||||
- 最坏情况下,树是完全不平衡的,例如每个结点只剩下左子结点,递归将会被调用 N 次(树的高度),因此保持调用栈的存储将是 O(N)。
|
||||
- 最好情况下(树是完全平衡的),树的高度将是 log(N)。因此,在这种情况下的空间复杂度将是 O(log(N))
|
||||
|
||||
|
||||
|
||||
### 题目解析 - BFS
|
||||
|
||||
求二叉树的深度也就是求二叉树有几层了, 采用 BFS ( 广度优先搜索 ) 策略对二叉树按层遍历.
|
||||
|
||||
实现 BFS 就要用到 '先进先出' 的队列了, 具体算法流程如下:
|
||||
|
||||
- 遍历二叉树节点,依次将当前节点 和它的左右子节点入队
|
||||
- 依次出队, 出队子节点重复上一步操作
|
||||
|
||||
### 动画描述
|
||||
|
||||

|
||||
|
||||
### 代码实现
|
||||
|
||||
```javascript
|
||||
/**
|
||||
* JavaScript 描述
|
||||
* BFS
|
||||
*/
|
||||
var maxDepth = function(root) {
|
||||
let level = 0;
|
||||
if (root == null) {
|
||||
return level;
|
||||
}
|
||||
let queue = [root];
|
||||
while (queue.length) {
|
||||
let len = queue.length;
|
||||
while (len--) {
|
||||
let curNode = queue.pop();
|
||||
curNode.left && queue.unshift(curNode.left);
|
||||
curNode.right && queue.unshift(curNode.right);
|
||||
}
|
||||
level++;
|
||||
}
|
||||
return level;
|
||||
};
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
- 时间复杂度:**O(n)**
|
||||
- 空间复杂度:**O(N)**
|
||||
|
||||

|
||||
BIN
0110-Balanced-Binary-Tree/Animation/Animation1.gif
Normal file
|
After Width: | Height: | Size: 15 MiB |
BIN
0110-Balanced-Binary-Tree/Animation/Animation2.gif
Normal file
|
After Width: | Height: | Size: 16 MiB |
165
0110-Balanced-Binary-Tree/Article/0110-Balanced-Binary-Tree2.md
Normal file
@ -0,0 +1,165 @@
|
||||
# LeetCode 第 110 号问题:平衡二叉树
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
题目来源于 LeetCode 上第 110 号问题:平衡二叉树。
|
||||
|
||||
### 题目描述
|
||||
|
||||
给定一个二叉树,判断它是否是高度平衡的二叉树。
|
||||
|
||||
本题中,一棵高度平衡二叉树定义为:
|
||||
|
||||
> 一个二叉树*每个节点* 的左右两个子树的高度差的绝对值不超过1。
|
||||
|
||||
**示例 1:**
|
||||
|
||||
```
|
||||
3
|
||||
/ \
|
||||
9 20
|
||||
/ \
|
||||
15 7
|
||||
```
|
||||
|
||||
返回 `true` 。
|
||||
|
||||
**示例 2:**
|
||||
|
||||
给定二叉树 `[1,2,2,3,3,null,null,4,4]`
|
||||
|
||||
```
|
||||
1
|
||||
/ \
|
||||
2 2
|
||||
/ \
|
||||
3 3
|
||||
/ \
|
||||
4 4
|
||||
```
|
||||
|
||||
返回 `false` 。
|
||||
|
||||
### 题目解析 - 自顶向下
|
||||
|
||||
这道题可以算是递归的充分使用了, 每一个子树都是子问题.
|
||||
|
||||
根据题意, 直观的想法就是计算当前节点左右子树的高度差了, 具体算法流程如下:
|
||||
|
||||
*定义* 方法 `depth(root)` 计算 root 最大高度
|
||||
|
||||
- **终止条件:** 当 `root` 为空,即越过叶子节点,则返回高度 0
|
||||
- **返回值:** Max(左子树高度, 右子树高度 ) + 1
|
||||
|
||||
*定义* 方法 `isBalanced(root)` 判断树 `root` 是否平衡
|
||||
|
||||
- **特例处理:** 若树根节点 `root` 为空,则直接返回 true
|
||||
- **返回值:** 所有子树都需要满足平衡树性质,因此以下三者使用与 逻辑与 连接
|
||||
- `abs(depth(root.left) - depth(root.right)) < 2` :判断 **当前子树** 是否是平衡树
|
||||
- `isBalanced(root.left)` : 先序遍历递归,判断 **当前子树的左子树** 是否是平衡树;
|
||||
- `isBalanced(root.right)` : 先序遍历递归,判断 **当前子树的右子树** 是否是平衡树;
|
||||
|
||||
> 通过流程能发现, 暴力法虽然容易想到, 但是会产生大量冗余计算, 因此时间复杂度也就会高;
|
||||
>
|
||||
> 想避免这种情况, 移步向下看 自底向上 方法
|
||||
|
||||
### 动画描述
|
||||
|
||||
<img src="../Animation/Animation1.gif" alt="Animation1" style="zoom:150%;" />
|
||||
|
||||
### 参考代码
|
||||
|
||||
```javascript
|
||||
/**
|
||||
* JavaScript 描述
|
||||
* 自顶向下递归
|
||||
*/
|
||||
function depth(root) {
|
||||
if (root == null) {
|
||||
return 0;
|
||||
}
|
||||
return Math.max(depth(root.left), depth(root.right)) + 1;
|
||||
};
|
||||
var isBalanced = function(root) {
|
||||
if (root == null) {
|
||||
return true;
|
||||
}
|
||||
return Math.abs(depth(root.left) - depth(root.right)) < 2 &&
|
||||
isBalanced(root.left) &&
|
||||
isBalanced(root.right);
|
||||
};
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
- 时间复杂度: **O(Nlog_2 N)**
|
||||
|
||||
最差情况下, isBalanced(root) 遍历树所有节点,占用 O(N)O(N) ;判断每个节点的最大高度 depth(root) 需要遍历 各子树的所有节点 ,子树的节点数的复杂度为 O(log_2 N)
|
||||
|
||||
- 空间复杂度: **O(N)**
|
||||
|
||||
最差情况下(树退化为链表时),系统递归需要使用 O(N) 的栈空间
|
||||
|
||||
### 题目解析 - 自底向上
|
||||
|
||||
**自顶向下** 计算 `depth` 存在大量冗余, 每次调用 `depth` 时,要同时计算其子树高度。
|
||||
|
||||
**自底向上** 计算每个子树的高度只会计算一次。先递归计算当前节点的子节点高度,然后再通过子节点高度判断当前节点是否平衡,从而消除冗余。
|
||||
|
||||
**自底向上** 与 **自顶向下** 的逻辑相反,首先判断子树是否平衡,然后比较子树高度判断父节点是否平衡。算法如下:
|
||||
|
||||
*定义* 方法 `recur(root):` : 判断子树是否平衡 | 返回当前节点高度
|
||||
|
||||
- **递归终止条件:**
|
||||
- 当越过叶子节点时, 返回高度 0
|
||||
- 当左(右)子树高度 `left== -1` 时,代表此子树的 **左(右)子树** 不是平衡树, 因此直接返回 `-1`
|
||||
- **递归返回值:**
|
||||
- 当节点 `root` 左 / 右子树的高度差 < 2:返回以节点 root 为根节点的子树的最大高度Max( left, right ) + 1
|
||||
- 当节点 `root` 左 / 右子树的高度差 >= 2 :则返回 `-1` , 代表 **此子树不是平衡树**
|
||||
|
||||
*定义* 方法 `isBalanced(root)` : 判断当前树是否平衡
|
||||
|
||||
- **返回值:** 若 `recur(root) != 1` , 则说明此树平衡, 返回 `true` , 否则返回 `false`
|
||||
|
||||
### 动画描述
|
||||
|
||||
<img src="../Animation/Animation2.gif" alt="Animation2" style="zoom:150%;" />
|
||||
|
||||
### 参考代码
|
||||
|
||||
```javascript
|
||||
/**
|
||||
* JavaScript 描述
|
||||
* 自底向上递归
|
||||
*/
|
||||
function recur(root) {
|
||||
if (root == null) {
|
||||
return 0;
|
||||
}
|
||||
let leftHeight = recur(root.left);
|
||||
if (leftHeight == -1) {
|
||||
return -1;
|
||||
}
|
||||
let rightHeight = recur(root.right);
|
||||
if (rightHeight == -1) {
|
||||
return -1;
|
||||
}
|
||||
return Math.abs(leftHeight - rightHeight) < 2 ?
|
||||
Math.max(leftHeight,rightHeight) + 1 : -1;
|
||||
};
|
||||
var isBalanced = function(root) {
|
||||
return recur(root) != -1;
|
||||
};
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
- 时间复杂度 **O(N)**: N为树的节点数;最差情况下,需要递归遍历树的所有节点。
|
||||
- 空间复杂度 **O(N)**: 最差情况下(树退化为链表时),系统递归需要使用 O(N) 的栈空间。
|
||||
|
||||
|
||||
|
||||
|
||||

|
||||
BIN
0118-Generate/Animation/resource.gif
Normal file
|
After Width: | Height: | Size: 28 KiB |
71
0118-Generate/Article/0118-Generate.md
Normal file
@ -0,0 +1,71 @@
|
||||
## LeetCode第118号问题:杨辉三角
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 个人博客:www.zhangxiaoshuai.fun
|
||||
|
||||
**本题选自leetcode第118题,easy级别,目前通过率66.4%**
|
||||
### 题目描述:
|
||||
```
|
||||
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
|
||||
示例:
|
||||
|
||||
输入: 5
|
||||
输出:
|
||||
[
|
||||
[1],
|
||||
[1,1],
|
||||
[1,2,1],
|
||||
[1,3,3,1],
|
||||
[1,4,6,4,1]
|
||||
]
|
||||
```
|
||||
|
||||
### 题目分析:
|
||||
初中时候学习的杨辉三角想不到又在这里出现了,题意很容易理解,每一行中的第一个数字和最后一个数字都是1,中间的数字都是通过上面相邻的两个数字相加得到。题目给我们一个杨辉三角的非负行数,然后我们生成对应的杨辉三角(集合)。
|
||||
既然返回的是一个List<List<Integer>>,那么我们用一个大集合来放置每一行的数,每一行的数我们分别用一个小集合来存放,最后将每一个小集合添加进大集合中。
|
||||
|
||||
### gif动画演示:
|
||||
|
||||
官方中已经有做的非常好的gif图解,这里直接展示:
|
||||
|
||||

|
||||
|
||||
### 代码:
|
||||
|
||||
```java
|
||||
public List<List<Integer>> generate(int numRows) {
|
||||
List<List<Integer>> triangle = new ArrayList<List<Integer>>();
|
||||
//给定的numRows为0时直接返回空集合即可
|
||||
if (numRows == 0) {
|
||||
return triangle;
|
||||
}
|
||||
|
||||
//因为杨辉三角的第一行总是1,所以先新建一个list,并将1加入该list中
|
||||
triangle.add(new ArrayList<>());
|
||||
triangle.get(0).add(1);
|
||||
|
||||
//从第二行开始,新建表示当前行的list,拿到当前行的前一行的list
|
||||
for (int rowNum = 1; rowNum < numRows; rowNum++) {
|
||||
List<Integer> row = new ArrayList<>();
|
||||
List<Integer> prevRow = triangle.get(rowNum-1);
|
||||
|
||||
//一行中的第一个元素
|
||||
row.add(1);
|
||||
|
||||
//针对每一行,都是上一行的相邻的两个元素相加得到两个1中间的数
|
||||
for (int j = 1; j < rowNum; j++) {
|
||||
row.add(prevRow.get(j-1) + prevRow.get(j));
|
||||
}
|
||||
|
||||
//一行中的最后一个元素
|
||||
row.add(1);
|
||||
|
||||
//最后将“整行添加到大集合中”
|
||||
triangle.add(row);
|
||||
}
|
||||
return triangle;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
BIN
0133-Clone-Graph/Animation/133.gif
Normal file
|
After Width: | Height: | Size: 11 MiB |
BIN
0133-Clone-Graph/Animation/133.m4v
Normal file
65
0133-Clone-Graph/Article/0133-Clone-Graph.md
Normal file
@ -0,0 +1,65 @@
|
||||
# LeetCode 第 133 号问题:克隆图
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
题目来源于 LeetCode 上第 133 号问题:克隆图。题目难度为 Medium,目前通过率为 54.8% 。
|
||||
|
||||
### 题目描述
|
||||
|
||||
给你无向连通图中一个节点的引用,请你返回该图的深拷贝(克隆)。图中的每个节点都包含它的值 val(int)和其邻居的列表(list[Node])。
|
||||
|
||||
|
||||
**示例 1:**
|
||||
|
||||
```
|
||||
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
|
||||
输出:[[2,4],[1,3],[2,4],[1,3]]
|
||||
解释:
|
||||
图中有 4 个节点。
|
||||
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
|
||||
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
|
||||
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
|
||||
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
|
||||
```
|
||||
|
||||
**示例 2:**
|
||||
|
||||
```
|
||||
输入:adjList = [[]]
|
||||
输出:[[]]
|
||||
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。
|
||||
```
|
||||
|
||||
**示例 3:**
|
||||
|
||||
```
|
||||
输入:adjList = [[2],[1]]
|
||||
输出:[[2],[1]]
|
||||
```
|
||||
|
||||
### 题目解析
|
||||
|
||||
给你一个图,让你完整地拷贝一份。这道题目不难,但是在实际的工作项目中却时常遇到。这道题目有很多种解法,但是建议站在实际工作的角度去思考。
|
||||
|
||||
图是由一个个节点组成的,完整地拷贝一份图,那么就意味着我们要对每个节点进行拷贝,而且节点与节点的关系也要拷贝过来。做到这一点也不难,我们只需要遍历一遍图就可以了,这里的关键点在于题目强调是 **无向图**,也就是说我们可以从图上的任意点出发到达图上的所有节点。那么问题从而就转换到了如何遍历图,我们可以使用广度优先搜索,也可以使用深度优先搜索,从工作的角度出发,比较推荐广度优先搜索,因为理解容易,实现简单,而且不涉及栈溢出的问题,处理大规模数据比较安全。
|
||||
|
||||
<br>
|
||||
|
||||
### 动画演示
|
||||
|
||||

|
||||
|
||||
<br>
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
一般使用广度优先搜索遍历图,时间复杂度是 `O(n + m)`,其中这里的 n 表示的是图上的节点数,m 表示的图上的边的数量。从广度优先搜索的 **由点及面** 的性质,你不难理解这个结果。极端情况下,当这张图是一张全联通的图,时间复杂度就会是 `O(n^2)`,解释起来也很容易,因为你每访问完一个节点,下面都会去访问相邻的节点,一个节点和所有的节点相连,那么在一个节点上花费的时间就是 n,在 n 节点上花费的时间就是 n^2。因为我们使用了队列存放接下来需要遍历的节点,空间复杂度就是 `O(n)`。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||

|
||||
BIN
0142-Linked-List-Cycle-ii/Animation/Animation.gif
Normal file
|
After Width: | Height: | Size: 5.1 MiB |
176
0142-Linked-List-Cycle-ii/Article/0142-Linked-List-Cycle-ii.md
Normal file
@ -0,0 +1,176 @@
|
||||
# LeetCode 第 142 号问题:环形链表 II
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
今天分享的题目来源于 LeetCode 上第 142 号问题:环形链表II。题目难度为 Medium 。
|
||||
|
||||
### 题目描述
|
||||
|
||||
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 `null`。
|
||||
|
||||
为了表示给定链表中的环,我们使用整数 `pos` 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 `pos` 是 `-1`,则在该链表中没有环。
|
||||
|
||||
**示例 1:**
|
||||
|
||||
```
|
||||
输入:head = [3,2,0,-4], pos = 1
|
||||
输出:tail connects to node index 1
|
||||
解释:链表中有一个环,其尾部连接到第二个节点。
|
||||
```
|
||||
|
||||
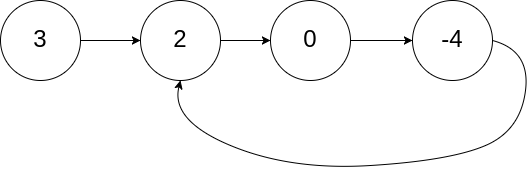
|
||||
|
||||
**示例 2:**
|
||||
|
||||
```
|
||||
输入:head = [1,2], pos = 0
|
||||
输出:tail connects to node index 0
|
||||
解释:链表中有一个环,其尾部连接到第一个节点。
|
||||
```
|
||||
|
||||
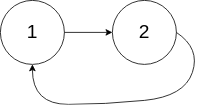
|
||||
|
||||
**示例 3:**
|
||||
|
||||
```
|
||||
输入:head = [1], pos = -1
|
||||
输出:no cycle
|
||||
解释:链表中没有环。
|
||||
```
|
||||
|
||||

|
||||
|
||||
**进阶:**
|
||||
|
||||
你是否可以不用额外空间解决此题?
|
||||
|
||||
### 题目解析 - 哈希表
|
||||
|
||||
普通解法就是利用哈希表保存访问过的节点, 同时遍历过程中检查哈希表中是否已存在相同的节点
|
||||
|
||||
### 代码实现
|
||||
|
||||
```javascript
|
||||
/**
|
||||
* JavaScript 描述
|
||||
* 哈希表方法
|
||||
*/
|
||||
var detectCycle = function(head) {
|
||||
let res = [ ];
|
||||
while (head !== null) {
|
||||
if (res.includes(head)) {
|
||||
return head;
|
||||
}
|
||||
res.push(head);
|
||||
head = head.next;
|
||||
}
|
||||
return null;
|
||||
};
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
- 时间复杂度:**O(n)**
|
||||
- 空间复杂度:**O(n)**
|
||||
|
||||
### 题目解析 - Floyd 算法
|
||||
|
||||
Floyd算法 可以达到常量空间解决此问题.
|
||||
|
||||
我在维基百科找到了这个算法描述, 在此引用一下.
|
||||
|
||||
**Floyd判圈算法**(**Floyd Cycle Detection Algorithm**),又称 **龟兔赛跑算法**(**Tortoise and Hare Algorithm**),是一个可以在[有限状态机](https://zh.wikipedia.org/wiki/有限状态机)、[迭代函数](https://zh.wikipedia.org/wiki/迭代函数)或者[链表](https://zh.wikipedia.org/wiki/链表)上判断是否存在[环](https://zh.wikipedia.org/wiki/環_(圖論)),求出该环的起点与长度的算法。
|
||||
|
||||
如果有限状态机、迭代函数或者链表存在环,那么一定存在一个起点可以到达某个环的某处 ( 这个起点也可以在某个环上 )。
|
||||
|
||||
初始状态下,假设已知某个起点节点为节点 *S*。现设两个指针 `t` 和 `h` ,将它们均指向 *S*。
|
||||
|
||||
接着,同时让 `t` 和 `h` 往前推进,但是二者的速度不同:`t` 每前进 `1` 步, `h` 前进 `2` 步。只要二者都可以前进而且没有相遇,就如此保持二者的推进。当 `h` 无法前进,即到达某个没有后继的节点时,就可以确定从 *S* 出发不会遇到环。反之当 `t` 与 `h` 再次相遇时,就可以确定从 S 出发一定会进入某个环,设其为环 *C*。
|
||||
|
||||
如果确定了存在某个环,就可以求此环的起点与长度。
|
||||
|
||||
上述算法刚判断出存在环 *C* 时,显然 t 和 `h` 位于同一节点,设其为节点 *M*。显然,仅需令 `h` 不动,而t不断推进,最终又会返回节点 *M*,统计这一次t推进的步数,显然这就是环 *C* 的长度。
|
||||
|
||||
为了求出环 *C* 的起点,只要令h仍均位于节点 *M* ,而令t返回起点节点 *S* ,此时h与t之间距为环 *C* 长度的整数倍。随后,同时让 `t` 和 `h` 往前推进,且保持二者的速度相同:`t` 每前进 `1` 步,`h` 前进 `1` 步。持续该过程直至 `t` 与 `h` 再一次相遇,设此次相遇时位于同一节点 *P*,则节点 *P* 即为从节点 *S* 出发所到达的环 *C* 的第一个节点,即环 *C* 的一个起点。
|
||||
|
||||
**看完之后是不是很多疑点, 觉得为什么会这样呢?**
|
||||
|
||||
下面用数学简单证明一下
|
||||
|
||||
假设 链表的节点数为 `num`, 从 head 到链表环入口节点数为 `m` (不包含入口节点), 环的节点数为 `n`, 链表环入口设点为 *P*
|
||||
|
||||
由此可得 `num = m + n`
|
||||
|
||||
假设 慢指针 `Tortoise` (乌龟) 每次走 `1` 个节点, 走了 `x` 步
|
||||
|
||||
假设 快指针 `Hare` (兔子) 每次走 `2` 个节点, 走了 `f` 步
|
||||
|
||||
那么 `f = 2x`
|
||||
|
||||
当第一次相遇时, 必然是在环内, 设其点为 *M*, 兔子第一次到达 *M* 点后至少又在环内饶了一圈后追上乌龟,
|
||||
|
||||
假设绕了 `k` 圈, 那么可以得到
|
||||
|
||||
`f = x + kn`
|
||||
|
||||
兔子到达 *P* 点的步数为
|
||||
|
||||
`f = m + kn`
|
||||
|
||||
由 `f = 2x` 和 `f = x + kn` 两个等式可以得到 `x = kn`
|
||||
|
||||
由 `f = m + kn` 和 `x = kn` 可知, 乌龟到达 *P* 点还需要走 `m` 步
|
||||
|
||||
而 `m` 的长度正是从 head 到链表环入口节点数的长度, 这是未知的,
|
||||
|
||||
那么让兔子从 head 以乌龟的速度走, 乌龟在 *M* 点走, 当兔子和乌龟相遇时即走了 `m` 步, 也就到达了 *P* 节点.
|
||||
|
||||
### 动画描述
|
||||
|
||||

|
||||
|
||||
### 代码实现
|
||||
|
||||
```java
|
||||
/**
|
||||
* JavaScript 描述
|
||||
* Floyd判圈算法
|
||||
*/
|
||||
var detectCycle = function(head) {
|
||||
if (head == null) {
|
||||
return head;
|
||||
}
|
||||
// 设置快慢指针
|
||||
let tortoise = head,
|
||||
hare = head;
|
||||
// 检查链表是否有环
|
||||
while (true) {
|
||||
if (hare == null || hare.next == null) {
|
||||
return null;
|
||||
}
|
||||
hare = hare.next.next;
|
||||
tortoise = tortoise.next;
|
||||
if (hare == tortoise) {
|
||||
break;
|
||||
}
|
||||
}
|
||||
// 兔子和乌龟第二次相遇找到环入口
|
||||
hare = head;
|
||||
while (hare != tortoise) {
|
||||
hare = hare.next;
|
||||
tortoise = tortoise.next;
|
||||
}
|
||||
return hare;
|
||||
};
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
- 时间复杂度:**O(n)**
|
||||
- 有环情况下, 第一次和第二次相遇, 乌龟步数都小于链表节点数, 因此与链表节点数成线性关系;
|
||||
- 无环情况下, 兔子大约需要 n/2 步数到达最后, 因此也与链表节点数成线性关系.
|
||||
- 空间复杂度:**O(1)** , 双指针使用常数大小的额外空间
|
||||
|
||||

|
||||
BIN
0234-isPalindrome/Animation/solved01.gif
Normal file
|
After Width: | Height: | Size: 2.9 MiB |
BIN
0234-isPalindrome/Animation/solved02.gif
Normal file
|
After Width: | Height: | Size: 3.1 MiB |
111
0234-isPalindrome/Article/0234-isPalindrome.md
Normal file
@ -0,0 +1,111 @@
|
||||
## LeetCode第234号问题:回文链表
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 个人博客:www.zhangxiaoshuai.fun
|
||||
|
||||
**本题选择leetcode第234题,easy难度,目前通过率41.5%**
|
||||
|
||||
```txt
|
||||
题目描述:
|
||||
请判断一个链表是否为回文链表。
|
||||
示例 1:
|
||||
输入: 1->2
|
||||
输出: false
|
||||
|
||||
示例 2:
|
||||
输入: 1->2->2->1
|
||||
输出: true
|
||||
```
|
||||
|
||||
***这道题还有进阶版本,我们先实现这个普通版本再看。***
|
||||
|
||||
### 题目分析:
|
||||
|
||||
```
|
||||
首先,我们先遍历一遍链表,将链表中的每个值存入数组当中,然后我们判断数组中的元素是否满足回文数条件即可。
|
||||
这里因为我们不知道链表的长度,我们先使用动态数组将值存起来,然后再存到固定大小的数组中。
|
||||
```
|
||||
|
||||
### 解法一gif动画演示:
|
||||
|
||||

|
||||
|
||||
### 代码:
|
||||
|
||||
```java
|
||||
public boolean isPalindrome(ListNode head) {
|
||||
List<Integer> list = new ArrayList<>();
|
||||
while (head != null) {
|
||||
list.add(head.val);
|
||||
head = head.next;
|
||||
}
|
||||
int[] arr = new int[list.toArray().length];
|
||||
int temp = 0;
|
||||
for (int a : list) {
|
||||
arr[temp++] = a;
|
||||
}
|
||||
temp = 0;
|
||||
for (int i = 0;i < arr.length/2;i++) {
|
||||
if (arr[i] == arr[arr.length-i-1]) {
|
||||
temp++;
|
||||
}
|
||||
}
|
||||
if(temp == arr.length/2) return true;
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
**时间复杂度:O(n) 空间复杂度:O(n)**
|
||||
|
||||
### 进阶:
|
||||
|
||||
**你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?**
|
||||
|
||||
**思路分析:**我们先找到链表的中间结点,然后将中间结点后面的链表进行反转,反转之后再和前半部分链表进行比较,如果相同则表示该链表属于回文链表,返回true;否则,否则返回false
|
||||
|
||||
### 解法二gif动画演示:
|
||||
|
||||

|
||||
|
||||
### 代码:
|
||||
|
||||
```java
|
||||
public boolean isPalindrome(ListNode head) {
|
||||
if(head == null || head.next == null) return true;
|
||||
ListNode p = new ListNode(-1);
|
||||
ListNode low = p;
|
||||
ListNode fast = p;
|
||||
p.next = head;
|
||||
//使用快慢指针来确定中间结点
|
||||
while(fast != null && fast.next != null){
|
||||
low = low.next;
|
||||
fast = fast.next.next;
|
||||
}
|
||||
ListNode cur = low.next;
|
||||
ListNode pre = null;
|
||||
low.next = null;
|
||||
low = p.next;
|
||||
|
||||
//反转后半部分链表
|
||||
while(cur != null){
|
||||
ListNode tmp = cur.next;
|
||||
cur.next = pre;
|
||||
pre = cur;
|
||||
cur = tmp;
|
||||
}
|
||||
//将前半部分链表和后半部分进行比较
|
||||
while(pre != null){
|
||||
if(low.val != pre.val){
|
||||
return false;
|
||||
}
|
||||
low = low.next;
|
||||
pre = pre.next;
|
||||
}
|
||||
return true;
|
||||
}
|
||||
```
|
||||
|
||||
**时间复杂度:O(n) 空间复杂度:O(1)**
|
||||
|
||||
**没错,可以看到上面的代码是完全能可以通过的,虽然我们完成了题目,但是我们改变了链表的结构,也就是说它现在不是它了;出题人应该是不希望我们破坏链表的,所以在我们完成判断之后,需要将链表恢复原样,也就是将后半部分链表反转之后接到前半部分链表的末尾。**
|
||||
@ -2,7 +2,7 @@
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步个人博客:https://www.zhangxiaoshuai.fun
|
||||
> 同步个人博客:www.zhangxiaoshuai.fun
|
||||
|
||||
|
||||
```txt
|
||||
|
||||
BIN
0461-hamming-distance/Animation/Animation.mp4
Normal file
172
0461-hamming-distance/Article/0461-hamming-distance.md
Normal file
@ -0,0 +1,172 @@
|
||||
### 题目描述
|
||||
|
||||
两个整数之间的[汉明距离](https://baike.baidu.com/item/汉明距离)指的是这两个数字对应二进制位不同的位置的数目。
|
||||
|
||||
给出两个整数 `x` 和 `y`,计算它们之间的汉明距离。
|
||||
|
||||
示例 :
|
||||
|
||||
```
|
||||
输入: x = 1, y = 4
|
||||
|
||||
输出: 2
|
||||
|
||||
解释:
|
||||
1 (0 0 0 1)
|
||||
4 (0 1 0 0)
|
||||
↑ ↑
|
||||
```
|
||||
|
||||
### 题目解析
|
||||
|
||||
首先通过 异或 操作找出两个数字对应位不同的位置,然后统计这些位置的个数。
|
||||
|
||||
统计解法借鉴Java中Integer.bitCount()方法源码来进行讲解,通过固定步数得到异或后1的个数。
|
||||
|
||||
第一步:将奇数位与偶数位相加,可以得出每两位1的个数,并将个数记录在这两位空间中
|
||||
|
||||
> i = i - (( i >>> 1 ) & 0x55555555 )
|
||||
>
|
||||
> ```
|
||||
> 0x55555555 => 01 01 01 01 ... 01 01
|
||||
> i & 0x55555555 取出奇数位的1
|
||||
> (i >>> 1) & 0x55555555 取出偶数位的1
|
||||
> 比如,两位的情况下总共就四种情况:00 11 01 10
|
||||
> 假设 i = 00 11 01 10
|
||||
> i & 0x55555555 = 00 11 01 10
|
||||
> 01 01 01 01
|
||||
> -----------
|
||||
> 00 01 01 00
|
||||
> (i >>> 1) & 0x55555555 = 00 01 10 11
|
||||
> 01 01 01 01
|
||||
> -----------
|
||||
> 00 01 00 01
|
||||
> 将奇数位1的个数与偶数位的1求和:
|
||||
> 00 01 01 00
|
||||
> 00 01 00 01
|
||||
> -----------
|
||||
> 00 10 01 01
|
||||
> 结合原数字可以看出,00(00:没有1) 11(10:两个1) 01(01:1个1) 10(01:1个1)
|
||||
>
|
||||
> 每两位在通过加法统计时,总共如下四种情况[i & 01 + (i>>>1) & 01]:
|
||||
> 11: 01 + 01 = 10 = 2, 10: 00 + 01 = 01 = 1, 01: 01 + 00 = 01 = 1, 00: 00 + 00 = 00 = 0
|
||||
> 每两位在通过减法统计时,总共如下四种情况[i - (i>>>1) & 01]:
|
||||
> 11: 11 - 01 = 10 = 2, 10: 10 - 01 = 01 = 1, 01: 01 - 00 = 01 = 1, 00: 00 + 00 = 00 = 0
|
||||
> 可以发现结果是一样的,但是少了一次位运算!
|
||||
>
|
||||
> 在将每两位1的个数统计完之后,就可以开始两位两位、四位四位...相加求出1的总数
|
||||
> ```
|
||||
|
||||
第二步:通过相邻两位1的个数相加,求出每四位包含1的个数,并将结果存储在所在的四位中
|
||||
|
||||
> i = ( i & 0x33333333 ) + (( i >>> 2 ) & 0x33333333 )
|
||||
>
|
||||
> ```
|
||||
> 0x55555555 => 0011 0011 0011 ... 0011 0011
|
||||
> 继续上一步的结果向下进行:00 10 01 01
|
||||
> i & 0x33333333 = 0010 0101
|
||||
> 0011 0011
|
||||
> ---------
|
||||
> 0010 0001
|
||||
> (i >>> 2) & 0x33333333 = 0000 1001
|
||||
> 0011 0011
|
||||
> ---------
|
||||
> 0000 0001
|
||||
>
|
||||
> 就和得出每四位所包含1的个数
|
||||
> 0010 0001
|
||||
> 0000 0001
|
||||
> ---------
|
||||
> 0010 0010
|
||||
> 结合原数字可以看出,0011(0010:有两个1) 0110(0010:有两个1)
|
||||
> ```
|
||||
|
||||
第三步:通过相邻四位1的个数相加,求出每八位包含1的个数,并将结果存储在所在的八位中
|
||||
|
||||
>i = ( i + ( i >>> 4 )) & 0x0f0f0f0f;
|
||||
>
|
||||
>```
|
||||
>0x0f0f0f0f => 00001111 ... 00001111
|
||||
>继续上一步的结果向下进行:0010 0010
|
||||
>i & 0x0f0f0f0f = 00100010
|
||||
> 00001111
|
||||
> --------
|
||||
> 00000010
|
||||
>(i >>> 4) & 0x0f0f0f0f = 00000010
|
||||
> 00001111
|
||||
> --------
|
||||
> 00000010
|
||||
>就和得出每八位所包含1的个数
|
||||
>00000010
|
||||
>00000010
|
||||
>--------
|
||||
>00000100
|
||||
>结合原数字可以看出,00110110(00000100:有四个1)
|
||||
>
|
||||
>源码中直接先将相邻四位进行相加,然后做了一次无用位清除
|
||||
>```
|
||||
|
||||
第四步:通过相邻八位1的个数相加,求出每十六位包含1的个数,并将结果存储在所在的十六位中
|
||||
|
||||
> i = i + ( i >>> 8 );
|
||||
>
|
||||
> ```
|
||||
> 可以理解为( i & 0x0f0f0f0f ) + (( i >>> 8 ) & 0x0f0f0f0f );
|
||||
>
|
||||
> 0x0f0f0f0f => 00000000111111110000000011111111
|
||||
> ```
|
||||
|
||||
第五步:通过将int类型前十六位1的个数与后16位1的个数相加,求出int中所有1的个数
|
||||
|
||||
> i = i + ( i >>> 16 );
|
||||
>
|
||||
> ```
|
||||
> 可以理解为( i & 0x0000ffff ) + (( i >>> 8 ) & 0x0000ffff );
|
||||
>
|
||||
> 0x0000ffff => 00000000000000001111111111111111
|
||||
> ```
|
||||
|
||||
第六步:去除无用的位
|
||||
|
||||
> return i & 0x3f;
|
||||
>
|
||||
> ```
|
||||
> int类型32位,即最多0x100000个1,除此之外左边的位都是无用的。
|
||||
> 0x3f => 00111111
|
||||
> ```
|
||||
|
||||
### 动画理解
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
|
||||
### 参考代码
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int hammingDistance(int x, int y) {
|
||||
return Integer.bitCount(x ^ y);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
bitCount源码:
|
||||
|
||||
```java
|
||||
public static int bitCount(int i) {
|
||||
i = i - ((i >>> 1) & 0x55555555);
|
||||
i = (i & 0x33333333) + ((i >>> 2) & 0x33333333);
|
||||
i = (i + (i >>> 4)) & 0x0f0f0f0f;
|
||||
i = i + (i >>> 8);
|
||||
i = i + (i >>> 16);
|
||||
return i & 0x3f;
|
||||
}
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
时间复杂度:O(1)
|
||||
|
||||
空间复杂度:O(1)
|
||||
BIN
0477-total-hamming-distance/Animation/Animation.mp4
Executable file
102
0477-total-hamming-distance/Article/0477-total-hamming-distance.md
Executable file
@ -0,0 +1,102 @@
|
||||
### 题目描述
|
||||
|
||||
两个整数的 [汉明距离](https://baike.baidu.com/item/汉明距离/475174?fr=aladdin) 指的是这两个数字的二进制数对应位不同的数量。
|
||||
|
||||
计算一个数组中,任意两个数之间汉明距离的总和。
|
||||
|
||||
示例 :
|
||||
|
||||
```
|
||||
输入: 4, 14, 2
|
||||
|
||||
输出: 6
|
||||
|
||||
解释: 在二进制表示中,4表示为0100,14表示为1110,2表示为0010。(这样表示是为了体现后四位之间关系)
|
||||
所以答案为:
|
||||
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.
|
||||
```
|
||||
|
||||
**注意:**
|
||||
|
||||
1. 数组中元素的范围为从 `0`到 `10^9`。
|
||||
2. 数组的长度不超过 `10^4`。
|
||||
|
||||
### 题目解析
|
||||
|
||||
已示例为例,两两暴力计算的时间复杂度为o(n^2),实现上肯定是没有问题,但是当数据量大的时候性能堪忧。
|
||||
|
||||
我们先将数组与结果的数字二进制写出来
|
||||
|
||||
```
|
||||
4 0 1 0 0
|
||||
14 1 1 1 0
|
||||
2 0 0 1 0
|
||||
HammingDistance(4, 14) = 1 0 1 0
|
||||
HammingDistance(4, 2) = 0 1 1 0
|
||||
HammingDistance(14, 2) = 1 1 0 0
|
||||
```
|
||||
|
||||
结合结果,从左往右按列观察这三个数字的二进制与运算结果的二进制可以发现一种关系:
|
||||
|
||||
数字个数 Count = 3
|
||||
|
||||
第一列: 0 1 0 ==> 1 * (3 -1) = 2 = 1 0 1
|
||||
|
||||
> 本列只有1个1,说明在所有数字的第一位中,有(Count - 1)个数字的第一位与 **本数字** 不同,也就是求距离的时候结果为1, 即这一位产生1的个数为1 * (3 -1)
|
||||
|
||||
第二列: 1 1 0 ==> 2 * (3 -2) = 2 = 0 1 1
|
||||
|
||||
> 本列有2个1,说明在所有数字的第二位中,有(Count - 2)个数字的第二位与这 **两个数字** 不同,即这一位产生1的个数为(Count - 2)+ (Count - 2)= 2 *(3 - 2)
|
||||
|
||||
第三列同第二列
|
||||
|
||||
第四列: 0 0 0 ==> 0 * (3 -0) = 0 = 0 0 0
|
||||
|
||||
> 本列所有数字相同,求距离时也就不会产生1, 结果为0
|
||||
>
|
||||
> 如果是 1 1 1也一样,3 * (3 - 3), 结果依旧为0
|
||||
|
||||
总结 :每一列求距离产生1的个数 = 本列 1 的个数 * (数字个数 – 本列1的个数)= 本列 1 的个数 * 本列 0 的个数
|
||||
|
||||
### 动画理解
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 参考代码
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int totalHammingDistance(int[] nums) {
|
||||
int len=nums.length;
|
||||
int[] bitCount = new int[32];
|
||||
if(len <= 1){
|
||||
return 0;
|
||||
}
|
||||
for(int numIndex = 0; numIndex < len; numIndex++){
|
||||
for(int bitIndex = 0; bitIndex < 32; bitIndex++){
|
||||
bitCount[bitIndex] += nums[numIndex] & 1;
|
||||
nums[numIndex] = nums[numIndex] >> 1;
|
||||
if(nums[numIndex] == 0){
|
||||
break;
|
||||
}
|
||||
}
|
||||
}
|
||||
int oneCount = 0;
|
||||
for(int bitIndex = 0; bitIndex < 32; bitIndex++){
|
||||
oneCount += bitCount[bitIndex] * (len - bitCount[bitIndex]);
|
||||
}
|
||||
return oneCount;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
时间复杂度:时间复杂度:O(N log C) 其中 C是常数,表示数组中数可能的最大值。
|
||||
|
||||
空间复杂度:O(log C)
|
||||
@ -1,6 +1,8 @@
|
||||
## LeetCode第994号问题:腐烂的橘子
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步个人博客:https://www.zhangxiaoshuai.fun
|
||||
> 同步个人博客:www.zhangxiaoshuai.fun
|
||||
|
||||
本题在leetcode中题目序号994,属于medium级别,目前通过率为50.7%
|
||||
|
||||
|
||||
BIN
1137-Tribonacci/Animation/1137-Tribonacci.gif
Normal file
|
After Width: | Height: | Size: 1.5 MiB |
BIN
1137-Tribonacci/Animation/1137-Tribonacci.mp4
Normal file
89
1137-Tribonacci/Article/1137-Tribonacci.md
Normal file
@ -0,0 +1,89 @@
|
||||
## LeetCode第1137号问题:第N个泰波那契数
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 个人博客:www.zhangxiaoshuai.fun
|
||||
|
||||
**本题选自leetcode中第1137题,easy级别,目前通过率52.4%**
|
||||
|
||||
### 题目描述:
|
||||
|
||||
```txt
|
||||
泰波那契序列 Tn 定义如下:
|
||||
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
|
||||
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。
|
||||
|
||||
示例 1:
|
||||
输入:n = 4
|
||||
输出:4
|
||||
解释:
|
||||
T_3 = 0 + 1 + 1 = 2
|
||||
T_4 = 1 + 1 + 2 = 4
|
||||
|
||||
示例 2:
|
||||
输入:n = 25
|
||||
输出:1389537
|
||||
|
||||
提示:
|
||||
0 <= n <= 37
|
||||
答案保证是一个 32 位整数,即 answer <= 2^31 - 1。
|
||||
```
|
||||
|
||||
### 题目分析:
|
||||
要是之前有接触过斐波那契数列的话,这道题是非常容易有解决思路的。我们有以下三种方法(正经方法两种,哈哈哈)来解决该问题:
|
||||
|
||||
```
|
||||
1.递归(但是leetcode中是无法AC的,超出时间限制,但是还是会将代码展示出来)
|
||||
2.动态规划(这种题都是已知前面的来求得未知的,使用dp再合适不过)
|
||||
3.暴力(抖机灵,看一乐就可以啦)
|
||||
```
|
||||
|
||||
### GIF动画演示:
|
||||
|
||||

|
||||
|
||||
## 代码:
|
||||
|
||||
### 递归版本:
|
||||
|
||||
```java
|
||||
public int tribonacci(int n) {
|
||||
if (n == 0) {
|
||||
return 0;
|
||||
}
|
||||
if (n == 1 || n == 2) {
|
||||
return 1;
|
||||
}
|
||||
return tribonacci(n - 1) + tribonacci(n - 2) + tribonacci(n -3);
|
||||
}
|
||||
```
|
||||
|
||||
### 动态规划
|
||||
|
||||
```java
|
||||
int[] dp = new int[38];
|
||||
public int tribonacci(int n) {
|
||||
if (dp[n] != 0) {
|
||||
return dp[n];
|
||||
}
|
||||
if (n == 0) {
|
||||
return 0;
|
||||
} else if (n == 1 || n == 2) {
|
||||
return 1;
|
||||
} else {
|
||||
int res = tribonacci(n - 1) + tribonacci(n - 2) + tribonacci(n - 3);
|
||||
dp[n] = res;
|
||||
return res;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### 暴力法(十分暴力,哈哈哈哈……)
|
||||
|
||||
```java
|
||||
public int tribonacci(int n) {
|
||||
int[] Ts = {0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, 121415, 223317, 410744, 755476, 1389537, 2555757, 4700770, 8646064, 15902591, 29249425, 53798080, 98950096, 181997601, 334745777, 615693474, 1132436852, 2082876103};
|
||||
return Ts[n];
|
||||
}
|
||||
```
|
||||
|
||||
@ -0,0 +1,68 @@
|
||||
### 题目描述
|
||||
|
||||
给你一个整数 `n`,请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。
|
||||
|
||||
示例 1:
|
||||
|
||||
```
|
||||
输入:n = 234
|
||||
输出:15
|
||||
解释:
|
||||
各位数之积 = 2 * 3 * 4 = 24
|
||||
各位数之和 = 2 + 3 + 4 = 9
|
||||
结果 = 24 - 9 = 15
|
||||
```
|
||||
|
||||
示例 2:
|
||||
|
||||
```
|
||||
输入:n = 4421
|
||||
输出:21
|
||||
解释:
|
||||
各位数之积 = 4 * 4 * 2 * 1 = 32
|
||||
各位数之和 = 4 + 4 + 2 + 1 = 11
|
||||
结果 = 32 - 11 = 21
|
||||
```
|
||||
|
||||
**提示:**
|
||||
|
||||
```
|
||||
1 <= n <= 10^5
|
||||
```
|
||||
|
||||
### 题目解析
|
||||
|
||||
1、通过取模运算遍历数字每一位
|
||||
|
||||
2、通过两个变量在遍历过程中分别记录求和与求积
|
||||
|
||||
### 动画理解
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
### 参考代码
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int subtractProductAndSum(int n) {
|
||||
int addResult = 0, mulResult = 1;
|
||||
while (n > 0) {
|
||||
int num = n % 10;
|
||||
n /= 10;
|
||||
addResult += num;
|
||||
mulResult *= num;
|
||||
}
|
||||
return mulResult - addResult;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### 复杂度分析
|
||||
|
||||
时间复杂度:O(logN)
|
||||
|
||||
空间复杂度:O(1)
|
||||
@ -0,0 +1,178 @@
|
||||
# 1351. 统计有序矩阵中的负数
|
||||
|
||||
> 本文首发于公众号「图解面试算法」,是 [图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>) 系列文章之一。
|
||||
>
|
||||
> 同步博客:https://www.algomooc.com
|
||||
|
||||
题目来源于 LeetCode 上 1531 题。
|
||||
|
||||
## 题目
|
||||
|
||||
给你一个 m * n 的矩阵 grid,矩阵中的元素无论是按行还是按列,都以非递增顺序排列。
|
||||
|
||||
请你统计并返回 grid 中 负数 的数目。
|
||||
|
||||
|
||||
示例 1:
|
||||
|
||||
|
||||
```
|
||||
输入:grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
|
||||
输出:8
|
||||
解释:矩阵中共有 8 个负数。
|
||||
|
||||
```
|
||||
|
||||
示例 2:
|
||||
|
||||
```
|
||||
输入:grid = [[3,2],[1,0]]
|
||||
输出:0
|
||||
```
|
||||
|
||||
示例 3:
|
||||
|
||||
```
|
||||
输入:grid = [[1,-1],[-1,-1]]
|
||||
输出:3
|
||||
```
|
||||
|
||||
示例 4:
|
||||
|
||||
|
||||
```
|
||||
输入:grid = [[-1]]
|
||||
输出:1
|
||||
|
||||
```
|
||||
|
||||
|
||||
提示:
|
||||
|
||||
|
||||
m == grid.length
|
||||
|
||||
n == grid[i].length
|
||||
|
||||
1 <= m, n <= 100
|
||||
|
||||
-100 <= grid[i][j] <= 100
|
||||
|
||||
|
||||
## 题目解析
|
||||
|
||||
首先审题,在一个矩阵中找出所有负数,这个很好理解,小白一开始做,可以直接暴力遍历,然后依次判断当前值是不是小于0,小于0计数加一。如果是面试的话,面试官一般都会问还没有其他办法,这时候你肯定要说怎么没有,所以我们做一道题不能仅仅限于做出了,要从多方面下手,使得复杂度越小越好。
|
||||
|
||||
所以我们要仔细审题,我们看到题目中有这样一句描述**矩阵中的元素无论是按行还是按列,都以非递增顺序排列**,这句话信息量很大,你品,你仔细品。
|
||||
|
||||
首先我们可以理解到的是:一个 m * n 的矩阵 grid,grid[i][j]<0的话,i那一行第j个到数组最后一个都是小于0,第i行开始,j到后面的列都是小于0
|
||||
|
||||
我们举个例子
|
||||
|
||||
```
|
||||
[
|
||||
[4, 3, -1, -1],
|
||||
[3, 2, -1, -1],
|
||||
[1, 1, -1, -2],
|
||||
[-1, -1, -2, -3]
|
||||
]
|
||||
|
||||
```
|
||||
|
||||
可以看到第一行第三列的值小于0,那么第一行及后面几行的第三列和后面的列的值都小于0。
|
||||
|
||||
所以我们可以进行倒序遍历,找到负数的左边界,也就是左边第一个为负数的值。
|
||||
|
||||
i为行遍历的指针,j为列遍历指针,count为负数的个数,len1为**当前行**的个数,len2为**当前列**的个数
|
||||
|
||||
```
|
||||
初始值
|
||||
let count = 0;
|
||||
let len1 = grid.length
|
||||
let len2 = grid[0].length
|
||||
let i = 0;
|
||||
let j = len2 - 1;
|
||||
```
|
||||
|
||||
然后我们倒序遍历列,行还是正序遍历,以上面的例子来说,我们找到的第一个负数是grid[0][2],然后我们能确定的负数就有如下,所以我们count就可以加上(len1 - i -1) * (len2 - j )
|
||||
|
||||
```
|
||||
[
|
||||
[ -1, -1],
|
||||
[ -1, -1],
|
||||
[ -1, -2],
|
||||
[ -2, -3]
|
||||
]
|
||||
|
||||
```
|
||||
|
||||
然后我们遍历的矩阵就变成如下,然后重复上面操作。
|
||||
|
||||
|
||||
```
|
||||
[
|
||||
[3, 2],
|
||||
[1, 1],
|
||||
[-1, -1]
|
||||
]
|
||||
|
||||
```
|
||||
|
||||
所以我们每次遍历后要更新len1和len2,具体看代码和动画。
|
||||
|
||||
|
||||
## 动画理解
|
||||
|
||||
|
||||
<video id="video" controls="" preload="none" >
|
||||
<source id="mp4" src="../Animation/1351.mp4" type="video/mp4">
|
||||
</video>
|
||||
|
||||
## 参考代码
|
||||
|
||||
```JavaScript
|
||||
/**
|
||||
* @param {number[][]} arr
|
||||
* @return {number}
|
||||
*/
|
||||
var countNegatives = function(arr) {
|
||||
if (arr.length <= 0 ) {return 0}
|
||||
let count = 0;
|
||||
let len1 = arr.length;
|
||||
let len2 = arr[0].length;
|
||||
let i = 0;
|
||||
let j = len2 - 1;
|
||||
while(i < len1) {
|
||||
while(j >= 0) {
|
||||
if (arr[i][j] < 0) {
|
||||
if (j==0){
|
||||
count += (len2 * (len1 - i))
|
||||
len2 = 0
|
||||
break
|
||||
}
|
||||
j--
|
||||
}else {
|
||||
if (len2 == j + 1) {
|
||||
break
|
||||
}
|
||||
count += ((len2 - j - 1) * (len1 - i))
|
||||
len2 = j + 1
|
||||
break
|
||||
}
|
||||
}
|
||||
i++
|
||||
j= len2 - 1
|
||||
}
|
||||
return count
|
||||
};
|
||||
```
|
||||
|
||||
## 复杂度分析
|
||||
|
||||
时间复杂度: O(mn)。 因为如果矩阵中所有的数都为正数,那么要遍历整个矩阵,所以时间复杂度是O(mn)。
|
||||
|
||||
|
||||
空间复杂度:O(1)。
|
||||
|
||||
|
||||

|
||||