mirror of
https://gitee.com/TheAlgorithms/LeetCodeAnimation.git
synced 2024-12-31 15:25:33 +08:00
135 lines
5.5 KiB
Java
135 lines
5.5 KiB
Java
# LeetCode 第 877 号问题:石子游戏
|
||
|
||
> 本文首发于公众号「五分钟学算法」,是[图解 LeetCode ](<https://github.com/MisterBooo/LeetCodeAnimation>)系列文章之一。
|
||
>
|
||
> 个人网站:[https://www.cxyxiaowu.com](https://www.cxyxiaowu.com)
|
||
|
||
### 题目描述
|
||
|
||
喜羊羊和灰太狼用几堆石子在做游戏。偶数堆石子**排成一行**,每堆都有正整数颗石子 `piles[i]` 。
|
||
|
||
游戏以谁手中的石子最多来决出胜负。石子的总数是奇数,所以没有平局。
|
||
|
||
喜羊羊和灰太狼轮流进行,喜羊羊先开始。 每回合,玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止,此时手中石子最多的玩家获胜。
|
||
|
||
假设喜羊羊和灰太狼都发挥出最佳水平,当喜羊羊赢得比赛时返回 `true` ,当灰太狼赢得比赛时返回 `false` 。
|
||
|
||
### 题目分析
|
||
|
||
举两个例子来帮助理解题意。
|
||
|
||
#### 例子一:
|
||
|
||
输入:[ 5,3,4,5 ]
|
||
|
||
输出:true
|
||
|
||
**解释**:
|
||
|
||
喜羊羊先开始,只能拿前 5 颗或后 5 颗石子 。
|
||
|
||
假设他取了前 5 颗,这一行就变成了 [ 3 ,4,5 ] 。
|
||
|
||
如果灰太狼拿走前 3 颗,那么剩下的是 [ 4,5 ],喜羊羊拿走后 5 颗赢得 10 分。
|
||
|
||
如果灰太狼拿走后 5 颗,那么剩下的是 [ 3,4 ],喜羊羊拿走后 4 颗赢得 9 分。
|
||
|
||
这表明,取前 5 颗石子对喜羊羊来说是一个胜利的举动,所以我们返回 true 。
|
||
|
||
|
||
|
||
|
||
|
||
#### 例子二:
|
||
|
||
输入:[ 5,10000,2,3 ]
|
||
|
||
输出:true
|
||
|
||
**解释**:
|
||
|
||
喜羊羊先开始,只能拿前 5 颗或后 3 颗石子 。
|
||
|
||
假设他取了后 3 颗,这一行就变成了 [ 5,10000,2 ]。
|
||
|
||
灰太狼肯定会在剩下的这一行中取走前 5 颗,这一行就变成了 [ 10000,2 ]。
|
||
|
||
然后喜羊羊取走前 10000 颗,总共赢得 10003 分,灰太狼赢得 7 分。
|
||
|
||
这表明,取后 3 颗石子对喜羊羊来说是一个胜利的举动,所以我们返回 true 。
|
||
|
||
**这个例子表明,并不是需要每次都挑选最大的那堆石头**。
|
||
|
||
|
||
|
||
### 题目回答
|
||
|
||
涉及到最优解的问题,那么肯定要去尝试一下使用 **动态规划 **来解决了。
|
||
|
||
先看一下力扣的正规题解:
|
||
|
||
让我们改变游戏规则,使得每当灰太狼得分时,都会从喜羊羊的分数中扣除。
|
||
|
||
令 `dp(i, j)` 为喜羊羊可以获得的最大分数,其中剩下的堆中的石子数是 `piles[i], piles[i+1], ..., piles[j]`。这在比分游戏中很自然:我们想知道游戏中每个位置的值。
|
||
|
||
我们可以根据 `dp(i + 1,j)` 和 `dp(i,j-1)` 来制定 `dp(i,j)` 的递归,我们可以使用动态编程以不重复这个递归中的工作。(该方法可以输出正确的答案,因为状态形成一个DAG(有向无环图)。)
|
||
|
||
当剩下的堆的石子数是 `piles[i], piles[i+1], ..., piles[j]` 时,轮到的玩家最多有 2 种行为。
|
||
|
||
可以通过比较 `j-i`和 `N modulo 2` 来找出轮到的人。
|
||
|
||
如果玩家是喜羊羊,那么它将取走 `piles[i]` 或 `piles[j]` 颗石子,增加它的分数。之后,总分为 `piles[i] + dp(i+1, j)` 或 `piles[j] + dp(i, j-1)`;我们想要其中的最大可能得分。
|
||
|
||
如果玩家是灰太狼,那么它将取走 `piles[i]` 或 `piles[j]` 颗石子,减少喜羊羊这一数量的分数。之后,总分为 `-piles[i] + dp(i+1, j)` 或 `-piles[j] + dp(i, j-1)`;我们想要其中的最小可能得分。
|
||
|
||
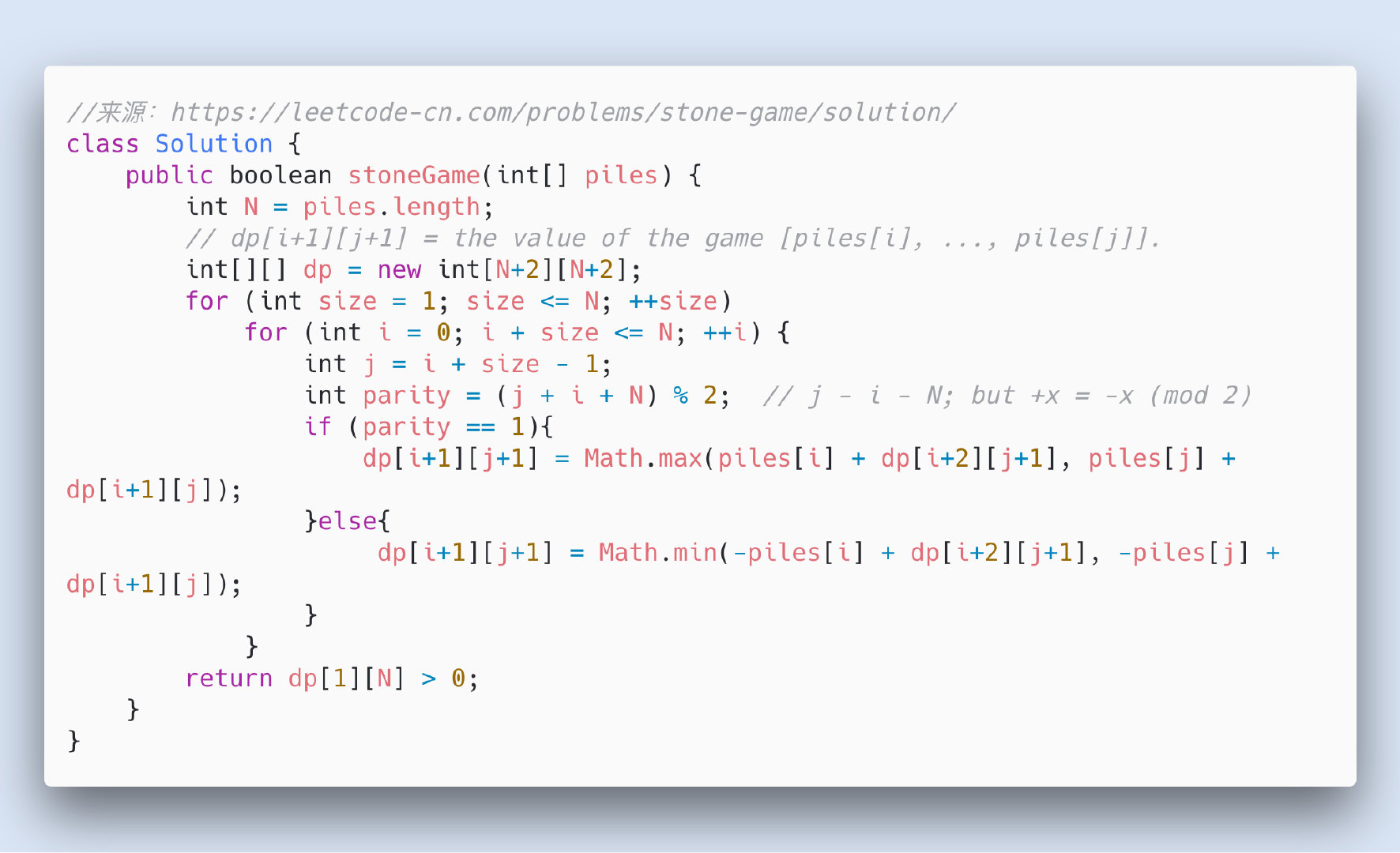
代码如下:
|
||
|
||
|
||
|
||
|
||
|
||
上面的代码并不算复杂,当然,如果你看不懂也没关系,不影响解决问题,请看下面的数学分析。
|
||
|
||
|
||
|
||
### 数学分析
|
||
|
||
因为石头的数量是奇数,因此只有两种结果,输或者赢。
|
||
|
||
喜羊羊先开始拿石头,随便拿!然后比较石头数量:
|
||
|
||
1. 如果石头数量多于对手,赢了;
|
||
2. 如果石头数量少于对手,自己拿石头的顺序和对手拿石头的顺序对调(**因为是偶数堆石头,所以可以全部对调**),还是赢。
|
||
|
||
所以代码如下:
|
||
|
||
```java
|
||
class Solution {
|
||
public boolean stoneGame(int[] piles) {
|
||
return true;
|
||
}
|
||
}
|
||
```
|
||
|
||
下面给给大家介绍一种简单的策略作为参考,使用这种策略可以保证先取石头的喜羊羊一定能够获胜。
|
||
|
||
首先分别计算出序号为奇数和序号为偶数的石头堆中的石头总数,然后进行比较,如果奇数堆石头总数更多则喜羊羊永远保证自己选取奇数石堆,反之则选择偶数。
|
||
|
||
举例来说,假设石堆为 [ 5,10000,2,3 ] ,那么奇数石堆总和为 7(从 1 开始编号),偶数石堆总数为 1003 ,则喜羊羊要保证自己永远选择偶数堆即第四堆和第二堆,就可以取胜。
|
||
|
||
但是这种选择方法得到的**结果未必是最优解**,例如石堆为 [ 2,1,3,5 ] 当使用动态规划确保喜羊羊和灰太狼都选择最优解的时候,喜羊羊会拿走 [ 2,5 ] 两堆棋子,而灰太狼则拿走 [ 1,3 ] 两堆。但是使用这种策略在即使不是最优解的情况下依然可以保证喜羊羊胜利,所以作为先手的喜羊羊必定有方法取得比赛的胜利。
|
||
|
||
看完之后,你的心情是怎么样的?
|
||
|
||
此题的LeetCode 的评论区里一片吐槽:**这是什么沙雕题目!**
|
||
|
||
可能搞过 ACM 等竞赛的人都会微微一笑:不会几万个套路怎么好意思说自己是 acmer 。我们这些普通人为之惊奇的题目,到他们这里就是彻底被玩坏了,各种稀奇古怪的秒解。
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||

|