2.5 KiB
2.5 KiB
散列表
散列表是数组的一种扩展,利用数组下标的随机访问特性。
散列思想
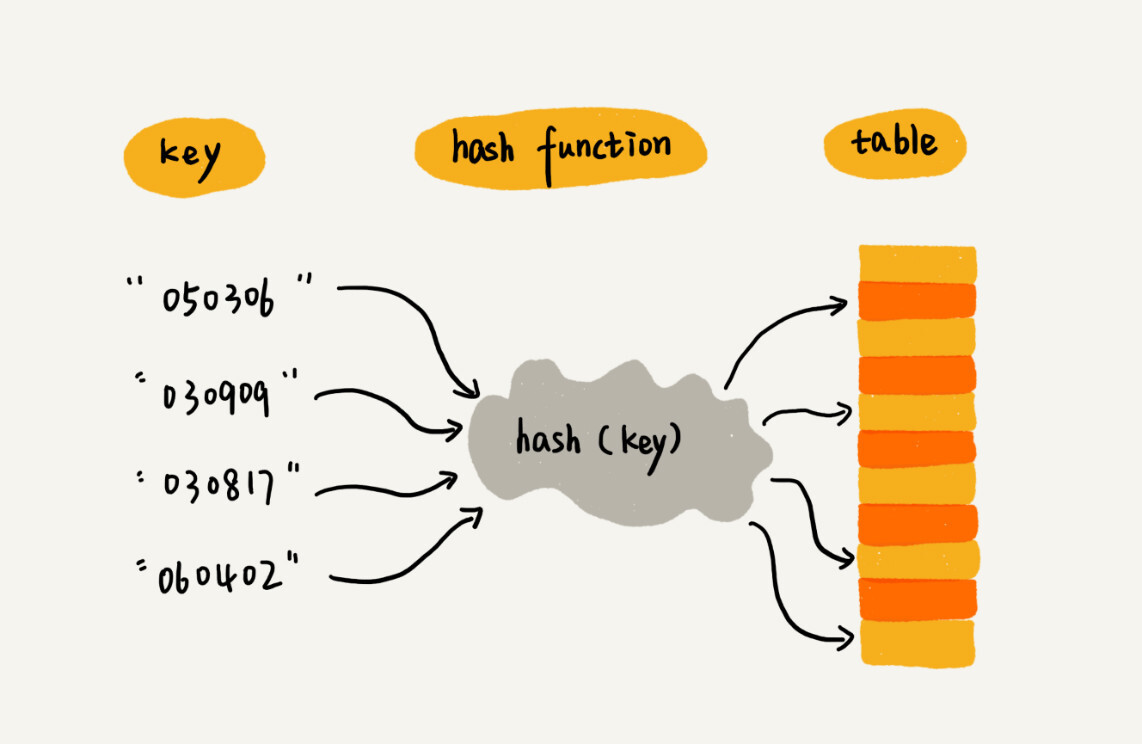
- 键/关键字/Key:用来标识一个数据
- 散列函数/哈希函数/Hash:将 Key 映射到数组下标的函数
- 散列值/哈希值:Key 经过散列函数得到的数值
本质:利用散列函数将关键字映射到数组下标,而后利用数组随机访问时间复杂度为 \Theta(1) 的特性快速访问。
散列函数
- 形式:
hash(key) - 基本要求
- 散列值是非负整数
- 如果
key1 == key2,那么hash(key1) == hash(key2) - 如果
key1 != key2,那么hash(key1) != hash(key2)
第 3 个要求,实际上不可能对任意的 key1 和 key2 都成立。因为通常散列函数的输出范围有限而输入范围无限。
散列冲突
- 散列冲突:
key1 != key2但hash(key1) == hash(key2)
散列冲突会导致不同键值映射到散列表的同一个位置。为此,我们需要解决散列冲突带来的问题。
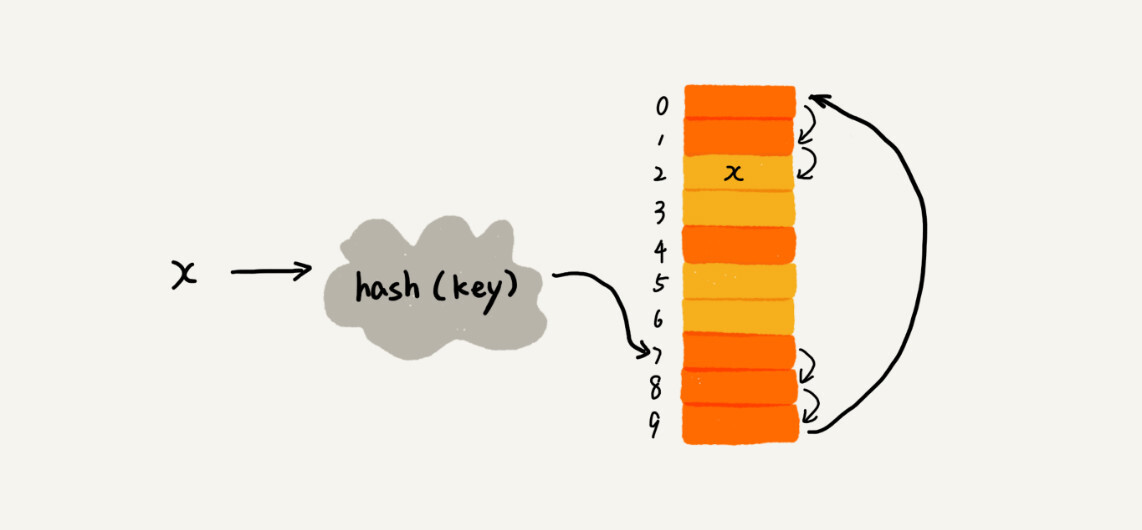
开放寻址法
如果遇到冲突,那就继续寻找下一个空闲的槽位。
线性探测
插入时,如果遇到冲突,那就依次往下寻找下一个空闲的槽位。(橙色表示已被占用的槽位,黄色表示空闲槽位)
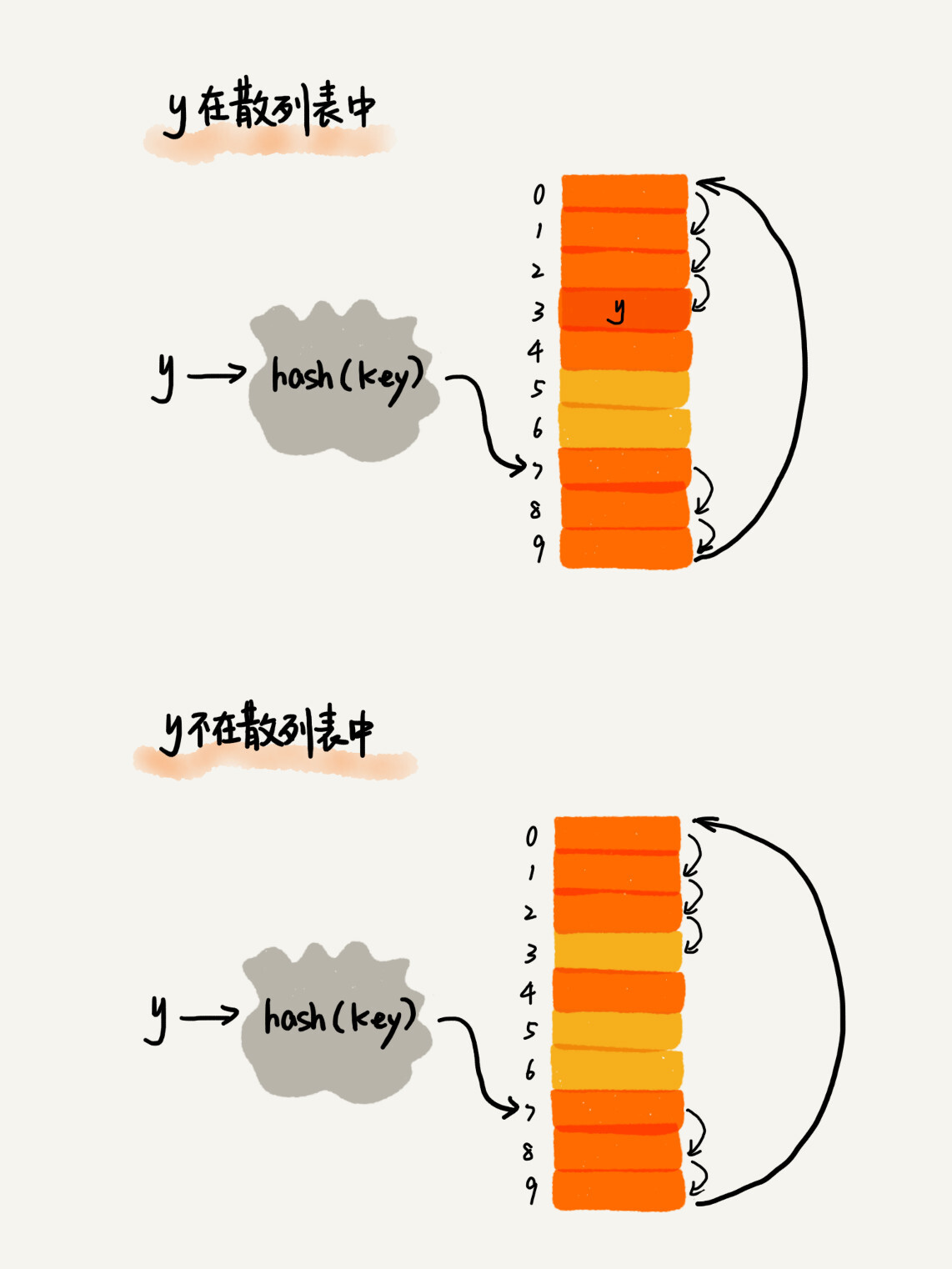
查找时,如果目标槽位上不是目标数据,则依次往下寻找;直至遇见目标数据或空槽位。
删除时,标记为 deleted,而不是直接删除。
平方探测(Quadratic probing)
插入时,如果遇到冲突,那就往后寻找下一个空闲的槽位,其步长为 1^2, 2^2, 3^2, $\ldots$。
查找时,如果目标槽位上不是目标数据,则依次往下寻找,其步长为 1^2, 2^2, 3^2, $\ldots$;直至遇见目标数据或空槽位。
删除时,标记为 deleted,而不是直接删除。
装载因子(load factor)
\text{load factor} = \frac{size()}{capacity()}
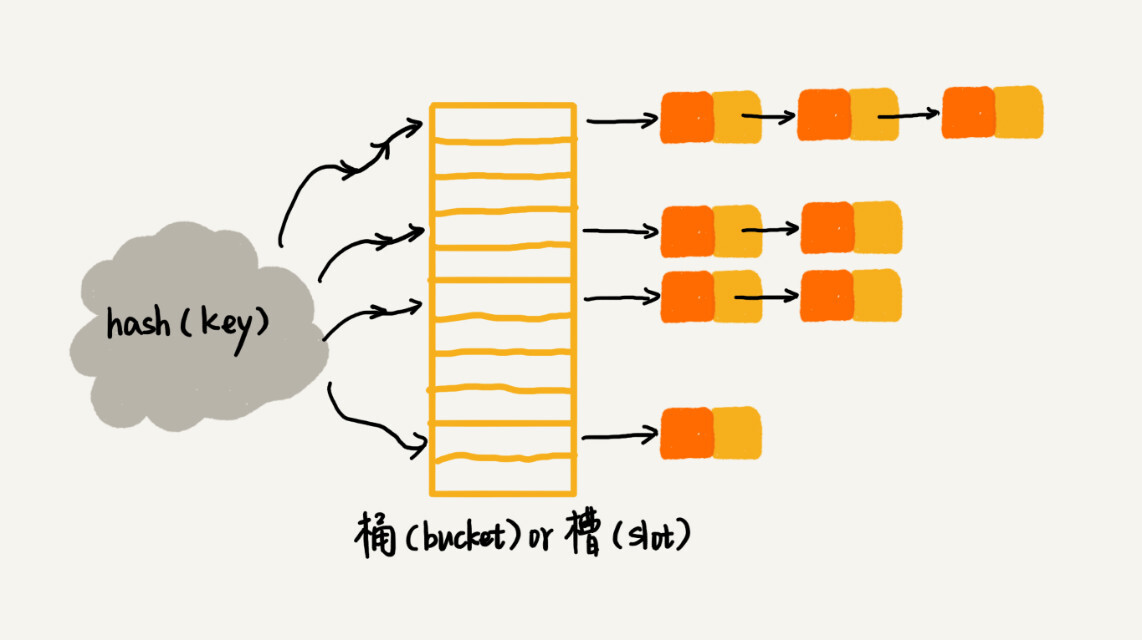
链表法
所有散列值相同的 key 以链表的形式存储在同一个槽位中。
插入时,不论是否有冲突,直接插入目标位置的链表。
查找时,遍历目标位置的链表来查询。
删除时,遍历目标位置的链表来删除。