5.1 KiB
本文首发于公众号「图解面试算法」，是 图解 LeetCode 系列文章之一。
本题选择leetcode中第42题，hard级别，目前通过率50.8%#
题目描述：
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
题目分析：
通过题意，一个“凹槽”可以存储的雨水的容量取决于它前后的柱子。
解法一：
仔细想想，其实这跟木桶原理是有相似的地方的，针对每一个柱子，我们需要往前看和往后看，分别找出当前柱子前面最高的柱子和后面最高的柱子。
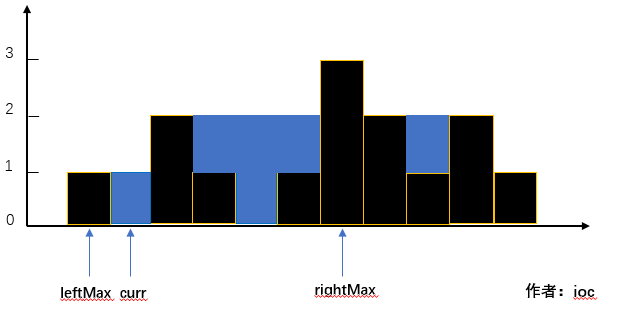
这里有三种情况我们需要了解：
-
当前柱子小于前后两个柱子中最矮的那个
当前位置可以存储的雨水容量 = leftMax - curr = 1
-
当前柱子等于前后两个柱子中最矮的那个
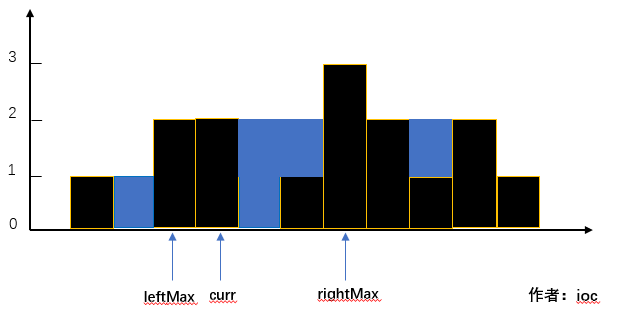
当前位置可以存储的雨水容量为0
-
当前柱子大于前后两个柱子中最矮的那个
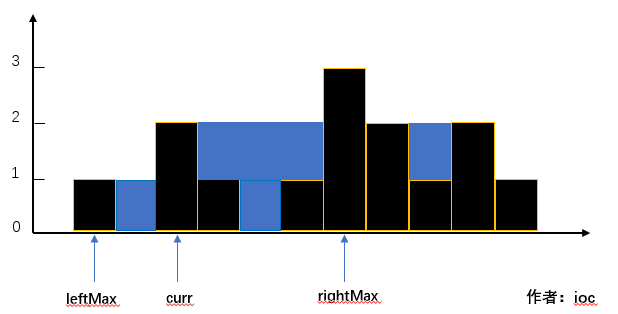
因为curr < leftMax，所以当前位置无法存储雨水
GIF动画演示：
代码：
public int trap02(int[] height) {
int sum = 0;
//最两端的列不用考虑，因为一定不会有水。所以下标从 1 到 length - 2
for (int i = 1; i < height.length - 1; i++) {
int max_left = 0;
//找出左边最高
for (int j = i - 1; j >= 0; j--) {
if (height[j] > max_left) {
max_left = height[j];
}
}
int max_right = 0;
//找出右边最高
for (int j = i + 1; j < height.length; j++) {
if (height[j] > max_right) {
max_right = height[j];
}
}
//找出两端较小的
int min = Math.min(max_left, max_right);
//只有较小的一段大于当前列的高度才会有水，其他情况不会有水
if (min > height[i]) {
sum = sum + (min - height[i]);
}
}
return sum;
}
可以看到，上面方法的时间复杂度达到了O(n^2)
那么有没有更好的办法来解决这个问题？
下面的方法巧妙的使用了双指针来解决问题：
与上述解法的思路大致是相同的，都是单个地求出当前墙可以存储雨水的容量；这种解法也是非常的巧妙，是在浏览解题区的时候碰见的，大佬还做了视频（链接放在文末），讲解的非常清楚，我大概用自己的思路来作一文字叙述：
既然使用的是twoPointers的思路，那么我们需要分别从数组的最前面和最后面开始，这两个指针是互不影响，都是各走各的，但是如何确定当前指针走过的地方能存放多少雨水量呢？
这个时候，我们就需要两块挡板leftMax和rightMax，这两块挡板最开始都是挡在最外面的墙边，随着两个指针前进，leftMax代表的是left走过的路中最高的墙，rightMax同理。
那么如何计算雨水量呢？
比较左右两个挡板的高度，然后根据两个挡板各自的指针配合计算。
- 如果左边挡板的高度小于右边的挡板高度，那么左边指针之前的雨水量取决于leftMax和height[left]的大小关系，如果前者大于后者，那么容量等与前者减去后者；反之，容量为0（可以参考解法一中的图来理解）
- 如果左边挡板的高度大于等于右边挡板的高度，与上一种情况基本相同，只不过是求的右边的雨水量。
- 在每次移动指针之后，我们要将挡板更新到最大值。
其实道理也是比较简单，用宏观的思维去看待整个问题，最起码先保证两边的墙的高度（两块挡板），然后依次去到其中各个墙之间能装多少雨水的问题上。（求每次更新最高的挡板和指针指向的墙之间可以存储的雨水量）
代码：
public int trap(int[] height) {
if (height.length == 0) return 0;
int left = 0;
int right = height.length-1;
int leftMax = 0;
int rightMax = 0;
int result = 0;
while (left <= right) {
if (leftMax < rightMax) {
result += leftMax - height[left] > 0 ?
leftMax - height[left] : 0;
leftMax = Math.max(leftMax, height[left]);
left++;
} else {
result += rightMax - height[right] > 0 ?
rightMax - height[right] : 0;
rightMax = Math.max(rightMax, height[right]);
right--;
}
}
return result;
}
时间复杂度：O(n) 空间复杂度：O(1)