44 lines
3.3 KiB
Markdown
44 lines
3.3 KiB
Markdown
# 跳表(Skip List)
|
||
|
||
支持快速地:
|
||
|
||
* 插入
|
||
* 删除
|
||
* 查找
|
||
|
||
某些情况下,跳表甚至可以替代红黑树(Red-Black tree)。Redis 当中的有序集合(Sorted Set)是用跳表实现的。
|
||
|
||
## 跳表的结构
|
||
|
||
跳表是对链表的改进。对于单链表来说,即使内容是有序的,查找具体某个元素的时间复杂度也要达到 $O(n)$。对于二分查找来说,由于链表不支持随机访问,根据 `first` 和 `last` 确定 `cut` 时,必须沿着链表依次迭代 `std::distance(first, last) / 2` 步;特别地,计算 `std::(first, last)` 本身,就必须沿着链表迭代才行。此时,二分查找的效率甚至退化到了 $O(n \log n)$,甚至还不如顺序遍历。
|
||
|
||
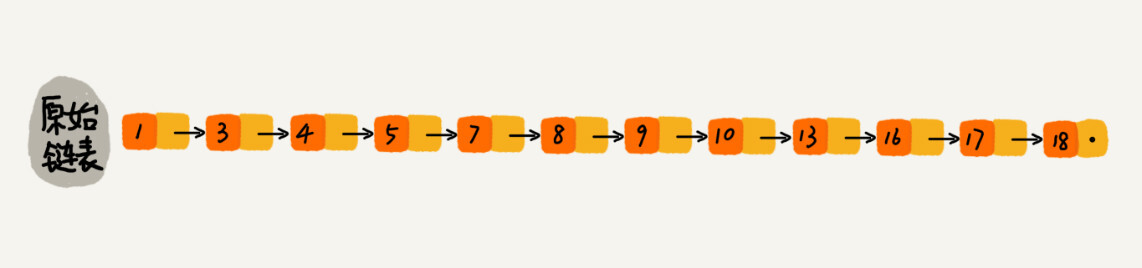
|
||
|
||
跳表的核心思想是用空间换时间,构建足够多级数的索引,来缩短查找具体值的时间开销。
|
||
|
||
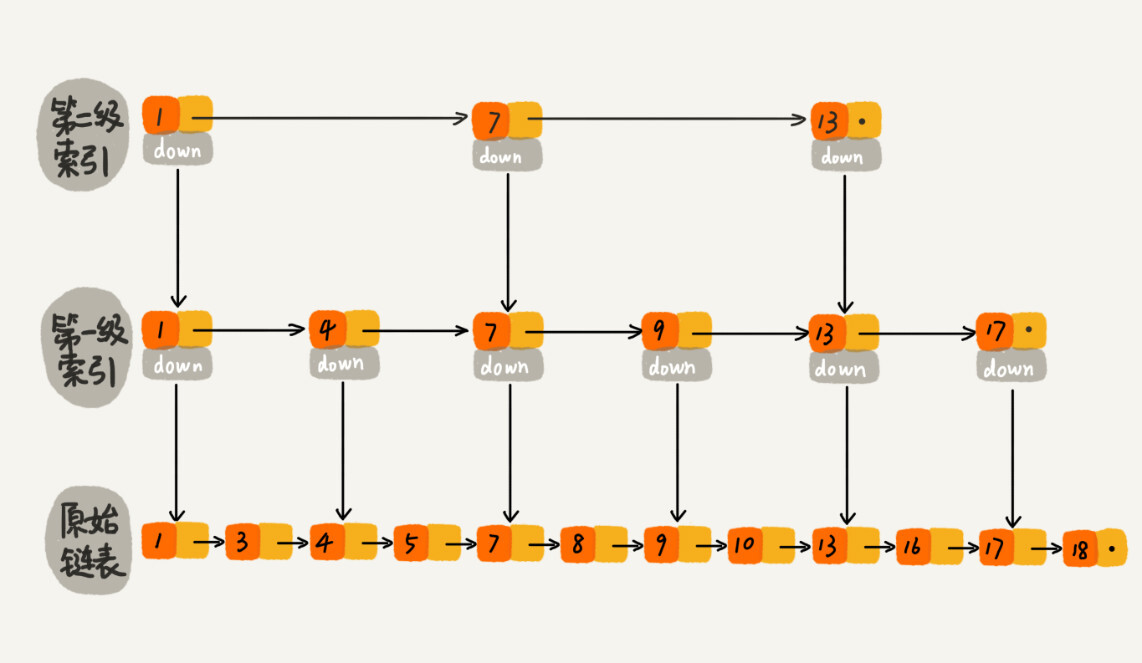
|
||
|
||
例如对于一个具有 64 个有序元素的五级跳表,查找起来的过程大约如下图所示。
|
||
|
||
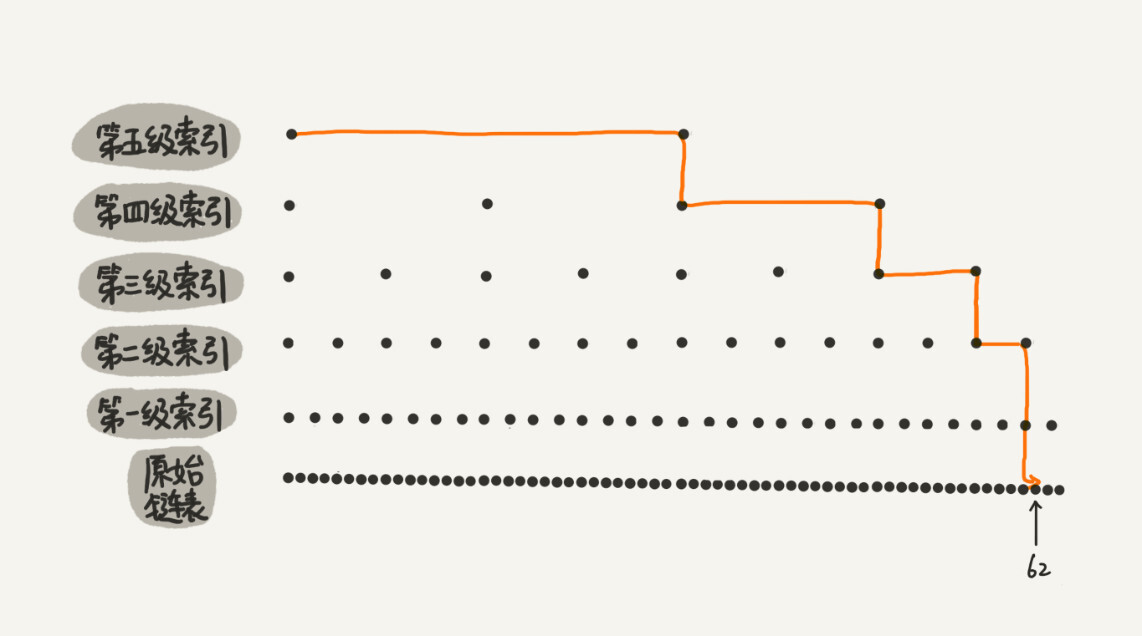
|
||
|
||
## 复杂度分析
|
||
|
||
对于一个每一级索引的跨度是下一级索引 $k$ 倍的跳表,每一次 `down` 操作,相当于将搜索范围缩小到「剩余的可能性的 $1 / k$」。因此,查找具体某个元素的时间复杂度大约需要 $\lfloor \log_k n\rfloor + 1$ 次操作;也就是说时间复杂度是 $O(\log n)$。
|
||
|
||
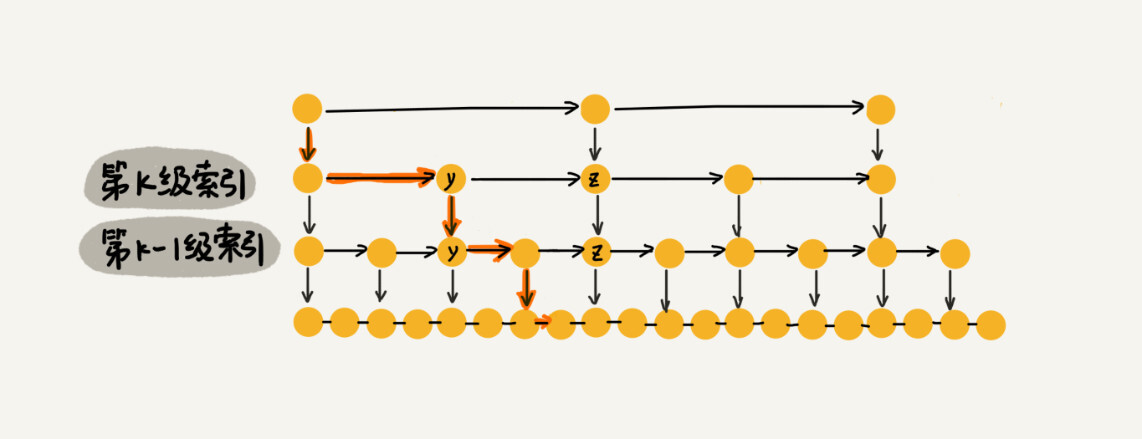
|
||
|
||
前面说了,跳表是一种用空间换时间的数据结构。因此它的空间复杂度一定不小。我们考虑原链表有 $n$ 个元素,那么第一级索引就有 $n / k$ 个元素,剩余的索引依次有 $n / k^2$, $n / k^3$, ..., $1$ 个元素。总共的元素个数是一个等比数列求和问题,它的值是 $\frac{n - 1}{k - 1}$。可见,不论 $k$ 是多少,跳表的空间复杂度都是 $O(n)$;但随着 $k$ 的增加,实际需要的额外节点数会下降。
|
||
|
||
## 高效地插入和删除
|
||
|
||
对于链表来说,插入或删除一个给定结点的时间复杂度是 $O(1)$。因此,对于跳表来说,插入或删除某个结点,其时间复杂度完全依赖于查找这类结点的耗时。而我们知道,在跳表中查找某个元素的时间复杂度是 $O(\log n)$。因此,在跳表中插入或删除某个结点的时间复杂度是 $O(\log n)$。
|
||
|
||
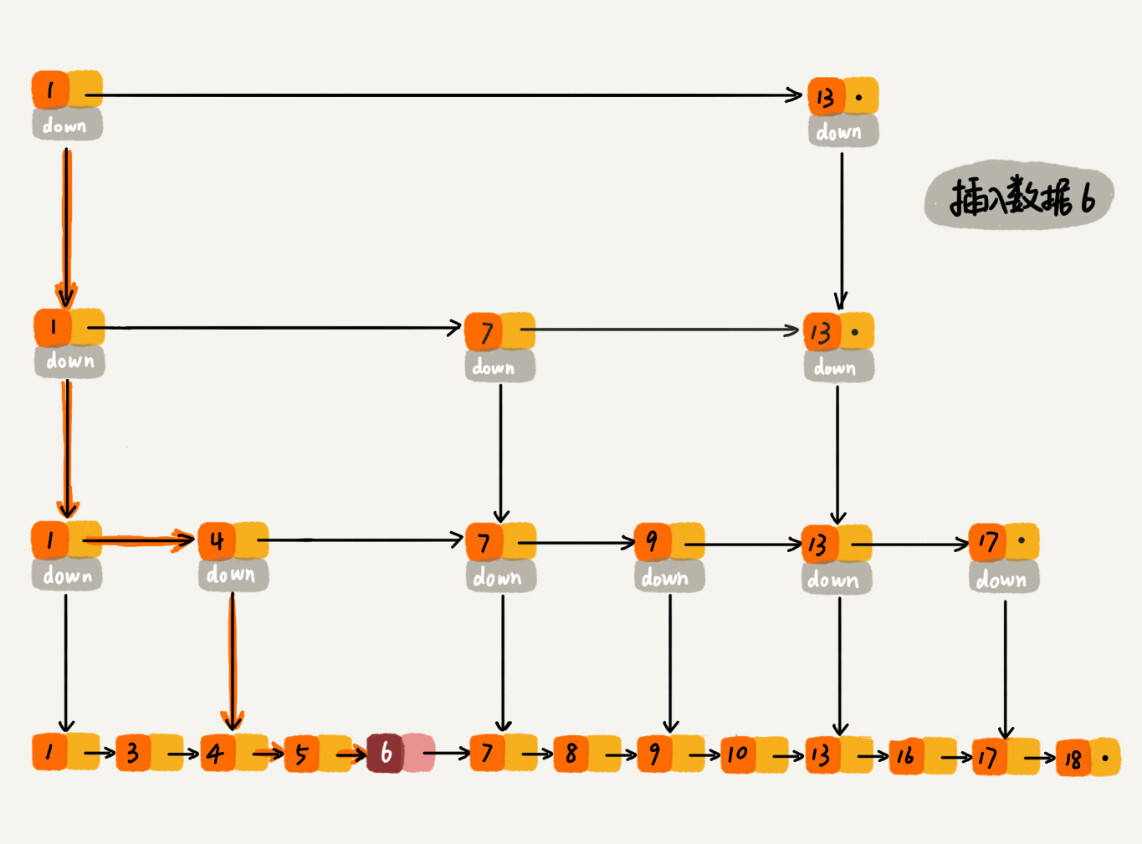
|
||
|
||
## 跳表索引的动态更新
|
||
|
||
为了维护跳表的结构,在不断插入数据的过程中,有必要动态维护跳表的索引结构。一般来说,可以采用随机层级法。具体来说是引入一个输出整数的随机函数。当随机函数输出 $K$,则更新从第 $1$ 级至第 $K$ 级的索引。为了保证索引结构和数据规模大小的匹配,一般采用二项分布的随机函数。
|
||
|
||
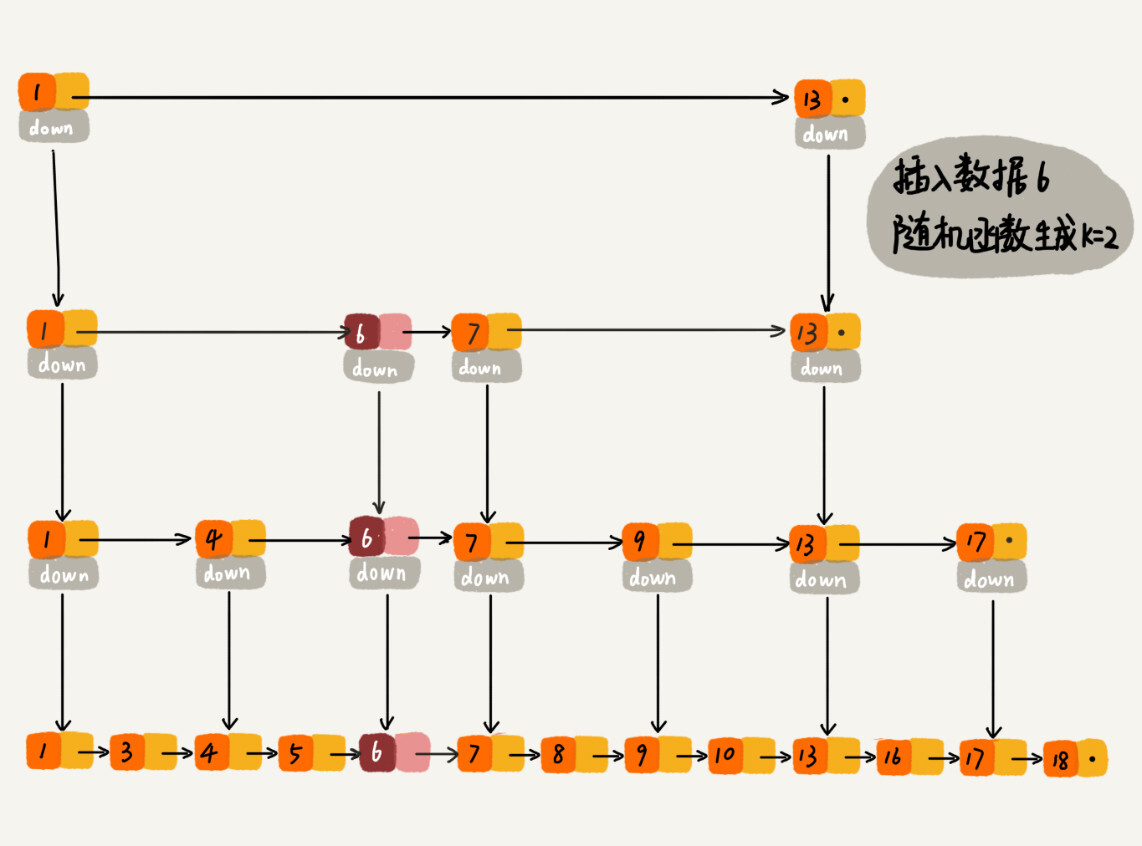
|